ਸਮਤਾ: ਰੀਵਿਜ਼ਨਾਂ ਵਿਚ ਫ਼ਰਕ

Browse history interactively

← ਪੁਰਾਣੀ ਤਬਦੀਲੀ ਅਗਲੀ ਸੋਧ →

ਸਮੱਗਰੀ ਮਿਟਾਈ ਸਮੱਗਰੀ ਜੋੜੀ

VisualWikitext

ਇਨਲਾਈਨ

04:22, 17 ਦਸੰਬਰ 2015 ਦਾ ਦੁਹਰਾਅ

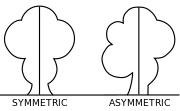
ਇੱਕ ਫ੍ਰੈਕਟਲ- ਵਰਗਾ ਅਕਾਰ ਜੋ ਸਮਰੂਪਤਾ ਦੀਆਂ ਤਿੰਨ ਕਿਸਮਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਰਿਫਲੈਕਸ਼ਨਲ ਸਮਰੂਪਤਾ, ਰੋਟੇਸ਼ਨਲ ਸਮਰੂਪਤਾ ਅਤੇ ਸਵੈ-ਸਮਾਨਤਾ ਰੱਖਦਾ ਹੈ। ਇਹ ਅਕਾਰ ਇੱਕ ਸੀਮਤ ਉਪਵੰਡ ਕਨੂੰਨ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਕੀਤੀ ਗਈ ਹੈ

ਸਮਿੱਟਰੀ (ਗ੍ਰੀਕ ਤੋਂ συμμετρία symmetria ਜਿਸਦਾ ਅਰਥ ਹੈ “ਅਯਾਮਾਂ, ਉਚਿਤ ਅਨੁਪਾਤ, ਵਿਵਸਥਾ ਵਿੱਚ ਸਹਿਮਤੀ”) ਰੋਜ਼ਾਨਾ ਜਿੰਦਗੀ ਦੀ ਭਾਸ਼ਾ ਵਿੱਚ ਲੈਅਬੱਧਤਾ ਪ੍ਰਤਿ ਇੱਕ ਸਮਝ ਅਤੇ ਸੁੰਦਰ ਅਨੁਪਾਤ ਅਤੇ ਸੰਤੁਲਨ ਹੁੰਦਾ ਹੈ। ਗਣਿਤ ਵਿੱਚ, ਸਮਰੂਪਤਾ ਦੀ ਪਰਿਭਾਸ਼ਾ ਹੋਰ ਸ਼ੁੱਧ ਪਰਿਭਾਸ਼ਾ ਹੁੰਦੀ ਹੈ, ਕਿ ਕੋਈ ਵਸਤੂ ਕਿਸੇ ਪਰਿਵਰਤਨ ਪ੍ਰਤਿ ਸਥਿਰ ਰਹਿੰਦੀ ਹੈ, ਜਿਵੇਂ ਰਿਫਲੈਕਸ਼ਨ ਪਰ ਹੋਰ ਪਰਿਵਰਤਨਾਂ ਸਮੇਤ ਵੀ । ਭਾਵੇਂ ਸਮਰੂਪਤਾ ਦੇ ਇਹ ਦੋ ਅਰਥ ਕਦੇ ਕਦੇ ਵੱਖਰੇ ਤੌਰ ਤੇ ਦੱਸੇ ਜਾਂਦੇ ਹਨ, ਫੇਰ ਵੀ ਇਹ ਸਬੰਧਤ ਹੁੰਦੇ ਹਨ, ਇਸਲਈ ਇਹ ਇੱਥੇ ਇਕੱਠੇ ਚਰਚਿਤ ਕੀਤੇ ਗਏ ਹਨ।

ਗਣਿਤਿਕ ਸਮਰੂਪਤਾ ਨੂੰ, ਰੇਖਾਗਣਿਤਿਕ ਪਰਿਵਰਤਨਾਂ ਜਿਵੇਂ ਸਕੇਲਿੰਗ, ਰਿਫਲੈਕਸ਼ਨ, ਅਤੇ ਰੋਟੇਸ਼ਨ ਰਾਹੀਂ; ਫੰਕਸ਼ਨਲ ਪਰਿਵਰਤਨਾਂ ਦੀਆਂ ਹੋਰ ਕਿਸਮਾਂ ਰਾਹੀਂ; ਅਤੇ ਅਮੂਰਤ ਵਸਤੂਆਂ, ਸਿਧਾਂਤਕ ਮਾਡਲਾਂ, ਭਾਸ਼ਾ, ਸੰਗੀਤ, ਅਤੇ ਇੱਥੋਂ ਤੱਕ ਕਿ ਖੁਦ ਗਿਆਨ ਰਾਹੀਂ; ਕਿਸੇ ਸਥਾਨਿਕ ਸਬੰਧ ਦੇ ਰੂਪ ਵਿੱਚ, ਵਕਤ ਦੇ ਲਾਂਘੇ ਨਾਲ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ।

ਇਹ ਆਰਟੀਕਲ ਸਮਰੂਪਤਾ ਨੂੰ ਤਿੰਨ ਦ੍ਰਿਸ਼ਟੀਕੋਣਾਂ ਤੋਂ ਦਰਸਾਉਂਦਾ ਹੈ: ਗਣਿਤ ਵਿੱਚ, ਰੇਖਾਗਣਿਤ ਸਮੇਤ, ਬਹੁਤ ਸਾਰੇ ਲੋਕਾਂ ਲਈ ਸਮਰੂਪਤਾ ਦੀ ਸਭ ਤੋਂ ਜਿਆਦਾ ਪ੍ਰਸਿੱਧ ਕਿਸਮ; ਵਿਗਿਆਨ ਅਤੇ ਕੁਦਰਤ ਵਿੱਚ; ਅਤੇ ਕਲਾ ਵਿੱਚ, ਜਿਸ ਵਿੱਚ ਆਰਕੀਟੈਕਚਰ, ਕਲਾ, ਅਤੇ ਸੰਗੀਤ ਸ਼ਾਮਿਲ ਹਨ।

ਸਮਰੂਪਤਾ ਦਾ ਉਲਟ ਅਸਮਰੂਪਤਾ ਹੁੰਦੀ ਹੈ।

ਗਣਿਤ ਵਿੱਚ

ਕੋਉ ਵੀ ਰੇਖਾ ਗਣਿਤ ਦੀ ਸਕਲ, ਜਾਂ ਵਸਤੂ ਵਿਚ ਸਮਤਾ ਹੈ ਜੇ ਇਸ ਨੂੰ ਦੋ ਜਾਂ ਦੋ ਤੋਂ ਵੱਧ ਬਰਾਬਰ ਹਿੱਸਿਆ ਵਿੱਚ ਵੰਡੀ ਜਾਵੇ

ਜੇ ਕਿਸੇ ਇਕ ਰੇਖਾ ਨਾਲ ਕੋਈ ਵਸਤੁ ਨੂੰ ਵੱਖ ਕਰੇ ਤੇ ਦੋਨੋ ਇਕ ਦੂਜੇ ਦਾ ਪ੍ਰਤੀਬਿੰਬ ਹੋਣ ਤਾਂ ਇਸ ਸਮਤਾ ਨੂੰ ਪ੍ਰਤੀਬਿੰਬ ਸਮਤਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਜੇ ਕਿਸੇ ਵਸਤੂ ਨੂੰ ਇਸ ਦੀ ਸਕਲ ਨੂੰ ਨਾ ਬਦਲ ਕੇ ਕਿਸੇ ਖ਼ਾਸ ਬਿੰਦੂ ਤੇ ਘੁਮਾਇਆ ਜਾ ਸਕਦਾ ਹੋਵੇ ਤਾਂ ਇਸ ਸਮਤਾ ਨੂੰ ਰੋਟੇਸ਼ਨਲ ਸਮਤਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਜੇ ਕੋਈ ਵਸਤੂ ਫੈਲਣ ਨਾਲ ਆਪਣੀ ਮੁਢਲੀ ਸ਼ਕਲ ਨਾ ਬਦਲੇ ਤਾਂ ਇਸ ਸਮਤਾ ਨੂੰ ਸਕੇਲ ਸਮਤਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।

ਰੇਖਾਗਣਿਤ ਵਿੱਚ

ਸਮਰੂਪ ਦੋ ਵਸਤੂਆਂ ਇਕੋ ਹੀ ਸ਼ਕਲ, ਅਕਾਰ ਦੀਆਂ ਹੋਣ ਉਸ ਨੂੰ ਸਮਰੂਪ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇੱਕ ਵਸਤੂ ਨੂੰ ਦੂਜੀ ਤੋਂ ਉਸ ਦੀਆਂ ਭੁਜਾਵਾਂ ਨੂੰ ਅਨੁਪਾਤਿਕ ਵਧਾਕੇ ਜਾਂ ਘਟਾਕੇ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਜਿਵੇ ਸਾਰੇ ਚੱਕਰ ਇੱਕ ਦੂਜੇ ਨੂੰ ਸਮਰੂਪ ਹੁੰਦੇ ਹਨ। ਸਾਰੀਆਂ ਸਮਬਾਹੂ ਤ੍ਰਿਭੁਜ ਸਮਰੂਪ ਹੁੰਦੀਆਂ ਹਨ। ਪਰ ਆਇਤ, ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਅਤੇ ਅੰਡਾਕਾਰ ਸਮਰੂਪ ਨਹੀਂ ਹੁੰਦੇ। ਜੇ ਕਿਸੇ ਤ੍ਰਿਭੁਜ ਦੇ ਦੋ ਕੋਣਾਂ ਦੀ ਮਾਤਰਾ ਦੁਜੀ ਤ੍ਰਿਭੁਜ ਦੇ ਦੋ ਕੋਣਾਂ ਦੇ ਬਰਾਬਰ ਹੋਵੇ ਤਾਂ ਤ੍ਰਿਭੁਜ ਸਮਰੂਪ ਹੁੰਦੀਆਂ ਹਨ ਇਸ ਨਿਯਮ ਨੂੰ AAA ਸਮਰੂਪ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ $\triangle ABC$ ਅਤੇ $\triangle A'B'C'$ ਵਿੱਚ ਉਹਨਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਸਮਾਨ ਹੁੰਦੇ ਹਨ। ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਉਹਨਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਵਰਗ ਦੇ ਅਨੁਪਾਤ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।^[1]

ਨਿਯਮ

ਜੇ $\angle BAC$

ਅਤੇ

$\angle B'A'C'$

ਕੋਣਾਂ ਦਾ ਮਾਪ ਅਤੇ

$\angle ABC$

ਅਤੇ

$\angle A'B'C'$

ਦਾ ਮਾਪ ਬਰਾਬਰ ਹੋਵੇ ਤਾਂ ਤੀਜਾ ਕੋਣ

$\angle ACB$

ਅਤੇ

$\angle A'C'B'$

ਬਰਾਬਰ ਹੀ ਹੁੰਦੇ ਹਨ ਤਾਂ ਦੋਨੋ ਤ੍ਰਿਭੁਜ ਸਮਰੂਪ ਹੁੰਦੇ ਹਨ।

\triangle ABC\sim \triangle A'B'C'\,

.

ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਸਾਰੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਇਕੋ ਹੀ ਅਨੁਪਾਤ ਵਿੱਚ ਹੁੰਦੀਆਂ ਹਨ।

{AB \over A'B'}={BC \over B'C'}={AC \over A'C'}

. ਤਾਂ ਤ੍ਰਿਭੁਜਾ ਸਮਰੂਪ ਹਨ।

ਜੇ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਦੋ ਭੁਜਾਵਾਂ ਇਕੋ ਹੀ ਅਨੁਪਾਤ ਵਿੱਚ ਹੋਣ ਅਤੇ ਉਹਨਾਂ ਵਿਚਕਾਰਲਾ ਕੋਣ ਬਰਾਬਰ ਹੋਵੇ ਤਾਂ ਤ੍ਰਿਭੁਜ ਸਮਰੂਪ ਹੁੰਦੇ ਹਨ।

{AB \over A'B'}={BC \over B'C'}

ਅਤੇ

\angle ABC

ਅਤੇ

\angle A'B'C'

ਬਰਾਬਰ ਹਨ।

ਜਦੋ ਦੋ ਤ੍ਰਿਭੁਜ $\triangle ABC$ ਅਤੇ $\triangle A'B'C'$ ਸਮਰੂਪ ਹੋਣ ਤਾਂ ਉਹਨਾਂ ਨੂੰ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ।

\triangle ABC\sim \triangle A'B'C'\,

.

ਤਰਕ ਵਿੱਚ

ਸਬੰਧ R ਸਮਤਾ ਹੈ ਜੇ ਅਤੇ ਸਿਰਫ ਜੇ Rab ਸੱਚ ਹੈ ਤਾਂ Rba ਸੱਚ ਹੈ।.^[2] ਤਦ ਜੇ ਪਾਲ ਦੀ ਉਮਰ ਮੈਰੀ ਜਿਨੀ ਹੈ ਤਾਂ ਮੈਰੀ ਦੀ ਉਮਰ ਪਾਲ ਜਿਨੀ ਹੈ ਤਾਂ ਇਹ ਤਰਕ ਦੀ ਸਮਤਾ ਹੈ। ਇਹ ਸਬੰਧ ਅਤੇ (∧, or &), ਜਾਂ (∨, or |), ਦੂਹਰੀ ਸ਼ਤਰ (ਜੇ ਅਤੇ ਸਿਰਫ ਜੇ) (↔) ਹਨ।

ਗਣਿਤ ਦੇ ਹੋਰ ਖੇਤਰਾਂ ਵਿੱਚ

ਵਿਗਿਆਨ ਅਤੇ ਕੁਦਰਤ ਵਿੱਚ

ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ

ਜੀਵ ਵਿਗਿਆਨ ਵਿੱਚ

ਸਾਰੇ ਪ੍ਰਾਣੀ ਸਮੇਤ ਮਨੁੱਖ ਦਾ ਸੱਜਾ ਪਾਸਾ ਅਤੇ ਖੱਬਾ ਪਾਸੇ ਵਿਚ ਸਮਾਨਤਾ ਹੈ। ਜੇ ਇਹਨਾਂ ਦੀ ਸਰੀਰ ਨੂੰ ਵਿੱਚਕਾਰ ਤੋਂ ਦੇਖਿਆ ਜਾਵੇ ਤਾ ਸੱਜਾ ਅਤੇ ਖੱਬਾ ਵਿਚ ਸਮਤਾ ਹੈ। ਪੌਦਿਆ ਅਤੇ ਸਮੁੰਦਰੀ ਜੀਵਾਂ ਵਿੱਚ ਰੇਡੀਅਲ ਜਾਂ ਘੁਮਾਉਦਾਰ ਸਮਤਾ ਹੁੰਦੀ ਹੈ। ਤਾਰਾ ਮੱਛੀ , ਸਮੁੰਦਰੀ ਲਿਲੀ ਵਿੱਚ ਪੰਜ'ਭੁਜੀ ਸਮਤਾ ਹੁੰਦੀ ਹੈ।

ਰਸਾਇਣ ਵਿਗਿਆਨ ਵਿੱਚ

ਸਮਾਜਿਕ ਮੇਲਜੋਲਾਂ ਵਿੱਚ

ਕਲਾ ਵਿੱਚ

ਆਰਟੀਟੈਕਚਰ ਵਿੱਚ

ਆਰਕੀਟੈਕਚਰ ਦੇ ਹਰ ਨਾਪ 'ਚ ਸਮਤਾ ਹੈ। ਇਮਾਰਤਾਂ ਦੇ ਵਿੱਚ ਸਮਤਾ ਦੇਖਣ ਨੂੰ ਮਿਲਦੀ ਹੈ ਜਿਵੇ ਤਾਜ ਮਹਿਲ ਅਮਰੀਕਾ ਦੇ ਰਾਸਟਰਪਤੀ ਦਾ ਦਫਤਰ ਵਾਈਟ ਹਾਊਸ^[3]^[4] ਇਰਾਨ ਦੇ ਸ਼ਹਿਰ ਇਸ਼ਫਾਨ ਵਿੱਚ ਮਸਜਿਦ ਦੀ ਛੱਤ ਦੀ ਸਮਤਾ ਅੱਠ ਪਾਸੀ ਹੈ

ਮਿੱਟੀ ਦੇ ਬਰਤਨਾਂ ਅਤੇ ਧਾਤ ਦੀਆਂ ਸੁਰਾਹੀਆਂ ਵਿੱਚ

ਗੱਦਿਆਂ ਵਿੱਚ

ਪਰਦਿਆਂ ਅਤੇ ਗਲੀਚਿਆਂ ਵਿੱਚ

ਸੰਗੀਤ ਵਿੱਚ

ਸੰਗੀਤਿਕ ਰੂਪ

ਪਿੱਚ ਬਣਤਰਾਂ

ਅਨੁਰੂਪਤਾ

ਹੋਰ ਕਲਾ ਅਤੇ ਸ਼ਿਲਪਾਂ ਵਿੱਚ

ਸੁਹਜ-ਸ਼ਾਸਤਰਾਂ ਵਿੱਚ

ਸਾਹਿਤ ਵਿੱਚ

ਹਵਾਲੇ

↑ For instance, Venema 2006, p. 122 and Henderson & Taimiṇa 2005, p. 123
↑ Josiah Royce, Ignas K. Skrupskelis (2005) The Basic Writings of Josiah Royce: Logic, loyalty, and community (Google eBook) Fordham Univ Press, p. 790
↑ Williams: Symmetry in Architecture. Members.tripod.com (1998-12-31). Retrieved on 2013-04-16.
↑ Aslaksen: Mathematics in Art and Architecture. Math.nus.edu.sg. Retrieved on 2013-04-16.

[1] For instance, Venema 2006, p. 122 and Henderson & Taimiṇa 2005, p. 123

[2] Josiah Royce, Ignas K. Skrupskelis (2005) The Basic Writings of Josiah Royce: Logic, loyalty, and community (Google eBook) Fordham Univ Press, p. 790

[3] Williams: Symmetry in Architecture. Members.tripod.com (1998-12-31). Retrieved on 2013-04-16.

[4] Aslaksen: Mathematics in Art and Architecture. Math.nus.edu.sg. Retrieved on 2013-04-16.

[1]

[2]

[3]

[4]

@@ ਲਾਈਨ 21: / ਲਾਈਨ 21: @@
 ===ਰੇਖਾਗਣਿਤ ਵਿੱਚ===
+'''ਸਮਰੂਪ''' ਦੋ ਵਸਤੂਆਂ ਇਕੋ ਹੀ ਸ਼ਕਲ, ਅਕਾਰ ਦੀਆਂ ਹੋਣ ਉਸ ਨੂੰ ਸਮਰੂਪ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇੱਕ ਵਸਤੂ ਨੂੰ ਦੂਜੀ ਤੋਂ ਉਸ ਦੀਆਂ ਭੁਜਾਵਾਂ ਨੂੰ ਅਨੁਪਾਤਿਕ ਵਧਾਕੇ ਜਾਂ ਘਟਾਕੇ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਜਿਵੇ ਸਾਰੇ ਚੱਕਰ ਇੱਕ ਦੂਜੇ ਨੂੰ ਸਮਰੂਪ ਹੁੰਦੇ ਹਨ। ਸਾਰੀਆਂ ਸਮਬਾਹੂ ਤ੍ਰਿਭੁਜ ਸਮਰੂਪ ਹੁੰਦੀਆਂ ਹਨ। ਪਰ [[ਆਇਤ]], [[ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ]] ਅਤੇ [[ਅੰਡਾਕਾਰ]] ਸਮਰੂਪ ਨਹੀਂ ਹੁੰਦੇ। ਜੇ ਕਿਸੇ ਤ੍ਰਿਭੁਜ ਦੇ ਦੋ ਕੋਣਾਂ ਦੀ ਮਾਤਰਾ ਦੁਜੀ ਤ੍ਰਿਭੁਜ ਦੇ ਦੋ ਕੋਣਾਂ ਦੇ ਬਰਾਬਰ ਹੋਵੇ ਤਾਂ ਤ੍ਰਿਭੁਜ ਸਮਰੂਪ ਹੁੰਦੀਆਂ ਹਨ ਇਸ ਨਿਯਮ ਨੂੰ AAA ਸਮਰੂਪ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ <math>\triangle ABC</math> ਅਤੇ <math>\triangle A'B'C'</math> ਵਿੱਚ ਉਹਨਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਸਮਾਨ ਹੁੰਦੇ ਹਨ। ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਉਹਨਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਵਰਗ ਦੇ ਅਨੁਪਾਤ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।<ref>For instance, {{harvnb|Venema|2006|loc=p. 122}} and {{harvnb|Henderson|Taimiṇa|2005|loc=p. 123}}</ref>
+====ਨਿਯਮ====
+ਜੇ <math> \angle BAC</math>
+ਅਤੇ
+<math>\angle B'A'C'</math>
+ਕੋਣਾਂ ਦਾ ਮਾਪ ਅਤੇ
+<math>\angle ABC</math>
+ਅਤੇ
+<math>\angle A'B'C'</math>
+ਦਾ ਮਾਪ ਬਰਾਬਰ ਹੋਵੇ ਤਾਂ ਤੀਜਾ ਕੋਣ
+<math>\angle ACB</math>
+ਅਤੇ
+<math>\angle A'C'B'</math>
+ਬਰਾਬਰ ਹੀ ਹੁੰਦੇ ਹਨ ਤਾਂ ਦੋਨੋ ਤ੍ਰਿਭੁਜ ਸਮਰੂਪ ਹੁੰਦੇ ਹਨ।
+:<math>\triangle ABC\sim\triangle A'B'C' \, </math>.
+ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਸਾਰੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਇਕੋ ਹੀ ਅਨੁਪਾਤ ਵਿੱਚ ਹੁੰਦੀਆਂ ਹਨ।
+: <math> {AB \over A'B'} = {BC \over B'C'} = {AC \over A'C'}</math>. ਤਾਂ ਤ੍ਰਿਭੁਜਾ ਸਮਰੂਪ ਹਨ।
+ਜੇ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਦੋ ਭੁਜਾਵਾਂ ਇਕੋ ਹੀ ਅਨੁਪਾਤ ਵਿੱਚ ਹੋਣ ਅਤੇ ਉਹਨਾਂ ਵਿਚਕਾਰਲਾ ਕੋਣ ਬਰਾਬਰ ਹੋਵੇ ਤਾਂ ਤ੍ਰਿਭੁਜ ਸਮਰੂਪ ਹੁੰਦੇ ਹਨ।
+: <math> {AB \over A'B'} = {BC \over B'C'} </math> ਅਤੇ <math>\angle ABC</math> ਅਤੇ <math>\angle A'B'C'</math> ਬਰਾਬਰ ਹਨ।
+ਜਦੋ ਦੋ ਤ੍ਰਿਭੁਜ <math>\triangle ABC</math> ਅਤੇ <math>\triangle A'B'C'</math> ਸਮਰੂਪ ਹੋਣ ਤਾਂ ਉਹਨਾਂ ਨੂੰ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ।
+:<math>\triangle ABC\sim\triangle A'B'C' \, </math>.
 ===ਤਰਕ ਵਿੱਚ===