ਤਿਕੋਣਮਿਤੀ
ਤਿਕੋਣਮਿਤੀ (ਟਰਿਗਨੋਮੈਟਰੀ) (ਗਰੀਕ ਤਰਿਗਨੋਨ = ਤਿੰਨ ਕੋਣ ਅਤੇ ਮੈਟਰੋ = ਮਾਪ) ਗਣਿਤ ਦਾ ਵਿਸ਼ਾ ਹੈ, ਜੋ ਕਿ ਕੋਣ, ਤਿਕੋਣਾਂ (ਜੁਮੈਟਰੀ ਅਤੇ ਤਿਕੋਣਮਿਤੀ ਫੰਕਸ਼ਨਾਂ ਜਿਵੇਂ ਕਿ ਸਾਈਨ, ਕੋਸਾਈਨ ਅਤੇ ਟੈਨਜੈਂਟ ਬਾਰੇ ਹੈ। ਇਸ ਦਾ ਜੁਮੈਟਰੀ ਨਾਲ ਕੁਝ ਸਬੰਧ ਹੈ, ਹਾਲਾਂਕਿ ਇਹ ਮੁੱਦੇ ਉੱਤੇ ਸਹਿਮਤੀ ਨਹੀਂ ਹੈ ਕਿ ਸਬੰਧ ਹੈ ਕਿਵੇਂ। ਕੁਝ ਲੋਕਾਂ ਲਈ ਤਿਕੋਣਮਿਤੀ ਜੁਮੈਟਰੀ ਦਾ ਹੀ ਭਾਗ ਹੈ।
ਸ਼ੁਰੂਆਤੀ ਇਤਿਹਾਸ[ਸੋਧੋ]
ਤਿਕੋਣਮਿਤੀ ਦੀਆਂ ਮੂਲ ਨਿਸ਼ਾਨੀਆਂ 3000 ਸਾਲ ਪਹਿਲਾਂ ਪ੍ਰਾਚੀਨ ਸਭਿਆਤਾਵਾਂ ਮਿਸਰ, ਬੇਬੀਲੋਨ ਅਤੇ ਸਿੰਧ ਘਾਟੀ ਦੇ ਖੰਡਰਾਂ ਵਿੱਚ ਮਿਲਦੀਆਂ ਹਨ। ਭਾਰਤੀ ਗਣਿਤ ਸਾਸਤਰੀ ਖਗੋਲੀ ਪਿੰਡਾਂ ਦੀਆਂ ਦੂਰੀਆਂ ਦੇ ਹਿਸਾਬ ਕਿਤਾਬ ਲਈ ਤਿਕੋਣਮਿਤੀ ਦੇ ਨਾਲ ਨਾਲ ਬੀਜ ਗਣਿਤ ਅਲਜਬਰਾ ਦਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਲਈ ਮੋਹਰੀਆਂ ਵਿੱਚੋਂ ਸਨ। ਅੱਜ ਲਾਗਾਧਾਇੱਕੋ ਇੱਕ ਗਿਆਤ ਗਣਿਤ ਸਾਸਤਰੀ ਹੈ ਜਿਸ ਨੇ ਆਪਣੀ ਕਿਤਾਬ ਵੇਦਾਂਗਾ ਜੋਤਿਸ਼ ਵਿੱਚ ਤਾਰਾ ਵਿਗਿਆਨ ਲਈ ਜੁਮੈਟਰੀ ਅਤੇ ਟਰਿਗਨੋਮੈਟਰੀ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤੀ। ਉਸ ਦੀਆਂ ਬਹੁਤੀਆਂ ਲਿਖਤਾਂ ਬਾਹਰੀ ਹਮਲਾਵਰਾਂ ਨੇ ਖਤਮ ਕਰ ਦਿੱਤੀਆਂ ਸਨ।
ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ[ਸੋਧੋ]
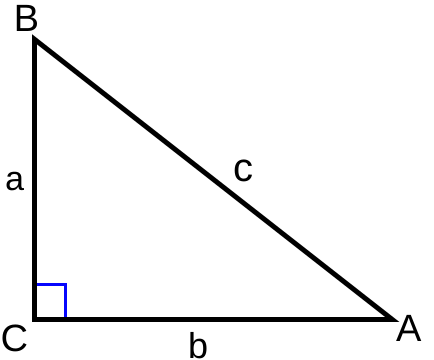
ਕੁਝ ਗਣਿਤਕਾਰ ਵਲੋਂ ਇਹ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਤਿਕੋਣਮਿਤੀ ਨੂੰ ਅਸਲ ਵਿੱਚ ਸਨਡਿਲ, ਸਭ ਤੋਂ ਪੁਰਾਣੀਆਂ ਕਿਤਾਬਾਂ ਵਿੱਚ ਪੁਰਾਤਨ ਅਧਿਆਇ, ਗਣਨਾ ਲਈ ਖੋਜਿਆ ਗਿਆ ਸੀ। ਇਹ ਸਰਵੇ ਲਈ ਵੀ ਖਾਸ ਮਹੱਤਵਪੂਰਨ ਹੈ।



