ਐਪੀਮੌਰਫਿਜ਼ਮ
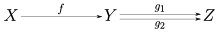
ਇੱਕ ਐਪੀਮੌਰਫਿਜ਼ਮ (ਕਦੇ ਕਦੇ ਇਸਨੂੰ ਇੱਕ ਕਵਰ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ) ਇੱਕ ਸਰਜੈਕਟਿਵ (ਫੰਕਸ਼ਨ ਦੀ ਤਸਵੀਰ ਅਤੇ ਕੋਮਡੋਮੇਨ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ) ਹੋਮੋਮੌਰਫਿਜ਼ਮ ਹੁੰਦੀ ਹੈ। ਇਸ ਦੇ ਸਮਾਨ ਹੀ f: A → B ਇੱਕ ਐਪੀਮੌਰਫਿਜ਼ਮ ਹੋਵੇਗੀ ਜੇਕਰ ਇਸ ਦਾ ਇੱਕ ਸੱਜਾ ਇਨਵਰਸ g ਹੋਵੇਗਾ: B → A, ਯਾਨਿ ਕਿ, ਜੇਕਰ ਸਾਰੇ b ∈ B ਲਈ f(g(b)) = b ਹੋਵੇ।
ਪਰਿਭਾਸ਼ਾ
[ਸੋਧੋ]ਕੈਟੇਗਰੀ ਥਿਊਰੀ ਵਿੱਚ, ਇੱਕ ਐਪੀਮੌਰਫਿਜ਼ਮ (ਜਿਸ ਨੂੰ ਇੱਕ ਐਪਿਕ ਮੌਰਫਿਜ਼ਮ ਜਾਂ ਬੋਚਾਨ ਦੀ ਭਾਸ਼ਾ ਵਿੱਚ ਇੱਕ ਐਪੀ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ) ਇੱਕ ਅਜਿਹੀ ਮੌਰਫਿਜ਼ਮ f: X → Y ਹੁੰਦੀ ਹੈ ਜੋ ਸੱਜੇ ਪਾਸੇ ਨੂੰ ਇਸ ਤਰਾਂ ਕੈਂਸੇਲਟਿਵ ਹੁੰਦੀ ਹੈ ਕਿ, ਸਾਰੀਆਂ ਮੌਰਫਿਜ਼ਮਾਂ g1, g2: Y → Z ਲਈ,
ਐਪੀਮੌਰਫਿਜ਼ਮਾਂ ਸਰਜੈਕਟਿਵ ਫੰਕਸ਼ਨਾਂ ਦੇ ਕੈਟੇਗੋਰਿਕ ਤੌਰ 'ਤੇ ਸਮਾਨ ਹੁੰਦੀਆਂ ਹਨ (ਅਤੇ ਸੈੱਟਾਂ ਦੀ ਕੈਟੇਗਰੀ ਵਿੱਚ ਇਹ ਧਾਰਨਾ ਸਰਜੈਕਟਿਵ ਫੰਕਸ਼ਨਾਂ ਨਾਲ ਸਬੰਧ ਰੱਖਦੀ ਹੈ), ਪਰ ਇਹ ਸਾਰੇ ਸੰਦਰਭਾਂ ਵਿੱਚ ਇੰਨਬਿੰਨ ਹੋਣੀ ਜਰੂਰੀ ਨਹੀਂ ; ਉਦਾਹਰਨ ਦੇ ਤੌਰ 'ਤੇ, ਨੂੰ ਸ਼ਾਮਿਲ ਕਰਨਾ ਇੱਕ ਰਿੰਗ-ਐਪੀਮੌਰਫਿਜ਼ਮ ਹੈ। ਕਿਸੇ ਐਪੀਮੌਰਫਿਜ਼ਮ ਦੀ ਡਿਊਲ ਇੱਕ ਮੋਨੋਮੌਰਫਿਜ਼ਮ ਹੁੰਦੀ ਹੈ (ਯਾਨਿ ਕੀ ਕਿਸੇ ਕੈਟੇਗਰੀ C ਵਿੱਚ ਐਪੀਮੌਰਫਿਜ਼ਮ ਡਿਊਲ ਕੈਟੇਗਰੀ ਅਂਦਰ ਇੱਕ ਮੋਨੋਮੌਰਫਿਜ਼ਮ Cop) ਹੁੰਦੀ ਹੈ)
ਅਮੂਰਤ ਅਲਜਬਰੇ ਅਤੇ ਬ੍ਰਹਿਮੰਡੀ ਅਲਜਬਰੇ ਵਿੱਚ ਕਈ ਵਿਦਵਾਨ ਕਿਸੇ ਐਪੀਮੌਰਫਿਜ਼ਮ ਨੂੰ ਸਰਲਤਾ ਨਾਲ ਇੱਕ ਔਨਟੋ ਜਾਂ ਸਰਜੈਕਟਿਵ ਹੋਮੋਮੌਰਫਿਜ਼ਮ ਪਰਿਭਾਸ਼ਿਤ ਕਰਦੇ ਹਨ। ਇਸ ਅਲਜਬਰਿਕ ਸਮਝ ਵਿੱਚ ਹਰੇਕ ਐਪੀਮੌਰਫਿਜ਼ਮ, ਕੈਟੇਗਰੀ ਥਿਊਰੀ ਦੀ ਸਮਝ ਵਿੱਚ ਇੱਕ ਐਪੀਮੌਰਫਿਜ਼ਮ ਹੁੰਦੀ ਹੈ, ਪਰ ਸਾਰੀਆਂ ਕੈਟੇਗਰੀਆਂ ਵਿੱਚ ਇਸ ਦਾ ਉਲਟ ਸੱਚ ਨਹੀਂ ਹੁੰਦਾ। ਇਸ ਆਰਟੀਕਲ ਵਿੱਚ, ਸ਼ਬਦ “ਐਪੀਮੌਰਫਿਜ਼ਮ” ਉੱਪਰ ਦਿੱਤੀ ਕੈਟੇਗਰੀ ਥਿਊਰੀ ਦੀ ਸਮਝ ਮੁਤਾਬਿਕ ਵਰਤਿਆ ਜਾਵੇਗਾ। ਇਸ ਤੇ ਹੋਰ ਜਾਣਕਾਰੀ ਲਈ, ਥੱਲੇ “ਸ਼ਬਦਾਵਲੀ” ਉੱਤੇ ਸੈਕਸ਼ਨ ਦੇਖੋ।


