ਗਾਮਾ ਫੰਕਸ਼ਨ

ਗਣਿਤ ਵਿੱਚ, ਗਾਮਾ ਫੰਕਸ਼ਨ (ਜਿਸ ਨੂੰ ਪ੍ਰਾਚੀਨ ਯੂਨਾਨੀ ਵਰਣਮਾਲਾ ਦੇ ਵੱਡੇ ਅੱਖਰ ਗਾਮਾ Γ ਦੁਆਰਾ ਦਰਸਾਇਆਜਾਂਦਾ ਹੈ), ਇਹ ਫੈਕਟੋਰੀਅਲ ਫੰਕਸ਼ਨ ਦੀ ਇੱਕ ਐਕਸਟੈਨਸ਼ਨ ਹੈ, ਜਿਸਦਾ ਆਰਗੂਮੈਂਟ 1 ਘਟਾ ਕੇ, ਵਾਸਤਵਿਕ ਅਤੇ ਗੁੰਝਲਦਾਰ ਨੰਬਰਾਂ ਤੱਕ ਕੀਤੀ ਗਈ ਹੈ। ਜੇ n ਇੱਕ ਸਕਾਰਾਤਮਕ ਪੂਰਨ ਅੰਕ ਹੈ,
ਗਾਮਾ ਫੰਕਸ਼ਨ ਨੂੰ ਗੈਰ-ਸਾਕਾਰਾਤਮਕ ਪੂਰਨ ਅੰਕਾਂ ਨੂੰ ਛੱਡਕੇ ਸਾਰੀਆਂ ਗੁੰਝਲਦਾਰ ਸੰਖਿਆਵਾਂ ਲਈ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਗਿਆ ਹੈ। ਸਕਾਰਾਤਮਕ ਵਾਸਤਵਿਕ ਹਿੱਸੇ ਵਾਲੀਆਂ ਗੁੰਝਲਦਾਰ ਸੰਖਿਆਵਾਂ ਲਈ, ਇਸ ਨੂੰ ਇੱਕ ਨਿਰੰਤਰ ਅਢੁਕਵੇਂ ਇੰਟੀਗਰਲ ਰਾਹੀਂ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ:
ਇਸ ਇੰਟੀਗਰਲ ਫੰਕਸ਼ਨ ਨੂੰ ਵਿਸ਼ਲੇਸ਼ਣੀ ਨਿਰੰਤਰਤਾ ਦੁਆਰਾ ਗੈਰ-ਸਾਕਾਰਾਤਮਕ ਪੂਰਨ ਅੰਕਾਂ (ਜਿੱਥੇ ਕਿ ਫੰਕਸ਼ਨ ਦੇ ਸਰਲ ਧਰੁਵ ਹਨ) ਨੂੰ ਛੱਡ ਕੇ ਸਾਰੀਆਂ ਗੁੰਝਲਦਾਰ ਸੰਖਿਆਵਾਂ ਤੱਕ ਵਧਾ ਦਿੱਤਾ ਗਿਆ ਹੈ, ਜਿਸ ਤੋਂ ਮੈਰੋਮੋਰਫਿਕ ਫੰਕਸ਼ਨ ਮਿਲਦਾ ਹੈ ਜਿਸ ਨੂੰ ਅਸੀਂ ਗਾਮਾ ਫੰਕਸ਼ਨ ਨੂੰ ਕਹਿੰਦੇ ਹਾਂ। ਇਸਦੀਆਂ ਕੋਈ ਸਿਫਰਾਂ ਨਹੀਂ ਹੁੰਦੀਆਂ, ਇਸ ਲਈ ਉਲਟ ਗਾਮਾ ਫੰਕਸ਼ਨ 1/Γ(z) ਇੱਕ ਹੋਲੋਮੋੋਰਫਿਕ ਫੰਕਸ਼ਨ ਹੈ। ਵਾਸਤਵ ਵਿੱਚ ਗਾਮਾ ਫੰਕਸ਼ਨ ਨੈਗੇਟਿਵ ਘਾਤ ਫੰਕਸ਼ਨ ਦੇ ਮੇਲਿਨ ਰੂਪਾਂਤਰ ਨਾਲ ਮੇਲ ਖਾਂਦਾ ਹੈ:
ਗਾਮਾ ਫੰਕਸ਼ਨ ਵਭਿੰਨ ਸੰਭਾਵਨਾ-ਡਿਸਟ੍ਰੀਬਿਊਸ਼ਨ ਫੰਕਸ਼ਨਾਂ ਵਿੱਚ ਇੱਕ ਅੰਗ ਹੈ, ਅਤੇ ਇਸੇ ਤਰ੍ਹਾਂ ਇਹ ਸੰਭਾਵਨਾ ਅਤੇ ਅੰਕੜਾ-ਵਿਗਿਆਨ ਦੇ ਖੇਤਰਾਂ ਵਿੱਚ, ਅਤੇ ਨਾਲ ਹੀ ਤਰਕੀਬੀ-ਹਿਸਾਬ ਤੇ ਲਾਗੂ ਹੈ।
ਪ੍ਰੇਰਣਾ[ਸੋਧੋ]
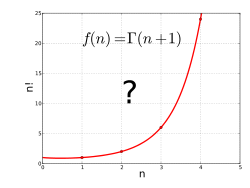
ਗਾਮਾ ਫੰਕਸ਼ਨ ਨੂੰ ਹੇਠਾਂ ਦਿੱਤੀ ਇੰਟਰਪੋਲਸ਼ਨ ਸਮੱਸਿਆ ਦਾ ਹੱਲ ਵਜੋਂ ਵੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ:
- "ਇਕ ਨਿਰਵਿਘਨ ਵਕਰ ਲੱਭੋ ਜਿਹੜੀ x ਲਈ ਸਕਾਰਾਤਮਕ ਪੂਰਨ ਅੰਕ ਮੁੱਲ ਤੇ y = (x - 1)! ਦੁਆਰਾ ਦਿੱਤੇ ਬਿੰਦੂਆਂ (x, y) ਨੂੰ ਜੋੜਦੀ ਹੈ।"
ਪਹਿਲੇ ਕੁਝ ਫ਼ੈਕਟੋਰੀਅਲਾਂ ਦੀ ਨਿਸ਼ਾਨਦੇਹੀ ਸਪਸ਼ਟ ਕਰ ਦਿੰਦੀ ਹੈ ਕਿ ਅਜਿਹੀ ਵਕਰ ਖਿੱਚੀ ਜਾ ਸਕਦੀ ਹੈ, ਪਰ ਇਹ ਇੱਕ ਅਜਿਹਾ ਫਾਰਮੂਲਾ ਰੱਖਣਾ ਬਿਹਤਰ ਹੋਵੇਗਾ ਜੋ ਠੀਕ ਠੀਕ ਵਕਰ ਦਾ ਵਰਣਨ ਕਰੇ, ਜਿਸ ਵਿੱਚ ਆਪਰੇਸ਼ਨਾਂ ਦੀ ਗਿਣਤੀ x ਦੇ ਆਕਾਰ ਤੇ ਨਿਰਭਰ ਨਾ ਕਰਦੀ ਹੋਵੇ। ਫ਼ੈਕਟੋਰੀਅਲ, x ਲਈ ਸਧਾਰਨ ਫਾਰਮੂਲਾ x! = 1 × 2 × … × x ਦੇ ਅੰਸ਼ਕ ਮੁੱਲਾਂ ਲਈ ਸਿੱਧੇ ਤੌਰ 'ਤੇ ਨਹੀਂ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਕਿਉਂਕਿ ਇਹ ਕੇਵਲ ਉਦੋਂ ਸਹੀ ਹੈ ਜਦੋਂ x ਇੱਕ ਕੁਦਰਤੀ ਨੰਬਰ ਹੈ (ਜਿਵੇਂ ਇੱਕ ਸਕਾਰਾਤਮਕ ਪੂਰਨ ਅੰਕ)। ਸਾਪੇਖਕ ਤੌਰ 'ਤੇ ਗੱਲ ਕਰਦਿਆਂ ਫ਼ੈਕਟੋਰੀਅਲ ਲਈ ਅਜਿਹੇ ਕੋਈ ਸਧਾਰਨ ਹੱਲ ਨਹੀਂ ਹਨ; x! ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਰਕਮਾਂ, ਉਤਪਾਦਾਂ, ਸ਼ਕਤੀਆਂ, ਘਾਤਕ ਫੰਕਸ਼ਨਾਂ, ਜਾਂ ਲੌਗਰਿਦਮਾਂ ਦਾ ਕੋਈ ਸੀਮਤ ਜੋੜਮੇਲ ਕਾਫੀ ਨਹੀਂ ਹੋਵੇਗਾ!; ਪਰ ਕੈਲਕੂਲਸ ਤੋਂ ਇੰਟੈਗਰਲਾਂ ਅਤੇ ਲਿਮਿਟਾਂ ਵਰਗੇ ਸਾਧਨਾਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ ਫੈਕਟੋਰੀਅਲ ਲਈ ਇੱਕ ਆਮ ਫਾਰਮੂਲਾ ਲੱਭਣਾ ਸੰਭਵ ਹੈ। ਇਸਦਾ ਇੱਕ ਵਧੀਆ ਹੱਲ ਗਾਮਾ ਫੰਕਸ਼ਨ ਹੈ।
ਫੈਕਟੋਰੀਅਲ ਦੇ ਗੈਰ-ਇੰਟੈਗਰਲਾਂ ਤੱਕ ਅਨੰਤ ਸਾਰੇ ਨਿਰੰਤਰ ਐਕਸਟੈਨਸ਼ਨ ਹਨ: ਅਨੰਤ ਵਕਰਾਂ ਨੂੰ ਅਲੱਗ ਥਲੱਗ ਬਿੰਦੂਆਂ ਦੇ ਕਿਸੇ ਵੀ ਸਮੂਹ ਰਾਹੀਂ ਖਿੱਚਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਗਾਮਾ ਫੰਕਸ਼ਨ ਅਭਿਆਸ ਵਿੱਚ ਸਭ ਤੋਂ ਲਾਭਦਾਇਕ ਹੱਲ ਹੈ, ਕਿਉਂ ਜੋ ਇਹ ਵਿਸ਼ਲੇਸ਼ਣੀ (ਗੈਰ-ਸਕਾਰਾਤਮਕ ਪੂਰਨ ਅੰਕਾਂ ਨੂੰ ਛੱਡ ਕੇ) ਹੈ, ਅਤੇ ਇਸ ਨੂੰ ਕਈ ਤਰੀਕਿਆਂ ਨਾਲ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਹਾਲਾਂਕਿ, ਇਹ ਇਕਮਾਤਰ ਵਿਸ਼ਲੇਸ਼ਣਾਤਮਕ ਕਾਰਜ ਨਹੀਂ ਹੈ ਜੋ ਫੈਕਟਰੀਅਲ ਨੂੰ ਵਿਸਤਾਰਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ ਇਸ ਵਿੱਚ ਕੋਈ ਵਿਸ਼ਲੇਸ਼ਣੀ ਫੰਕਸ਼ਨ ਜੋੜਨ ਤੇ ਜੋ ਕਿ ਸਕਾਰਾਤਮਕ ਪੂਰਨ ਅੰਕਾਂ ਤੇ ਸਿਫ਼ਰ ਹੈ, ਜਿਵੇਂ ਕਿ k sin mπx, ਉਸ ਗੁਣ ਵਾਲਾ ਇੱਕ ਹੋਰ ਫੰਕਸ਼ਨ ਦੇਵੇਗੀ।
ਉਪਰੋਕਤ ਇੰਟਰਪੋਲੇਸ਼ਨ ਨੂੰ ਸੰਤੁਸ਼ਟ ਕਰਨ ਨਾਲੋਂ ਵੱਧ ਇੱਕ ਹੋਰ ਅੰਦਰੂਨੀ ਗੁਣ ਫੈਕਟਰੀਅਲ ਫੰਕਸ਼ਨ ਦੇ ਅਨੁਵਾਦਿਤ ਵਰਜ਼ਨ ਨੂੰ ਪਰਿਭਾਸ਼ਤ ਕਰਦੇ ਹੋਏ ਮੁੜ-ਮੁੜ ਵਾਪਰਦੇ ਸੰਬੰਧ ਨੂੰ ਸੰਤੁਸ਼ਟ ਕਰਨਾ ਹੈ,
ਪਰਿਭਾਸ਼ਾ[ਸੋਧੋ]
ਮੁੱਖ ਪਰਿਭਾਸ਼ਾ[ਸੋਧੋ]
ਨੋਟੇਸ਼ਨ Γ(z) Legendre ਕਰਕੇ ਹੈ। ਜੇ ਕੰਪਲੈਕਸ ਨੰਬਰ z ਦਾ ਵਾਸਤਵਿਕ ਹਿੱਸਾ ਸਕਾਰਾਤਮਕ ਹੈ (Re(z) > 0), ਤਾਂ ਇੰਟੈਗਰਲ
ਪੂਰੀ ਤਰ੍ਹਾਂ ਨਿਰੰਤਰ ਹੈ, ਅਤੇ ਇਸ ਨੂੰ ਦੂਜੀ ਕਿਸਮ ਦੇ ਯੂਲਰ ਇੰਟੈਗਰਲ ਵਜੋਂ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ (ਪਹਿਲੀ ਕਿਸਮ ਦੇ ਯੂਲਰ ਇੰਟੈਗਰਲ ਬੀਟਾ ਫੰਕਸ਼ਨ ਪਰਿਭਾਸ਼ਿਤ ਕਰਦਾ ਹੈ)। ਭਾਗਾਂ ਦੁਆਰਾ ਇੰਟੈਗਰੇਸ਼ਨ ਦੀ ਵਰਤੋਂ ਕਰਨ ਤੇ, ਇਹ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ਕਿ:
- ਉਸਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਪਛਾਣਦੇ ਹੋਏ
ਦਿੱਤਾ ਗਿਆ ਕਿ and
ਸਾਰੇ ਸਕਾਰਾਤਮਕ ਪੂਰਨ ਅੰਕਾਂ n ਲਈ। ਇਸਨੂੰ ਆਗਮਨ ਰਾਹੀਂ ਪ੍ਰਮਾਣ ਦੀ ਇੱਕ ਉਦਾਹਰਨ ਵਜੋਂ ਵੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ।
ਇੱਕਰੂਪਤਾ ਵਰਤੇ ਜਾ ਸਕਦੇ ਹਨ (ਜਾਂ, ਇੱਕੋ ਹੀ ਨਤੀਜੇ ਦੇਣ ਨਾਲ, ਵਿਸ਼ਲੇਸ਼ਣੀ ਨਿਰੰਤਰਤਾ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ) ਅਦੁੱਤੀ ਢੰਗ ਨਾਲ ਸਿਵਾਏ ਜ਼ੀਰੋ ਤੋਂ ਘੱਟ ਜਾਂ ਇਸਦੇ ਬਰਾਬਰ ਪੂਰਨ ਅੰਕ ਦੇ \ ਗਾਮਾ(z) ਦੇ ਸਾਰੇ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਲਈ ਪਰਿਭਾਸ਼ਿਤ ਸਾਰੇ ਮੈਰੋਨੋਮੋਰਫਿਕ ਫੰਕਸ਼ਨਾਂ ਨੂੰ ਇੰਟੈਗਰਲ ਫਾਰਮੂਲੇਸ਼ਨ ਤੱਕ ਵਿਸਤਾਰਿਆ ਜਾ ਸਕਦਾ।
ਇਹ ਇਹੀ ਵਿਸਤਾਰਿਤ ਵਰਜ਼ਨ ਹੈ ਜਿਸਨੂੰ ਆਮ ਤੌਰ 'ਤੇ ਗਾਮਾ ਫੰਕਸ਼ਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।
ਹਵਾਲੇ[ਸੋਧੋ]
ਬਾਹਰੀ ਕੜੀਆਂ[ਸੋਧੋ]
- NIST Digital Library of Mathematical Functions:Gamma function
- Pascal Sebah and Xavier Gourdon. Introduction to the Gamma Function.।n PostScript and HTML formats.
- C++ reference for std::tgamma
- Examples of problems involving the gamma function can be found at Exampleproblems.com Archived 2016-10-02 at the Wayback Machine..
- Hazewinkel, Michiel, ed. (2001), "Gamma function", ਗਣਿਤ ਦਾ ਵਿਸ਼ਵਕੋਸ਼, ਸਪਰਿੰਗਰ, ISBN 978-1-55608-010-4
- Wolfram gamma function evaluator (arbitrary precision)
- Volume of n-Spheres and the Gamma Function at MathPages






![{\displaystyle {\begin{aligned}\Gamma (z+1)&=\int _{0}^{\infty }x^{z}e^{-x}\,dx\\&=\left[-x^{z}e^{-x}\right]_{0}^{\infty }+\int _{0}^{\infty }zx^{z-1}e^{-x}\,dx\\&=\lim _{x\to \infty }(-x^{z}e^{-x})-(0e^{-0})+z\int _{0}^{\infty }x^{z-1}e^{-x}\,dx\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe42711797305b2a927cf7fbdf0662359e61a1c4)


![{\displaystyle {\begin{aligned}\Gamma (1)&=\int _{0}^{\infty }x^{1-1}e^{-x}\,dx\\&=\left[-e^{-x}\right]_{0}^{\infty }\\&=\lim _{x\to \infty }(-e^{-x})-(-e^{-0})\\&=0-(-1)\\&=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/317aa768c56671b538d84ad774fa2a00e4ab6fe1)



