ਸੰਸਾਰ ਰੇਖਾ
ਫਿਜਿਕਸ ਵਿੱਚ, ਕਿਸੇ ਵਸਤੂ ਦੀ ਸੰਸਾਰ ਰੇਖਾ ਉਸ ਵਸਤੂ ਦਾ ਨਿਰਾਲਾ ਰਸਤਾ ਹੁੰਦਾ ਹੈ ਜੋ ਉਹ 4-ਅਯਾਮੀ ਸਪੇਸ ਸਮੇਂ ਰਾਹੀਂ ਲੰਘਦੇ ਵਕਤ ਤੈਅ ਕਰਦੀ ਹੈ। ਸੰਸਾਰ ਰੇਖਾ ਦਾ ਵਿਚਾਰ ‘ਚਕੱਰਪਥ’ ਜਾਂ ‘ਟਰੈਜੈਕਟਰੀ’ (ਜਿਵੇਂ ਸਪੇਸ ਵਿੱਚ ਇੱਕ ਚੱਕਰਪਥ ਜਾਂ ਕਿਸੇ ਨਕਸ਼ੇ ਤੇ ਇੱਕ ਟਰੱਕ ਦੀ ਟਰੈਜੈਕਟਰੀ) ਤੋਂ ਸਮੇਂ ਦੇ ਅਯਾਮ ਰਾਹੀਂ ਵੱਖਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਅਤੇ ਆਮ ਤੌਰ ਤੇ ਸਪੇਸ ਦਾ ਵਿਸ਼ਾਲ ਖੇਤਰਫਲ ਸ਼ਾਮਿਲ ਕਰਦਾ ਹੈ ਜਿੱਥੇ ਸਮਝ ਮੁਤਾਬਿਕ ਸਿੱਧੇ ਰਸਤੇ ਉਹਨਾਂ ਦੀ ਸਬੰਧਿਤ ਜਿਆਦਾ ਸ਼ੁੱਧ ਪੋਜੀਸ਼ਨ ਦੀ ਅਵਸਥਾ ਦਿਖਾਉਣ ਲਈ ਦੁਬਾਰਾ ਜੋੜੇ ਜਾਂਦੇ ਹਨ-ਸਪੈਸ਼ਲ ਰੀਲੇਟਿਵਿਟੀ ਜਾਂ ਗਰੈਵਿਟੇਸ਼ਨਲ ਪ੍ਰਕ੍ਰਿਆਵਾਂ ਦੇ ਸੁਭਾਅ ਨੂੰ ਵਿਅਕਤ ਕਰਨ ਲਈ। ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਦਾ ਵਿਚਾਰ ਫਿਜਿਕਸ ਵਿੱਚ ਪੈਦਾ ਹੋਇਆ ਅਤੇ ਹਰਮਨ ਮਿੰਕੋਵਸਕੀ ਦੁਆਰਾ ਅੱਗੇ ਵਧਾਇਆ ਗਿਆ। ਇਹ ਸ਼ਬਦ ਹੁਣ ਅਕਸਰ ਰੀਲੇਟੀਵਿਟੀ ਥਿਊਰੀਆਂ ਵਿੱਚ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ {ਯਾਨਿ ਕਿ ਸਪੈਸ਼ਲ ਤੇ ਜਨਰਲ ਰੀਲੇਟਿਵਿਟੀ ਵਿੱਚ}।
ਫੇਰ ਵੀ, ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਘਟਨਾਵਾਂ ਦੀ ਕਾਰਜਪ੍ਰਣਾਲੀ ਪੇਸ਼ ਕਰਨ ਦਾ ਇੱਕ ਆਮ ਤਰੀਕਾ ਹੈ। ਇਸਦੀ ਵਰਤੋ ਕਿਸੇ ਖਾਸ ਥਿਊਰੀ ਨਾਲ ਨਹੀਂ ਬੰਨੀ ਹੋਈ ਹੈ। ਇਸਲਈ ਆਮ ਵਰਤੋ ਵਿੱਚ, ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਨਿੱਜੀ ਇਨਸਾਨੀ ਘਟਨਾਵਾਂ (ਸਮੇਂ ਅਤੇ ਸਥਾਨ ਨਾਲ ਅਯਾਮਾਂ ਦੇ ਤੌਰ ਤੇ) ਦਾ ਲੜੀਵਾਰ ਰਸਤਾ ਹੈ ਜੋ ਇੱਕ ਇਨਸਾਨ ਦਾ ਇਤਿਹਾਸ ਦਰਸਾਉਂਦਾ ਹੈ- ਸ਼ਾਇਦ ਕਿਸੇ ਦੇ ਜਨਮ ਦੇ ਸਮੇਂ ਅਤੇ ਸਥਾਨ ਤੋਂ ਸ਼ੁਰੂ ਕਰਕੇ ਤੋਂ ਮੌਤ ਤੱਕ ਦੇ ਸਮੇਂ ਅਤੇ ਸਥਾਨ ਤੱਕ ਦਾ ਰਸਤਾ। ਇੱਕ ਜਹਾਜ ਦੀ ਲੌਗ-ਪੁਸਤਕ ਜਹਾਜ ਦੀ ਸੰਸਾਰ ਰੇਖਾ ਦਾ ਵਿਸਤਾਰ ਹੈ, ਜਿੰਨੀ ਦੇਰ ਇਹ ਹਰੇਕ ਪੁਜੀਸ਼ਨ ਨਾਲ ਜੁੜੇ ਸਮੇਂ ਦਾ ਬੰਧਨ ਰੱਖਦਾ ਹੈ। ਸੰਸਾਰ ਰੇਖਾ ਕਿਸੇ ਨੂੰ ਧਰਤੀ ਦੀ ਗੋਲ ਸਤਹਿ ਲਈ ਸਹੀ ਦਿੱਤੇ ਹੋਏ ਦੂਰੀ ਦੇ ਨਾਪ(ਮੀਟ੍ਰਿਕ) ਤੇ ਜਹਾਜ ਦੀ ਸਪੀਡ ਦਾ ਹਿਸਾਬ ਲਗਾਉਣ ਦਿੰਦੀ ਹੈ।
ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ ਵਰਤੋਂ
[ਸੋਧੋ]ਫਿਜਿਕਸ ਵਿੱਚ, ਇੱਕ ਵਸਤੂ (ਸਪੇਸ ਵਿੱਚ ਲਗਭਗ ਇੱਕ ਬਿੰਦੂ ਦੀ ਤਰਾਂ, ਜਿਵੇਂ, ਇੱਕ ਕਣ ਜਾਂ ਦਰਸ਼ਕ) ਦੀ ਸੰਸਾਰ ਰੇਖਾ, ਵਸਤੂ ਦੇ ਇਤਿਹਾਸ ਨਾਲ ਸਬੰਧਿਤ ਸਪੇਸ ਸਮਾਂ ਘਟਨਾਵਾਂ ਦੀ ਲੜੀ ਹੁੰਦੀ ਹੈ। ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਤਰਾਂ ਦੀ ਵਕਰ (curve) ਹੁੰਦੀ ਹੈ। ਹੇਠਾਂ ਇੱਕ ਬਰਾਬਰ ਪਰਿਭਾਸ਼ਾ ਸਮਝਾਈ ਜਾਵੇਗੀ: ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਸਮੇਂ ਵਰਗੀ ਵਕਰ ਹੁੰਦੀ ਹੈ। ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਉੱਤੇ ਹਰੇਕ ਬਿੰਦੂ ਇੱਕ ਘਟਨਾ ਹੈ ਜੋ ਉਸ ਵਕਤ ਤੇ ਵਸਤੂ ਦੀ ਸਥਾਨਿਕ ਪੋਜੀਸ਼ਨ ਅਤੇ ਸਮੇਂ ਨਾਲ ਲੇਬਲ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ।
ਉਦਾਹਰਨ ਵਜੋਂ, ਸਪੇਸ ਵਿੱਚ ਧਰਤੀ ਦਾ ਔਰਬਿਟ ਲਗਭਗ ਇੱਕ ਚੱਕਰ ਹੈ, ਸਪੇਸ ਵਿੱਚ ਇੱਕ 3-ਅਯਾਮੀ (ਬੰਦ) ਵਕਰ: ਧਰਤੀ ਹਰੇਕ ਸਾਲ ਸਪੇਸ ਵਿੱਚ ਉਸੇ ਬਿੰਦੂ ਤੇ ਵਾਪਸ ਆ ਜਾਂਦੀ ਹੈ। ਫੇਰ ਵੀ, ਇਹ ਉੱਥੇ ਇੱਕ ਵੱਖਰੇ (ਬਾਦ ਵਿੱਚ) ਵਕਤ ਤੇ ਪਹੁੰਚਦੀ ਹੈ। ਧਰਤੀ ਦੀ ਸੰਸਾਰ ਰੇਖਾ ਸਪੇਸ ਸਮੇਂ (ਇੱਕ 4-ਅਯਾਮੀ ਸਪੇਸ ਵਿੱਚ ਇੱਕ ਵਕਰ) ਵਿੱਚ ਕੁੰਡਲੀਦਾਰ (helical) ਹੁੰਦੀ ਹੈ ਅਤੇ ਉਸੇ ਬਿੰਦੂ ਤੇ ਨਹੀਂ ਵਾਪਸ ਆਉਂਦੀ।
ਸਪੇਸ ਸਮਾਂ ਬਿੰਦੂਆਂ ਦਾ ਸੰਗ੍ਰਿਹ ਹੈ ਜਿਨਾਂ ਨੂੰ ਘਟਨਾਵਾਂ ਕਹਿੰਦੇ ਹਨ, ਇੱਕ ਨਿਰੰਤਰ ਅਤੇ ਪੱਧਰੇ ਨਿਰਦੇਸ਼-ਅੰਕ ਸਿਸਟਮ ਨਾਲ ਜੋ ਘਟਨਾਵਾਂ ਨੂੰ ਪਛਾਣਦਾ ਹੈ। ਹਰੇਕ ਘਟਨਾ ਚਾਰ ਨੰਬਰਾਂ ਨਾਲ ਲੇਬਲ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ: ਇੱਕ ਵਕਤ ਦਾ ਨਿਰਦੇਸ਼ ਅੰਕ ਅਤੇ ਤਿੰਨ ਸਪੇਸ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ; ਇਸਲਈ ਸਪੇਸ ਸਮਾਂ ਇੱਕ 4-ਅਯਾਮੀ ਸਪੇਸ ਹੈ। ਸਪੇਸ ਸਮੇਂ ਲਈ ਗਣਿਤਿਕ ਸ਼ਬਦ ਇੱਕ 4-ਅਯਾਮੀ ਬਹੁ-ਪਰਤ (manifold) ਹੈ। ਇਹ ਧਾਰਨਾ ਉੱਚ-ਅਯਾਮੀ ਸਪੇਸ ਤੇ ਵੀ ਚੰਗੀ ਤਰਾਂ ਲਾਗੂ ਹੁੰਦੀ ਹੈ। 4-ਅਯਾਮਾਂ ਦੀ ਸਰਲ ਤਸਵੀਰ ਲਈ, ਦੋ ਸਪੇਸ ਨਿਰਦੇਸ਼ ਦਬਾ ਦਿੱਤੇ ਜਾਂਦੇ ਹਨ। ਫੇਰ ਘਟਨਾ ਇੱਕ ਮਿੰਕੋਵਸਕੀ ਚਿੱਤਰ ਵਿੱਚ ਇੱਕ ਬਿੰਦੂ ਦੁਆਰਾ ਦਰਸਾਈ ਜਾਂਦੀ ਹੈ, ਜੋ ਵਕਤ ਦੇ ਨਿਰਦੇਸ਼-ਅੰਕ (t) ਨਾਲ ਪਲੌਟ ਕੀਤਾ ਹੋਇਆ ਇੱਕ ਖੇਤਰਫਲ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਵਿੱਚ ਸਮਾਂ ਉੱਪਰ ਵੱਲ ਨੂੰ ਅਤੇ ਸਪੇਸ (x) ਲੇਟਵੇਂ ਤਲ (horizontally) ਹੁੰਦਾ ਹੈ। ਜਿਵੇਂ F.R. Harvey ਨੇ ਦਰਸਾਇਆ:: ਇੱਕ ਵਕਰ M ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਬਿੰਦੂ ਦੀ ਸੰਸਾਰ ਰੇਖਾ ਕਹੀ ਜਾਏਗੀ ਜੇਕਰ ਇਸਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹਰੇਕ ਬਿੰਦੂ ਤੇ ਭਵਿੱਖ ਸਮੇਂ ਵਰਗੀ ਹੋਵੇ। ਵਕਰ-ਲੰਬਾਈ ਦਾ ਪੈਰਾਮੀਟਰ ਉਚਿਤ ਸਮਾਂ (ਇੱਕੋ ਸਮੇਂ ਦੋ ਘਟਨਾਵਾਂ ਦਾ ਗੁਜ਼ਰਿਆ ਸਮਾਂ) ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਤੇ τ ਨਾਲ ਲਿਖਿਆ ਜਾਂਦਾ ਹੈ। M ਦੀ ਲੰਬਾਈ ਸੰਸਾਰ ਰੇਖਾ ਜਾਂ ਕਣ ਦਾ ਉਚਿਤ ਸਮਾਂ ਕਹੀ ਜਾਂਦੀ ਹੈ। ਜੇਕਰ ਸੰਸਾਰ ਰੇਖਾ M ਇੱਕ ਰੇਖਾ ਦਾ ਹਿੱਸਾ ਹੈ, ਤਾਂ ਕਣ ਨੂੰ ਮੁਕਤ ਗਿਰਾਵਟ (free fall) ਵਿੱਚ ਹੁੰਦਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। (ਮੁਕਤ ਗਿਰਾਵਟ ਉਹ ਅਵਸਥਾ ਹੈ ਜਦੋਂ ਸਿਰਫ ਕਿਸੇ ਵਸਤੂ ਦਾ ਵਜ਼ਨ ਹੀ ਉਸਤੇ ਲੱਗ ਰਿਹਾ ਇੱਕਮਾਤਰ ਬਲ ਹੋਵੇ)
ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਸਿੰਗਲ ਬਿੰਦੂ ਦਾ ਰਸਤਾ ਟਰੇਸ ਕਰਦੀ ਹੈ। ਇੱਕ ਸੰਸਾਰ-ਸ਼ੀਟ 2-ਅਯਾਮੀ ਸਤਹਿ ਸਮਾਨ ਹੁੰਦੀ ਹੈ ਜੋ ਇੱਕ 1-ਅਯਾਮੀ ਰੇਖਾ (ਸਟਰਿੰਗ ਵਾਂਗ) ਦੁਆਰਾ ਸਪੇਸ ਸਮੇਂ ਰਾਹੀਂ ਲੰਘਦੇ ਵਕਤ ਬਣਾਈ (ਟਰੇਸ ਕੀਤੀ) ਜਾਂਦੀ ਹੈ। ਇੱਕ ਖੁੱਲੇ ਸਟਰਿੰਗ (ਖੁੱਲੇ ਸਿਰਿਆਂ ਨਾਲ) ਦੀ ਸੰਸਾਰ-ਸ਼ੀਟ ਇੱਕ ਪੱਟੀ ਹੁੰਦੀ ਹੈ; ਤੇ ਇੱਕ ਬੰਦ ਸਟਰਿੰਗ (ਇੱਕ ਲੂਪ) ਦੀ ਸੰਸਾਰ-ਸ਼ੀਟ ਇੱਕ ਘਣਫਲ (volume) ਹੁੰਦਾ ਹੈ।
ਇੱਕ ਵਾਰ ਵਸਤੂ ਜੇਕਰ ਸਿਰਫ ਇੱਕ ਬਿੰਦੂ ਦੇ ਤੌਰ ਤੇ ਨਹੀਂ ਅਨੁਮਾਨਿਤ ਕੀਤੀ ਜਾਂਦੀ ਸਗੋਂ ਵਧਿਆ ਹੋਇਆ ਘਣਫਲ ਰੱਖਦੀ ਹੋਵੇ, ਫੇਰ ਇਹ ਸੰਸਾਰ ਰੇਖਾ ਦੀ ਜਗਹ ਸੰਸਾਰ-ਟਿਊਬ ਟਰੇਸ ਕਰੇਗੀ।
ਸੰਸਾਰ ਰੇਖਾ ਘਟਨਾਵਾਂ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਇੱਕ ਔਜ਼ਾਰ ਦੇ ਰੂਪ ਵਿੱਚ
[ਸੋਧੋ]
ਸੰਸਾਰ ਰੇਖਾ, ਸੰਸਾਰ-ਸ਼ੀਟ, ਅਤੇ ਸੰਸਾਰ ਘਣਫਲ, ਕਿਉਂਕਿ ਉਹ ਕਣਾਂ, ਸਟਰਿੰਗਾਂ ਅਤੇ ਬਰੇਨਜ਼ ਦੁਆਰਾ ਬਣਦੇ ਹਨ|
ਇੱਕ 1-ਅਯਾਮੀ ਰੇਖਾ ਜਾਂ ਵਕਰ ਇੱਕ ਪੈਰਾਮੀਟਰ ਦੇ ਇੱਕ ਫੰਕਸ਼ਨ ਦੇ ਮੁੱਲ ਰਾਹੀਂ ਦਰਸਾਈ ਜਾ ਸਕਦੀ ਹੈ ਜੋ ਸਪੇਸ-ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਬਿੰਦੂ ਨਾਲ ਸਬੰਧਿਤ ਹੁੰਦੀ ਹੈ ਅਤੇ ਪੈਰਾਮੀਟਰ ਦੇ ਬਦਲਾਓ ਕਾਰਨ ਇੱਕ ਰੇਖਾ ਟਰੇਸ ਕਰਦੀ ਹੈ| ਇਸਲਈ ਗਣਿਤਿਕ ਸ਼ਬਦਾਂ ਵਿੱਚ ਇੱਕ ਵਕਰ ਚਾਰ ਨਿਰਦੇਸ਼ ਅੰਕਾਂ ਦੇ ਫੰਕਸ਼ਨ ਰਾਹੀਂ ਦਰਸਾਈ ਜਾ ਸਕਦੀ ਹੈ(ਜਿੱਥੇ ਆਮਤੌਰ ਤੇ ਸਮੇਂ ਦਾ ਨਿਰਦੇਸ਼ ਅੰਕ ਹੈ) ਜੋ ਇੱਕ ਪੈਰਾਮੀਟਰ τ ਤੇ ਨਿਰਭਰ ਹਨ| ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਨਿਰਦੇਸ਼-ਅੰਕ ਜਾਲ (grid) ਵਕਰਾਂ ਦਾ ਉਹ ਸੰਗ੍ਰਹਿ ਹੁੰਦਾ ਹੈ ਜਦੋਂ ਚਾਰ ਵਿੱਚੋਂ ਤਿੰਨ ਨਿਰਦੇਸ਼-ਅੰਕ ਫੰਕਸ਼ਨ ਸਥਿਰ ਰੱਖੇ ਜਾਣ|
ਕਦੇ ਕਦੇ, ‘ਸੰਸਾਰ-ਰੇਖਾ’ ਸ਼ਬਦ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਕਿਸੇ ਵੀ ਵਕਰ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ| ਅਜਿਹੀ ਸ਼ਬਦਾਵਲੀ ਗਲਤਵਹਿਮੀ ਪੈਦਾ ਕਰਦੀ ਹੈ| ਹੋਰ ਸਹੀ ਤੌਰ ਤੇ, ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਅਜਿਹੀ ਵਕਰ ਹੁੰਦੀ ਹੈ ਜੋ ਕਿਸੇ ਕਣ, ਦਰਸ਼ਕ ਜਾਂ ਛੋਟੀ ਵਸਤੂ ਦੇ ਇਤਿਹਾਸ ਨੂੰ ਟਰੇਸ ਕਰਦੀ ਹੈ| ਆਮਤੌਰ ਤੇ ਇੱਕ ਵਸਤੂ ਜਾਂ ਇੱਕ ਦਰਸ਼ਕ ਦੇ ਉਚਿਤ ਸਮੇਂ ਨੂੰ ਵਕਰ ਪੈਰਾਮੀਟਰ τ ਦੇ ਤੌਰ ਤੇ ਸੰਸਾਰ ਰੇਖਾ ਦੇ ਨਾਲ ਨਾਲ ਲਿਆ ਜਾਂਦਾ ਹੈ|
ਸਪੇਸ ਸਮਾਂ ਵਕਰਾਂ ਦੀਆਂ ਕੁੱਝ ਉਦਾਹਰਨਾਂ
[ਸੋਧੋ]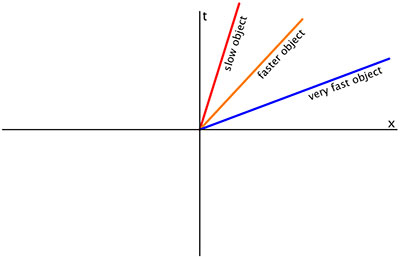
ਤਿੰਨ ਵੱਖਰੀਆਂ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਵੱਖਰੀਆਂ ਸਥਿਰ ਸਪੀਡਾਂ ਨਾਲ ਯਾਤਰਾ ਪ੍ਰਸਤੁਤ ਕਰਦੀਆਂ ਹੋਈਆਂ| t ਸਮਾਂ ਹੈ ਤੇ x ਦੂਰੀ ਹੈ|
ਇੱਕ ਵਕਰ ਜੋ ਇੱਕ ਲੇਟਵੀਂ ਰੇਖਾ ਦਾ ਭਾਗ (ਸਥਿਰ ਨਿਰਦੇਸ਼ ਅੰਕ ਵਕਤ ਤੇ ਇੱਕ ਰੇਖਾ) ਹੈ, ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਰੌਡ (a rod) ਪ੍ਰਸਤੁਤ ਕਰ ਸਕਦੀ ਹੈ ਅਤੇ ਸਹੀ ਅਰਥਾਂ ਵਿੱਚ ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਨਹੀਂ ਹੋਵੇਗੀ| ਪੈਰਾਮੀਟਰ ਰੌਡ ਦੀ ਲੰਬਾਈ ਟਰੇਸ ਕਰਦਾ ਹੈ|
ਸਥਿਰ ਸਪੇਸ ਨਿਰਦੇਸ਼ ਅੰਕ (ਉੱਪਰ ਦਰਸਾਏ ਮੁਤਾਬਿਕ ਇੱਕ ਖੜਵੀਂ ਰੇਖਾ) ਉੱਤੇ ਇੱਕ ਰੇਖਾ ਅਰਾਮ ਕਰ ਰਿਹਾ ਇੱਕ ਬਿੰਦੂ (ਜਾਂ ਇੱਕ ਗਤੀਹੀਣ ਦਰਸ਼ਕ) ਪ੍ਰਸਤੁਤ ਕਰ ਸਕਦੀ ਹੈ| ਇੱਕ ਝੁਕੀ ਹੋਈ ਰੇਖਾ ਇੱਕ ਸਥਿਰ ਨਿਰਦੇਸ਼ ਅੰਕ ਸਪੀਡ (ਸਪੇਸ ਨਿਰਦੇਸ਼ ਅੰਕ ਵਿੱਚ ਵਧ ਰਹੇ ਸਮੇਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਨਾਲ ਸਥਿਰ ਤਬਦੀਲੀ) ਨਾਲ ਇੱਕ ਬਿੰਦੂ ਪ੍ਰਸਤੁਤ ਕਰ ਸਕਦੀ ਹੈ| ਜਿੰਨੀ ਜਿਆਦਾ ਰੇਖਾ ਖੜਵੀਂ ਰੇਖਾ ਨਾਲੋਂ ਝੁਕੀ ਹੋਵੇਗੀ, ਉੰਨੀ ਹੀ ਜਿਆਦਾ ਸਪੀਡ ਤੇ ਹੋਵੇਗੀ|
ਦੋ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਜੋ ਅਲੱਗ ਅਲੱਗ ਸ਼ੁਰੂ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਫੇਰ ਇੱਕ ਦੂਜੀ ਨੂੰ ਕੱਟਦੀਆਂ ਹਨ, ਇੱਕ ਟਕਰਾਓ ਜਾਂ ‘ਮੁਕਾਬਲਾ’ ਦਰਸਾਉਂਦੀਆਂ ਹਨ| ਦੋ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਇੱਕੋ ਘਟਨਾ ਤੇ ਸ਼ੁਰੂ ਹੁੰਦੀਆਂ, ਬਾਦ ਵਿੱਚ ਅਪਣਾ ਰਸਤਾ ਅਪਣਾਉਂਦੀਆਂ, ਇੱਕ ਕਣ ਦਾ ਦੋ ਹੋਰ ਕਣਾਂ ਵਿੱਚ ਟੁੱਟ ਜਾਣਾ ਦਰਸਾ ਸਕਦੀਆਂ ਹਨ ਜਾਂ ਇੱਕ ਕਣ ਦਾ ਦੂਜੇ ਕਣ ਵਿੱਚੋਂ ਪੈਦਾ ਹੋਣਾ ਦਰਸਾ ਸਕਦੀਆਂ ਹਨ|
ਇੱਕ ਕਣ ਅਤੇ ਇੱਕ ਦਰਸ਼ਕ ਦੀਆਂ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਇੱਕ ਫੋਟੋਨ (ਪ੍ਰਕਾਸ਼ ਦਾ ਰਸਤਾ) ਦੀ ਸੰਸਾਰ ਰੇਖਾ ਨਾਲ ਅੰਦਰੂਨੀ ਤੌਰ ਤੇ ਜੋੜੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ ਅਤੇ ਇੱਕ ਚਿੱਤਰ ਬਣਾ ਸਕਦੀਆਂ ਹਨ ਜੋ ਇੱਕ ਕਣ ਰਾਹੀਂ ਇੱਕ ਫੋਟੋਨ ਦਾ ਪੈਦਾ ਹੋਣਾ ਦਰਸਾਉਂਦਾ ਹੈ ਜੋ ਬਾਦ ਵਿੱਚ ਦਰਸ਼ਕ ਦੁਆਰਾ ਦੇਖਿਆ ਜਾਂਦਾ ਹੈ (ਜਾਂ ਦੂਜੇ ਕਣ ਰਾਹੀਂ ਸੋਖ ਲਿਆ ਜਾਂਦਾ ਹੈ)
ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਦੇ ਸਦਿਸ਼ ਸਪਰਸ਼ਰੇਖਾ, ਚਾਰ-ਵਿਲੌਸਿਟੀ
[ਸੋਧੋ]ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਨੂੰ ਦਰਸਾਉਂਦੇ ਚਾਰ ਨਿਰਦੇਸ਼ ਅੰਕ ਫੰਕਸ਼ਨ, ਇੱਕ ਵਾਸਤਵਿਕ ਪਰਿਵਰਤਨਸ਼ੀਲ τ ਦੇ ਵਾਸਤਵਿਕ ਫੰਕਸ਼ਨ ਹਨ ਅਤੇ ਆਮ ਕੈਲਕੁਲਸ ਵਿੱਚ ਅਸਾਨੀ ਨਾਲ ਵਿਭੇਦਿਤ (differentiated) ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ| ਮੀਟ੍ਰਿਕ (ਇਹ ਅਨੁਭਵ ਰੱਖਣਾ ਮਹੱਤਵਪੂਰਨ ਹੈ) ਦੀ ਹੋਂਦ ਬਗੈਰ ਪੈਰਾਮੀਟਰ ਮੁੱਲ ਤੇ ਵਕਰ ਉੱਤੇ ਬਿੰਦੂ p ਅਤੇ ਜਰਾ ਹੋਰ ਅੱਗੇ ਉੱਤੇ ਇੱਕ ਬਿੰਦੂ ਦਰਮਿਆਨ ਵਿਚਕਾਰ ਅੰਤਰ ਬਾਰੇ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ| ਹੱਦ ਵਿੱਚ, ਇਸ ਅੰਤਰ ਨੂੰ ਰਾਹੀਂ ਭਾਗ ਦੇਣ ਨਾਲ ਇੱਕ ਵੈਕਟਰ (ਸਦਿਸ਼) ਪਰਿਭਾਸ਼ਿਤ ਹੁੰਦਾ ਹੈ, ਜੋ ਬਿੰਦੂ p ਤੇ ਸੰਸਾਰ ਰੇਖਾ ਦੇ ਸਦਿਸ਼ ਸਪਰਸ਼ ਰੇਖਾ ਹੁੰਦੀ ਹੈ| ਇਹ 4-ਅਯਾਮੀ ਵੈਕਟਰ ਹੁੰਦਾ ਹੈ ਜੋ ਬਿੰਦੂ p ਤੇ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ| ਇਹ ਵਸਤੂ ਦਾ ਸਧਾਰਨ 3-ਅਯਾਮੀ ਵੇਗ (velocity) ਹੁੰਦਾ ਹੈ (ਪਰ ਇਹ ਇੱਕੋ ਜਿਹਾ ਨਹੀਂ ਹੁੰਦਾ) ਅਤੇ ਇਸਲਈ 4-ਵਿਲੌਸਿਟੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਜਾਂ ਹਿੱਸਿਆਂ ਵਿੱਚ ਇੰਝ ਲਿਖਿਆ ਜਾਂਦਾ ਹੈ:
ਜਿੱਥੇ ਡੈਰੀਵੇਟਿਵ (derivatives) ਬਿੰਦੂ p ਤੇ ਲਏ ਜਾਂਦੇ ਹਨ, ਇਸਲਈ
ਬਿੰਦੂ p ਰਾਹੀਂ ਸਾਰੀਆਂ ਵਕਰਾਂ ਦਾ ਇੱਕ ਸਪਰਸ਼ ਵੈਕਟਰ ਹੁੰਦਾ ਹੈ, ਨਾ ਸਿਰਫ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਹੀ ਹੁੰਦੀਆਂ ਹਨ| ਦੋ ਵੈਕਟਰਾਂ ਦਾ ਜੋੜ ਫੇਰ ਕਿਸੇ ਹੋਰ ਵਕਰ ਦੀ ਸਪਰਸ਼ ਵੈਕਟਰ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਹੀ ਕਿਸੇ ਸਕੇਲਰ ਦੁਆਰਾ ਗੁਣਾ ਕਰਨ ਤੇ ਲਾਗੂ ਹੁੰਦਾ ਹੈ| ਇਸਲਈ ਬਿੰਦੂ p ਵਿੱਚ ਸਾਰੇ ਸਪਰਸ਼ ਵੈਕਟਰ ਇੱਕ ਰੇਖਿਕ ਸਪੇਸ ਫੈਲਾਉਂਦੇ ਹਨ, ਜਿਸਨੂੰ ਬਿੰਦੂ p ਤੇ ਸਪਰਸ਼ ਸਪੇਸ ਕਿਹਾ ਜਾਂਦਾ ਹੈ| ਉਦਾਹਰਨ ਵਜੋਂ,ਇੱਕ 2-ਅਯਾਮੀ ਸਪੇਸ ਨੂੰ ਲੈਂਦੇ ਹੋਏ, ਜਿਵੇਂ ਧਰਤੀ ਦੀ ਵਕਰੀ (curved) ਸਤਹਿ, ਇਸਦੀ ਸਪਰਸ਼ ਸਪੇਸ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਬਿੰਦੂ ਤੇ ਵਕਰੀ ਸਪੇਸ ਦੀ ਲਗਭਗ ਸਮਤਲ ਸਪੇਸ ਹੋਵੇਗੀ|
ਸਪੈਸ਼ਲ ਰੀਲੇਟੀਵਿਟੀ ਵਿੱਚ ਸੰਸਾਰ ਰੇਖਾਵਾਂ
[ਸੋਧੋ]ਹੁਣ ਤੱਕ ਘਟਨਾਵਾਂ ਦਰਮਿਆਨ ਅੰਤਰਾਲਾਂ ਨੂੰ ਦਰਸਾਉਣ ਤੋਂ ਬਗੈਰ ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ (ਅਤੇ ਸਪਰਸ਼ ਵੈਕਟਰ ਦਾ ਵਿਚਾਰ) ਦੱਸਿਆ ਗਿਆ ਹੈ| ਮੁਢਲਾ ਗਣਿਤ ਇਸ ਤਰ੍ਹਾਂ ਹੈ: ਸਪੈਸ਼ਲ ਰੀਲੇਟੀਵਿਟੀ ਦੀ ਥਿਊਰੀ ਸੰਭਵ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਉੱਤੇ ਕੁੱਝ ਦਬਾਓ ਪਾਉਂਦੀ ਹੈ| ਸਪੈਸ਼ਲ ਰੀਲੇਟੀਵਿਟੀ ਵਿੱਚ ਸਪੇਸ ਸਮੇਂ ਦਾ ਵਿਵਰਣ ਸਪੈਸ਼ਲ ਨਿਰਦੇਸ਼ ਅੰਕ ਸਿਸਟਮਾਂ ਤੱਕ ਸੀਮਤ ਹੈ ਜੋ ਪ੍ਰਵੇਗਿਤ (accelerate) ਨਹੀਂ ਹੁੰਦੇ (ਅਤੇ, ਇਸੇਤਰਾਂ ਘੁੰਮਦੇ ਵੀ ਨਹੀਂ) ਜਿਨਾਂ ਨੂੰ ਇਨਰਸ਼ੀਅਲ ਨਿਰਦੇਸ਼ ਅੰਕ ਸਿਸਟਮ (inertial coordinate systems) ਕਿਹਾ ਜਾਂਦਾ ਹੈ| ਅਜਿਹੇ ਨਿਰਦੇਸ਼-ਅੰਕ ਸਿਸਟਮਾਂ ਵਿੱਚ, ਪ੍ਰਕਾਸ਼ ਦੀ ਗਤੀ ਸਥਿਰ ਹੁੰਦੀ ਹੈ| ਸਪੇਸ ਸਮੇਂ ਦੀ ਬਣਤਰ ਇੱਕ ਬਿਲਨੀਅਰ ਫੌਮ η (bilinear form) ਨਾਲ ਨਿਰਧਾਰਤ ਹੁੰਦੀ ਹੈਜੋ ਕਿ ਘਟਨਾਵਾਂ ਦੇ ਹਰੇਕ ਜੋੜੇ ਲਈ ਇੱਕ ਵਾਸਤਵਿਕ ਨੰਬਰ ਦਿੰਦਾ ਹੈ| ਬਿਲਨੀਅਰ ਫੌਮ ਨੂੰ ਕਦੇ ਕਦੇ ਸਪੇਸ ਸਮਾਂ ਮੀਟ੍ਰਿਕ ਵੀ ਕਹਿੰਦੇ ਹਨ, ਪਰ ਕਿਉਂਕਿ ਵੱਖਰੀਆਂ ਘਟਨਾਵਾਂ ਜਦੇ ਕਦੇ 0 ਮੁੱਲ ਦਿੰਦੀਆਂ ਹਨ, ਗਣਿਤ ਦੀਆਂ ਮੀਟ੍ਰਿਕ ਸਪੇਸਾਂ ਵਿਚਲੇ ਮੀਟ੍ਰਿਕ ਤੋਂ ਉਲਟ, ਬਿਲੀਨੀਅਰ ਫੌਮ ਇੱਕ ਸਪੇਸ ਸਮੇਂ ਉੱਤੇ ਇੱਕ ਗਣਿਤਿਕ ਮੀਟ੍ਰਿਕ ਨਹੀਂ ਹੈ|
ਸਥਿਰ ਸਪੀਡ ਤੇ ਗਤੀਸ਼ੀਲ ਕਣ/ਵਸਤੂਆਂ ਦੀਆਂ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਨੂੰ ਜੀਓਡੈਸਿਕਸ (geodesics) ਕਿਹਾ ਜਾਂਦਾ ਹੈ| ਸਪੈਸ਼ਲ ਰੀਲੇਟੀਵਿਟੀ ਵਿੱਚ ਇਹ ਮਿੰਕੋਵਸਕੀ ਸਪੇਸ ਵਿੱਚ ਸਿੱਧੀਆਂ ਰੇਖਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ|
ਅਕਸਰ ਸਮਾਂ-ਯੂਨਿਟਾਂ ਅਜਿਹੀਆਂ ਚੁਣੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ਕਿ ਪ੍ਰਕਾਸ਼ ਦੀ ਗਤੀ ਇੱਕ ਫਿਕਸ ਕੋਣ ਤੇ ਰੇਖਾਵਾਂ ਦੁਆਰਾ ਪ੍ਰਸਤੁਤ ਕੀਤੀ ਜਾਂਦੀ ਹੈ, ਅਮਤੌਰ ਤੇ ਖੜਵੇਂ ਵਕਤ ਦੇ ਧੁਰੇ ਨਾਲ 45 ਡਿਗਰੀ ਤੇ ਦਿਖਾਈ ਜਾਂਦੀ ਹੈ| ਆਮ ਤੌਰ ਤੇ, ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਵਕਰਾਂ ਤਿੰਨ ਤਰਾਂ ਦੀਆਂ ਹੋ ਸਕਦੀਆਂ ਹਨ:
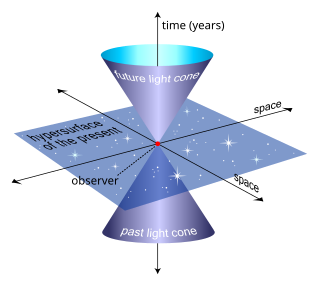
- ਪ੍ਰਕਾਸ਼-ਵਰਗੀਆਂ ਵਕਰਾਂ, ਹਰੇਕ ਬਿੰਦੂ ਤੇ ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਰੱਖਦੀਆਂ ਹੋਈਆਂ। ਇਹ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਕੋਨ ਬਣਾਉਂਦੀਆਂ ਹਨ ਤੇ ਇਸ ਨੂੰ ਦੋ ਹਿੱਸਿਆਂ ਵਿੱਚ ਵੰਢਦੀਆਂ ਹਨ। ਕੋਨ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ 3-ਅਯਾਮੀ ਹੁੰਦੀ ਹੈ, ਚਿੱਤਰ ਵਿੱਚ ਇੱਕ ਰੇਖਾ ਲਗਦੀ ਹੈ ਜਿਸਦੇ 2-ਅਯਾਮ ਦੱਬੇ ਹੋਏ ਹਨ, ਅਤੇ ਇੱਕ ਕੋਨ ਦੀ ਤਰਾਂ ਲਗਦੀ ਹੈ ਜਿਸਦਾ ਇੱਕ ਸਥਾਨਕ ਅਯਾਮ ਦਬਾਇਆ ਗਿਆ ਹੋਵੇ
- ਪ੍ਰਕਾਸ਼ ਕੋਨ ਦੀ ਇੱਕ ਉਦਾਹਰਨ, ਸਾਰੀਆਂ ਸੰਭਵ ਪ੍ਰਕਾਸ਼ ਕਿਰਨਾਂ ਦੀ 3-ਅਯਾਮੀ ਸਤਹਿ ਜੋ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਬਿੰਦੂ ਤੇ ਪਹੁੰਚਦੀਆਂ ਹਨ ਅਤੇ ਵਿੱਛੜਦੀਆਂ ਹਨ। ਇੱਥੇ, ਇੱਕ ਸਥਾਨਿਕ ਅਯਾਮ ਨੂੰ ਦਬਾ ਕੇ ਦਰਸਾਇਆ ਗਿਆ ਹੈ।
- ਸਮੇਂ-ਵਰਗੀਆਂ ਵਕਰਾਂ, ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਤੋਂ ਘੱਟ ਸਪੀਡ ਨਾਲ। ਇਹ ਵਕਰਾਂ ਪ੍ਰਕਾਸ਼ ਵਰਗੀਆਂ ਵਕਰਾਂ ਦੁਆਰਾ ਦਰਸਾਈ ਇੱਕ ਕੋਨ ਦੇ ਵਿੱਚ ਹੀ ਡਿੱਗਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ। ਸਾਡੀ ਉੱਪਰ ਦੱਸੀ ਪਰਿਭਾਸ਼ਾ ਮੁਤਾਬਿਕ: ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਸਮੇਂ-ਵਰਗੀਆਂ ਵਕਰਾਂ ਹਨ।
- ਸਪੇਸ-ਵਰਗੀਆਂ ਵਕਰਾਂ ਪ੍ਰਕਾਸ਼ ਕੋਨ ਤੋਂ ਬਾਹਰ ਡਿੱਗਦੀਆਂ ਵਕਰਾਂ। ਅਜਿਹੀਆਂ ਵਕਰਾਂ ਉਦਾਰਹਨ ਵਜੋਂ ਕਿਸੇ ਭੌਤਿਕੀ ਵਸਤੂ ਦੀ ਲੰਬਾਈ ਦਰਸਾ ਸਕਦੀਆਂ ਹਨ। ਇੱਕ ਸਲੰਡਰ ਦਾ ਘੇਰਾ ਅਤੇ ਇੱਕ ਰੌਡ ਦੀ ਲੰਬਾਈ ਸਪੇਸ-ਵਰਗੀਆਂ ਵਕਰਾਂ ਹਨ।
- ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਉੱਤੇ ਇੱਕ ਦਿੱਤੀ ਹੋਈ ਘਟਨਾ ਤੇ, ਸਪੇਸ ਸਮਾਂ (ਮਿੰਕੋਵਸਕੀ ਸਪੇਸ) ਤਿੰਨ ਹਿੱਸਿਆਂ ਵਿੱਚ ਵੰਡੀ ਜਾਂਦੀ ਹੈ:
ਕਿਸੇ ਦਿੱਤੀ ਘਟਨਾ ਦਾ ਭਵਿੱਖ ਉਹਨਾਂ ਸਾਰੀਆਂ ਘਟਨਾਵਾਂ ਰਾਹੀਂ ਬਣਦਾ ਹੈ ਜੋ ਭਵਿੱਖ ਪ੍ਰਕਾਸ਼ ਕੋਨ ਵਿਚਲੀਆਂ ਸਮੇਂ-ਵਰਗੀਆਂ ਵਕਰਾਂ ਰਾਹੀਂ ਪਹੁੰਚਦੀਆਂ ਹਨ।
ਕਿਸੇ ਦਿੱਤੀ ਘਟਨਾ ਦਾ ਭੂਤਕਾਲ ਉਹਨਾਂ ਸਾਰੀਆਂ ਘਟਨਾਵਾਂ ਨਾਲ ਬਣਦਾ ਹੈ ਜੋ ਉਸ ਘਟਨਾ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰ ਸਕਦੀਆਂ ਹਨ (ਯਾਨਿ ਕਿ, ਜੋ ਭੂਤਕਾਲ ਪ੍ਰਕਾਸ਼ ਕੋਨ ਵਿਚਲੀਆਂ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਰਾਹੀਂ ਜੁੜ ਕੇ ਦਿੱਤੀ ਘਟਨਾ ਤੱਕ ਪਹੁੰਚਦੀਆਂ ਹੋਣ)।
ਕਿਸੇ ਦਿੱਤੀ ਘਟਨਾ ਤੇ ਪ੍ਰਕਾਸ਼ ਕੋਨ ਉਹਨਾਂ ਸਾਰੀਆਂ ਘਟਨਾਵਾਂ ਰਾਹੀਂ ਬਣਦੀ ਹੈ ਜੋ ਘਟਨਾ ਦੇ ਨਾਲ ਪ੍ਰਕਾਸ਼ ਦੀਆਂ ਕਿਰਨਾਂ ਰਾਹੀਂ ਜੋੜੀਆਂ ਜਾ ਸਕਣ। ਜਦੋਂ ਅਸੀਂ ਰਾਤ ਵੇਲੇ ਅਕਾਸ਼ ਦੇਖਦੇ ਹਾਂ, ਅਸੀਂ ਮੁਢਲੇ ਤੌਰ ਤੇ ਸਾਰੇ ਸਪੇਸ ਸਮੇਂ ਵਿਚਲੀਆਂ ਸਿਰਫ ਭੂਤਕਾਲ ਦੀਆਂ ਪ੍ਰਕਾਸ਼ ਕੋਨਾਂ ਹੀ ਦੇਖਦੇ ਹਾਂ।
- ‘ਹੋਰ ਜਗਹ ਦੋ ਪ੍ਰਕਾਸ਼ ਕੋਨਾਂ ਦਰਮਿਆਨ ਦਾ ਖੇਤਰ ਹੈ। ਕਿਸੇ ਇੱਕ ਦਰਸ਼ਕ ਦੇ ‘ਹੋਰ ਜਗਹ’ ਵਿੱਚ ਵਾਲੇ ਬਿੰਦੂ ਉਸ ਦਰਸ਼ਕ ਲਈ ਪਹੁੰਦ ਤੋਂ ਬਾਹਰ ਹੁੰਦੇ ਹਨ; ਸਿਰਫ ਭੂਤਕਾਲ ਵਿਚਲੇ ਬਿੰਦੂ ਹੀ ਦਰਸ਼ਕ ਨੂੰ ਸਿਗਨਲ ਭੇਜ ਸਕਦੇ ਹਨ। ਸਧਾਰਨ ਪ੍ਰਯੋਗਸ਼ਾਲਾ ਦੇ ਤਜੁਰਬੇ ਵਿੱਚ, ਸਾਂਝੀਆਂ ਯੂਨਿਟਾਂ ਅਤੇ ਨਾਪਣ ਦੇ ਤਰੀਕੇ ਵਰਤਦੇ ਹੋਏ, ਇਹ ਲੱਗ ਸਕਦਾ ਹੈ ਕਿ ਅਸੀਂ ਵਰਤਮਾਨ ਵੱਲ ਦੇਖ ਰਹੇ ਹਾਂ, ਪਰ ਅਸਲ ਵਿੱਚ ਹਮੇਸ਼ਾ ਹੀ ਪ੍ਰਕਾਸ਼ ਨੂੰ ਸੂਚਨਾ ਪ੍ਰਸਾਰ ਕਰਨ ਲਈ ਇੱਕ ਦੇਰੀ ਲਗਦੀ ਹੈ। ਉਦਾਹਰਣ ਵਜੋਂ, ਅਸੀਂ ਸੂਰਜ ਨੂੰ 8 ਮਿੰਟ ਬਾਦ ਦੇਖਦੇ ਹਾਂ, ਨਾ ਕਿ ਜਿਵੇਂ ਇਹ ਹੁਣੇ ਹੁਣੇ ਹੁੰਦਾ ਹੈ। ਗਲੇਲੀਅਨ/ਨਿਊਟੋਨੀਅਨ ਥਿਊਰੀ ਤੋਂ ਉਲਟ, ‘ਹੋਰ ਜਗਹ’ ਸੰਘਣਾ ਖੇਤਰ ਹੁੰਦਾ ਹੈ। ਇਹ 3-ਅਯਾਮੀ ਘਣਫਲ ਨਹੀਂ ਹੁੰਦਾ ਸਗੋਂ ਇਹ ਇੱਕ 4-ਅਯਾਮੀ ਸਪੇਸ ਸਮੇਂ ਦਾ ਖੇਤਰ ਹੁੰਦਾ ਹੈ।
- ‘ਹੋਰ ਜਗਹ’ ਵਿੱਚ ਸਮਕਾਲੀਨ (ਤੁੰਰਤ ਹੋਣ ਵਾਲੀ) ‘ਹਾਈਪਰਪਲੇਨ’ ਸ਼ਾਮਿਲ ਹੁੰਦੀ ਹੈ, ਜੋ ਕਿਸੇ ਦਿੱਤੇ ਹੋਏ ਦਰਸ਼ਕ ਲਈ ਅਜਿਹੀ ਸਪੇਸ ਦੁਆਰਾ ਦਰਸਾਈ ਜਾਂਦੀ ਹੈ ਜੋ ਉਸਦੀ ਸੰਸਾਰ ਰੇਖਾ ਤੋਂ ਹਾਈਪਰਬੋਲਿਕ-ਔਰਥੋਗੋਨਲ (ਕਿਸੇ ਦਿੱਤੇ ਹਾਇਪਰਬੋਲੇ ਦੀ ਅਨੰਤ-ਸਪਰਸ਼ ਰੇਖਾ ਦੁਆਲੇ ਇੱਕ ਦੂਜੇ ਦੀ ਪਰਛਾਈਂ) ਹੁੰਦੀ ਹੈ। ਇਹ ਸੱਚਮੁੱਚ 3-ਅਯਾਮੀ ਹੁੰਦੀ ਹੈ, ਬੇਸ਼ੱਕ ਚਿੱਤਰ ਵਿੱਚ ਇਹ ਇੱਕ 2-ਸਤਹਿ ਵਾਲੀ ਹੋਵੇਗੀ ਕਿਉਂਕਿ ਸਾਨੂੰ ਸਮਝਣਯੋਗ ਬਣਾਉਣ ਲਈ ਇੱਕ ਅਯਾਮ ਸੁੱਟਣਾ ਪੈਂਦਾ ਹੈ। ਭਾਵੇਂ ਵੱਖਰੇ ਵੱਖਰੇ ਦਰਸ਼ਕਾਂ ਲਈ, ਕਿਸੇ ਦਿੱਤੀ ਸਪੇਸ ਸਮਾਂ ਘਟਨਾ ਲਈ ਪ੍ਰਕਾਸ਼ ਕੋਨਾਂ ਇੱਕੋ ਜਿਹੀਆਂ ਹੁੰਦੀਆਂ ਹਨ, ਫੇਰ ਵੀ ਵੱਖਰੀਆਂ ਵਿਲੌਸਟੀਆਂ ਨਾਲ ਪਰ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਘਟਨਾ-ਬਿੰਦੂ ਤੇ ਮਿਲਦੀਆਂ ਸੰਸਾਰ-ਰੇਖਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜੋ ਇੱਕ ਦੂਜੀ ਨੂੰ ਇੱਕ ਅਜਿਹੇ ਕੋਣ ਤੇ ਕੱਟਦੀਆਂ ਹਨ ਜੋ ਉਹਨਾਂ ਦੀਆਂ ਤੁਲਨਾਤਮਿਕ ਵਿਲੌਸਟੀਆਂ ਰਾਹੀ ਨਿਰਧਿਰਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਅਤੇ ਇਸੇ ਲਈ ਉਹ ਵੱਖਰੇ ਵੱਖਰੇ ਹਾਈਪਰਪਲੇਨਜ਼ ਰੱਖਦੀਆਂ ਹਨ।
- ਵਰਤਮਾਨ ਦਾ ਅਕਸਰ ਅਰਥ ਹੈ ਇੱਕੋ ਸਪੇਸ ਸਮਾਂ ਘਟਨਾ ਨੂੰ ਲੈਣਾ।
ਸਮਕਾਲੀਨ ਹਾਈਪਰਪਲੇਨ
[ਸੋਧੋ]ਕਿਉਂਕਿ ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਇੱਕ ਵਿਲੌਸਟੀ 4-ਵੈਕਟਰ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਦੀ ਹੈ ਜੋ ਸਮੇਂ-ਵਰਗਾ ਹੈ, ਇਸਲਈ ਮਿੰਕੋਵਸਕੀ ਫੌਮ ਇੱਕ ਰੇਖਿਕ ਫੰਕਸ਼ਨ ਨੂੰ ਦੁਆਰਾ ਨਿਰਧਾਰਿਤ ਕਰਦੀ ਹੈ। ਮੰਨ ਲਓ N ਇਸ ਰੇਖਿਕ ਫੰਕਸ਼ਨ ਦੀ ‘ਨੱਲ ਸਪੇਸ’ (null space) ਹੈ। ਫੇਰ N ਨੂੰ v ਦੇ ਸਬੰਧ ਵਿੱਚ ਸਮਕਾਲੀਨ ਹਾਈਪਰਪਲੇਨ ਕਿਹਾ ਜਾਵੇਗਾ। ਸਮਕਾਲੀਨਤਾ ਦੀ ਰੀਲੇਟੀਵਿਟੀ ਇੱਕ ਕਥਨ ਹੈ ਕਿ N ਦੀ ਨਿਰਭਰਤਾ v ਤੇ ਹੈ। ਸੱਚਮੁੱਚ, N, η ਦੇ ਸਬੰਧ ਵਿੱਚ v ਦਾ ਔਰਥੋਗੋਨਲ ਪੂਰਕ ਹੈ। ਜਦੋਂ ਦੋ ਸੰਸਾਰ ਰੇਖਾਵਾਂ u ਅਤੇ w ਦਾ ਰਾਹੀਂ ਆਪਸੀ ਸਬੰਧ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ, ਫੇਰ ਉਹ ਇੱਕੋ ਸਮਕਾਲੀਨ ਹਾਈਪਰਪਲੇਨ ਸਾਂਝਾ ਰੱਖਦੀਆਂ ਹਨ। ਇਹ ਹਾਈਪਰਪਲੇਨ ਗਣਿਤਿਕ ਤੌਰ ਤੇ ਮੌਜੂਦ ਹੁੰਦਾ ਹੈ, ਪਰ ਰੀਲੇਟੀਵਿਟੀ ਵਿੱਚ ਭੌਤਿਕੀ ਸਬੰਧ ਪ੍ਰਕਾਸ਼ ਦੁਆਰਾ ਸੂਚਨਾ ਦੀ ਗਤੀ ਮੰਗਦੇ ਹਨ। ਉਦਾਹਰਨ ਵਜੋਂ, ਕੂਲੌਂਬ ਦੇ ਨਿਯਮ ਦੁਆਰਾ ਦਰਸਾਇਆ ਪ੍ਰੰਪਰਾਗਤ ਇਲੈਕਟ੍ਰੋ-ਸਟੈਟਿਕ ਬਲ ਇੱਕ ਸਮਕਾਲੀਨ ਹਾਈਪਰਪਲੇਨ ਵਿੱਚ ਚਿਤ੍ਰਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਪਰ ਚਾਰਜ ਅਤੇ ਬਲ ਦੇ ਤੁਲਨਾਤਮਿਕ ਸਬੰਧ ਮੰਦ ਪੁਟੈਂਸ਼ਲ ਮੰਗਦੇ ਹਨ।
ਆਮ ਰੀਲੇਟੀਵਿਟੀ ਵਿੱਚ ਸੰਸਾਰ ਰੇਖਾਵਾਂ
[ਸੋਧੋ]ਜਨਰਲ ਰਿਲੇਟੀਵਿਟੀ ਵਿੱਚ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਦੀ ਵਰਤੋਂ ਮੁਢਲੇ ਤੌਰ ਤੇ ਸਪੈਸ਼ਲ ਰੀਲੇਟੀਵਿਟੀ ਵਾਂਗ ਹੀ ਹੈ, ਸਿਰਫ ਇੰਨਾ ਅੰਤਰ ਹੈ ਕਿ ਸਪੇਸ ਸਮਾਂ ਮੋੜਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਇੱਕ ਮੀਟ੍ਰਿਕ ਮੌਜੂਦ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਸਦੀ ਯੰਤਰਾਵਲੀ ਆਈਨਸਟਾਈਨ ਦੀਆਂ ਫੀਲਡ ਸਮੀਕਰਨਾਂ ਨਾਲ ਨਿਰਧਾਰਿਤ ਹੁੰਦੀ ਹੈ ਜੋ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਪੁੰਜ ਵੰਡ ਦੇ ਨਿਰਭਰ ਹੁੰਦੀਆਂ ਹਨ। ਫੇਰ ਮੀਟ੍ਰਿਕ ਪ੍ਰਕਾਸ਼-ਵਰਗੀਆਂ(ਨੱਲ), ਸਪੇਸ-ਵਰਗੀਆਂ ਅਤੇ ਸਮੇਂ ਵਰਗੀਆਂ ਵਕਰਾਂ ਪਰਿਭਾਸ਼ਿਤ ਕਰਦਾ ਹੈ। ਨਾਲ ਹੀ, ਜਨਰਲ ਰੀਲੇਟੀਵਿਟੀ ਵਿੱਚ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਸਮੇਂ-ਵਰਗੀਆਂ ਵਕਰਾਂ ਹਨ, ਜਿੱਥੇ ਸਮੇਂ-ਵਰਗੀਆਂ ਵਕਰਾਂ ਪ੍ਰਕਾਸ਼-ਕੋਨ ਦੇ ਵਿੱਚ ਡਿੱਗਦੀਆਂ ਹਨ। ਫੇਰ ਵੀ, ਇੱਕ ਪ੍ਰਕਾਸ਼ ਕੋਨ ਸਮੇਂ ਦੇ ਧੁਰੇ ਦੁਆਲੇ ਜਰੂਰੀ ਨਹੀਂ ਕਿ 45 ਡਿਗਰੀ ਤੇ ਝੁਕੀ ਹੋਵੇ। ਫੇਰ ਵੀ, ਇਹ ਚੁਣੇ ਹੋਏ ਨਿਰਦੇਸ਼- ਅੰਕ ਸਿਸਟਮ ਦਾ ਇੱਕ ਬਣਾਵਟੀ-ਸੱਚ ਹੁੰਦਾ ਹੈ, ਅਤੇਕਨਰਲ ਰੀਲੇਟੀਵਿਟੀ ਦੀ ਨਿਰਦੇਸ਼-ਅੰਕ ਦੀ ਮਨਚਾਹੀ ਅਜ਼ਾਦੀ (diffeomorphism invariance) ਪਰਿਵਰਤਿਤ ਕਰਦਾ ਹੈ। ਕੋਈ ਵੀ ਸਮੇਂ ਵਰਗੀ ਵਕਰ ਇੱਕ ਜੁੜਿਆ ਦਰਸ਼ਕ (comoving observer) ਸਵੀਕਾਰ ਕਰਦੀ ਹੈ ਜਿਸਦਾ ਸਮਾ ਧੁਰਾ ਉਸ ਵਕਰ ਨਾਲ ਸਬੰਧਿਤ ਹੁੰਦਾ ਹੈ, ਅਤੇ, ਕਿਉਂਕਿ ਕਿਸੇ ਦਰਸ਼ਕ ਨੂੰ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰ ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੁੰਦਾ, ਅਸੀਂ ਹਮੇਸ਼ਾ ਹੀ ਇੱਕ ਸਥਾਨਕ ਨਿਰਦੇਸ਼-ਅੰਕ ਸਿਸਟਮ ਖੋਜ ਸਕਦੇ ਹਾਂ ਜਿਸ ਵਿੱਚ ਪ੍ਰਕਾਸ਼ ਕੋਨਾਂ ਸਮੇਂ ਦੇ ਧੁਰੇ ਤੋਂ 45 ਡਿਗਰੀ ਤੇ ਝੁਕੀਆਂ ਹੋਣ। ਉਦਾਹਰਨ ਵਜੋਂ ਐਡਿੰਗਟਨ-ਫਿੰਕੇਲਸਟਾਈਨ ਨਿਰਦੇਸ਼ ਅੰਕਾਂ ਨੂੰ ਦੇਖੋ।
ਮੁਕਤ- ਡਿੱਗਦੇ ਕਣਾਂ ਜਾਂ ਵਸਤੂਆਂ ਦੀਆਂ ਸੰਸਾਰ ਰੇਖਾਵਾਂ (ਜਿਵੇਂ ਸੂਰਜ ਦੁਆਲੇ ਗ੍ਰਹਿ ਜਾਂ ਸਪੇਸ ਵਿੱਚ ਇੱਕ ਸਪੇਸਯਾਤਰੀ) ਨੂੰ ਜੀਓਡੈਸਿਕਸ (geodesics) ਕਿਹਾ ਜਾਂਦਾ ਹੈ।
ਸਾਹਿਤ ਵਿੱਚ ਸੰਸਾਰ ਰੇਖਾਵਾਂ
[ਸੋਧੋ]ਇਨਸਾਨੀ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਦਾ ਇੱਕ ਮਸ਼ਹੂਰ ਵਿਵਰਣ J. C. Fields ਦੁਆਰਾ ਯੂਨੀਵਰਸਿਟੀ ਔਫ ਟੋਰਾਂਟੋ ਵਿੱਚ ਰੀਲੇਟੀਵਿਟੀ ਦੇ ਸ਼ੁਰੂਆਤੀ ਦਿਨਾਂ ਵਿੱਚ ਦਿੱਤਾ ਗਿਆ। ਜਿਵੇਂ ਟੋਰਾਂਟੋ ਲਾਇਅਰ ਮੌਰਮਨ ਰੌਬਰਸਟਨ ਨੇ ਦਰਸਾਇਆ:
ਰੌਅਲ ਕੈਨੇਡੀਅਨ ਇੰਸਟੀਚਿਊਟ ਵਿਖੇ ਸ਼ਨੀਵਾਰ ਸ਼ਾਮ ਦੇ ਲੈਕਚਰਾਂ ਵਿੱਚੋਂ ਇੱਕ ਵਿੱਚ ਮੈਨੂੰ J. C. Fields ਦਾ ਲੈਕਚਰ ਯਾਦ ਹੈ। ਇਹ ਇੱਕ ਗਣਿਤਿਕ ਅਨੁਮਾਨ ਦੇ ਰੂਪ ਵਿੱਚ ਮਸ਼ਹੂਰ ਕੀਤਾ ਗਿਆ ਸੀ- ਅਤੇ ਇਹ ਸੀ ਵੀ। ਅਭਿਆਸ ਦਾ ਹਿੱਸਾ ਕੁੱਝ ਇਸ ਤਰਾਂ ਸੀ: ਉਸਨੇ ਦਿਖਾਇਆ ਕਿ, ਆਪਣੇ ਜਨਮ ਤੋਂ ਸ਼ੁਰੂ ਕਰਕੇ, ਹਰੇਕ ਇਨਸਾਨ ਕੋਲ ਇੱਕ ਰੂਹਾਨੀ ਲੰਬੇ ਰੇਸ਼ੇ ਜਾਂ ਬੰਨੇ ਹੋਏ ਧਾਗੇ ਨਾਲ ਦਿੱਵਯ-ਜੋਤ ਹੁੰਦੀ ਹੈ, ਜਿਸਨੇ ਉਸਦੇ ਪਿੱਛੇ ਉਸਦੀ ਸਾਰੀ ਜਿੰਦਗੀ ਬਿਤਾਈ ਹੁੰਦੀ ਹੈ। ਫੇਰ ਉਹ ਜਟਿਲ ਉਲਝਣ ਵਾਲੀ ਐਨਟੈਂਗਲਮੈਂਟ ਦੇ ਵਿਵਰਣ ਲਈ ਕਲਪਨਾ ਵੱਲ ਚਲਾ ਗਿਆ ਜਿਸ ਵਿੱਚ ਹਰੇਕ ਇਨਸਾਨ ਜਵਾਨੀ ਦੀਆਂ ਸਧਾਰਨ ਉਲਝਣਾਂ ਦਾ ਬਾਸ ਦੀ ਜਿੰਦਗੀ ਦੀ ਗੰਢਾਂ ਨਾਲ ਤੁਲਨਾ ਕਰਦਾ ਹੋਇਆ ਆਪਣੇ ਹੋਰਾਂ ਨਾਲ ਰਿਸ਼ਤਿਆਂ ਰਾਹੀਂ ਸ਼ਾਮਿਲ ਹੁੰਦਾ ਹੈ।
ਕਿਉਂਕਿ ਉਹ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਨੂੰ ਜਿਆਦਾ ਸਰਲ ਕਰਕੇ 1-ਅਯਾਮੀ ਸਮਾਂ ਰੇਖਾਵਾਂ ਵਿੱਚ ਬਦਲਦੇ ਹਨ, ਜੋ 4-ਅਯਾਮੀ ਸਪੇਸ ਸਮੇਂ ਨੂੰ ਪਾਰ ਕਰਦੀਆਂ ਹਨ, ਲਗਭਗ ਸਾਰੀਆਂ ਵਕਤ ਦੀ ਯਾਤਰਾ ਕਰਨ ਵਾਲੀਆਂ ਕਲਪਿਤ ਵਿਗਿਆਨ ਦੀਆਂ ਕਹਾਣੀਆਂ ਅਸਲ ਵਿੱਚ ਇੱਛਾਧਾਰੀ ਅਨੁਮਾਨਾਂ ਦੀਆਂ ਕਹਾਣੀਆਂ ਹਨ। ਕੁੱਝ ਯੰਤਰ ਜਾਂ ਸੁੱਪਰ ਸ਼ਕਤੀਮਾਨ ਇਨਸਾਨ ਆਮ ਤੌਰ ਤੇ ਦਿਖਾਏ ਜਾਂਦੇ ਹਨ ਜੋ ਵਕਤ ਵਿੱਚ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਨਿਕਲਦੇ ਦਿਖਾਏ ਜਾਂਦੇ ਹਨ, ਅਤੇ ਘੱਟ ਜਾਂ ਬਗੈਰ ਵਿਸ਼ੇ ਨੂੰ ਪਿੱਛੇ ਛੱਡੇਮ ਵਕਤ ਵਿੱਚ ਕਿਸੇ ਹੋਰ ਬਿੰਦੂ ਤੇ ਪਹੁੰਚਦੇ ਦਿਖਾਏ ਜਾਂਦੇ ਹਨ- ਪਰ ਉਸੇ ਸਪੇਸ ਦੇ ਜੀਊਗਰਾਫਿਕ ਬਿੰਦੂ ਤੇ, ਆਮਤੌਰ ਤੇ ਕਿਸੇ ਵਰਕਸ਼ੌਪ ਵਿੱਚ ਜਾਂ ਕਿਸੇ ਇਤਿਹਾਸਿਕ ਜਗਹ ਤੇ। ਫੇਰ ਵੀ, ਅਸਲੀਅਤ ਵਿੱਚ ਗ੍ਰਹਿ, ਇਸਦਾ ਸੂਰਜ ਸਿਸਟਮ, ਅਤੇ ਇਸਦੀ ਗਲੈਕਸੀ ਪਹੁੰਚਣ ਤੇ ਵਿਸ਼ਾਲ ਵੱਖਰੇ ਸਥਾਨਿਕ ਸਥਾਨਾਂ ਤੇ ਹੋਣਗੇ। ਇਸਲਈ, ਵਕਤ ਦੀ ਯਾਤਰਾ ਦੀ ਯੰਤਰਾਵਲੀ ਨੂੰ ਤੁਰੰਤ ਟੈਲੀਪੋਰਟੇਸ਼ਨ, ਅਨੰਤ ਤੌਰ ਤੇ ਸਹੀ ਸਹੀ ਅਤੇ ਤੁਰੰਤ ਅੰਤਿਮ 3- ਅਯਾਮੀ ਸਥਾਨ ਦਾ ਪ੍ਰਬੰਧ ਹੋਵੇ, ਰੇਖਿਕ ਆਵੇਗ, ਅਤੇ ਕੋਣਿਕ ਆਵੇਗ ਵੀ ਮੋਹੱਈਆ ਕਰਵਾਉਣਾ ਚਾਹੀਦਾ ਹੈ।
ਸੰਸਾਰ ਰੇਖਾਵਾਂ Jeffrey Rowland' ਦੇ ਵੈੱਬਕੌਮਿਕ Wigu Adventures ਵਿੱਚ "Magical Adventures in Space" ਦੇ ਹਿੱਸੇ ਵਜੋਂ ਦਿਸੀਆਂ, ਜਿਸ ਵਿੱਚ ਟੋਪਾਟੋ ਪੋਟੈਟੋ ਅਤੇ ਸ਼ੈਰਿੱਫ ਪੌਨੀ ਅਚਾਨਕ ਧੁਮਕੇਤੂਆਂ ਦੁਆਰਾ ਧਰਤੀ ਦੀ ਸ਼ੁਰੂਆਤੀ ਰਚਨਾ ਵੇਲੇ ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਡਲੀਟ ਕਰ ਦਿੰਦੇ ਹਨ ਜਿਸ ਨਾਲ ਧਰਤੀ ਕਦੇ ਵੀ ਮੌਜੂਦ ਨਹੀਂ ਰਹੀ ਹੁੰਦੀ। ਉਸਦੇ ਵੈਬਕੌਮਿਕ ਅਨੁਸਾਰ, ਇੱਕ ਸੰਸਾਰ ਰੇਖਾ ਦੀ ਗਣਨਾ ਕਰਨਾ ‘ਸੁਣਨ ਜਿੰਨਾ ਸਰਲ’ ਹੈ, ਅਤੇ ਵਿਸ਼ੇਸ਼ ਸੰਸਾਰ ਰੇਖਾ ਨੂੰ ਖਤਮ ਕਰਨਾ ਇੱਕ ਕਾਲ ਕਰਕੇ ਸੰਸਾਰ ਰੇਖਾ ਵਿੱਚ ਦਾਖਲ ਹੋ ਕੇ 3 ਨੰਬਰ ਦੱਬਣ ਨਾਲ ਹੋ ਜਾਂਦਾ ਹੈ।
ਲੇਖਕ Oliver Franklin ਨੇ 2008 ਵਿੱਚ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਨਾਮਕ ਕਲਪਿਤ ਵਿਗਿਆਨ ਛਪਵਾਇਆ ਜਿਸ ਵਿੱਚ ਉਸਨੇ laymen ਦੀ ਕਲਪਨਾ ਦਾ ਇੱਕ ਸਰਲ ਵਿਵਰਣ ਦਿੱਤਾ।
ਇੱਕ ਛੋਟੀ ਕਹਾਣੀ ਜਿਸਦਾ ਨਾਮ Life-Line ਹੈ, ਵਿੱਚ ਲੇਖਕ Robert A. Heinlein ਨੇ ਇੱਕ ਇਨਸਾਨ ਦੀ ਸੰਸਾਰ ਰੇਖਾ ਦਰਸਾਈ।
ਉਸਨੇ ਰਿਪੋਰਟਰਾਂ ਵਿੱਚੋਂ ਇੱਕ ਅੱਗੇ ਕਦਮ ਪੁੱਟੇ। ‘ਮੰਨ ਲਓ ਅਸੀਂ ਤੁਆਨੂੰ ਉਦਾਹਰਨ ਵਜੋਂ ਲੈਂਦੇ ਹਾਂ। ਤੁਆਡਾ ਨਾਲ ਰੋਜਰਜ਼ ਹੈ, ਜਾਂ ਨਹੀਂ ਹੈ? ਬਹੁਤ ਚੰਗਾ, ਰੋਜ਼ਰਜ਼, ਤੂੰ ਇੱਕ ਸਪੇਸ ਸਮਾਂ ਘਟਨਾ ਹੈਂ ਜਿਸਦਾ ਅਰਸਾ ਚਾਰ ਤਰੀਕਿਆਂ ਨਾਲ ਹੈ। ਤੂੰ ਸਹੀ ਸਹੀ 6 ਫੁੱਟ ਲੰਬਾ ਨਹੀਂ ਹੈ, ਤੂੰ ਲਗਭਗ 20 ਇੰਚ ਚੌੜਾ ਹੈਂ ਅਤੇ ਸ਼ਾਇਦ 10 ਇੰਚ ਮੋਟਾ। ਵਕਤ ਵਿੱਚ, ਇਸ ਸਪੇਸ ਸਮਾਂ ਘਟਨਾ ਦਾ ਹੋਰ ਹਿੱਸਾ ਜਿਆਦਾ ਤੇਰੇ ਪਿੱਛੇ ਖਿੱਚਿਆ ਗਿਆ ਹੈ, ਜਿਸਦਾ ਸ਼ਾਇਦ 19-16 ਤੱਕ ਪਹੁੰਚਦਾ, ਹਿੱਸਾ ਅਸੀਂ ਵਕਤ ਦੇ ਧੁਰੇ ਤੇ ਇੱਥੇ ਕਰੌਸ ਸੈਕਸ਼ਨ 90 ਡਿਗਰੀ ਦੇ ਦੇਖਦੇ ਹਾਂ, ਅਤੇ ਮੋਟਾਈ ਵਰਤਮਾਮ ਜਿੰਨੀ ਹੀ ਹੈ। ਦੂਰ ਦੇ ਸਿਰੇ ਤੇ ਇੱਕ ਬੱਚਾ ਹੈ, ਖੱਟੇ ਦੁੱਧ ਨੂੰ ਸੁੰਘਦਾ ਹੋਇਆ ਅਤੇ ਆਪਣੀ ਛਾਤੀ ਤੇ ਰੱਖੇ ਛੋਟੇ ਕੱਪੜੇ ਤੇ ਆਪਣੇ ਖਾਣੇ ਦੀ ਲਾਰ ਸਿੱਟਦਾ ਹੋਇਆ। ਦੂਜੇ ਸਿਰੇ ਤੇ, ਸ਼ਾਇਦ, ਇੱਕ ਬੁੱਢਾ ਅਦਮੀ 19-80 ਵਿੱਚ ਕਿਸੇ ਜਗਹ।
‘ਇਸ ਸਪੇਸ ਸਮਾਂ ਘਟਨਾ ਬਾਰੇ ਸੋਚੋ ਜਿਸਨੂੰ ਅਸੀਂ ਰੋਜ਼ਰਜ਼ ਕਹਿੰਦੇ ਹਾਂ ਜੋ ਇੱਕ ਲੰਬੇ ਗੁਲਾਬੀ ਕੀੜੇ ਵਰਗੀ, ਸਾਲਾਂ ਤੱਕ ਨਿਰੰਤਰ, ਇੱਕ ਸਿਰਾ ਮਾਤਾ ਦੇ ਗਰਭ ਵਿੱਚ, ਅਤੇ ਦੂਜਾ ਸਿਰਾ ਕਬਰ ਵਿੱਚ ...।’
Heinlein ਦੇ Methuselah's Children ਵਿੱਚ ਸ਼ਬਦ ਵਰਤਿਆ ਗਿਆ, ਜਿਵੇਂ James Blish ਦੀ The Quincunx of Time ਵਿੱਚ ("ਬੀਪ"ਤੋਂ ਫੈਲਾਇਆ ਹੋਇਆ) ਵੀ ਇਹ ਸ਼ਬਦ ਵਰਤਿਆ ਗਿਆ।
Steins;Gate ਨਾਮਕ ਇੱਕ visual ਨਾਵਲ ਵਿੱਚ ਜੋ 5pb. ਦੁਆਰਾ ਪ੍ਰੋਡਿਊਸ ਕੀਤਾ ਗਿਆ ਵੀ ਸੰਸਾਰ ਰੇਖਾ ਦੀ ਤਬਦੀਲੀ ਦੀ ਕਹਾਣੀ ਦੱਸਦਾ ਹੈ। hypothetical science ADVਦੇ ਨਾਮ ਨਾਲ ਇਸਦੀਆਂ ਲੜੀਆਂ ਦੇ ਕੰਮ ਨੇ ਵੀ ਇਸ ਵਿਚਾਰ ਨੂੰ ਦਰਸਾਇਆ ਹੈ।




