ਕਰੌਸ ਪ੍ਰੋਡਕਟ

ਗਣਿਤ ਅਤੇ ਵੈਕਟਰ ਕੈਲਕੁਲਸ ਵਿੱਚ, ਕਰੌਸ ਪ੍ਰੋਡਕਟ ਜਾਂ ਵੈਕਟਰ ਪ੍ਰੋਡਕਟ (ਕੁੱਝ ਮੌਕਿਆਂ ਤੇ ਰੇਖਾਗਣਿਤਿਕ ਮਹੱਤਤਾ ਤੇ ਜੋਰ ਦੇਣ ਲਈ ਖੇਤਰ ਗੁਣਨਫਲ ਵੱਲ ਨਿਰਦੇਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ), ਤਿੰਨ-ਡਾਇਮੈਨਸ਼ਨਲ ਸਪੇਸ (R3) ਵਿੱਚ ਦੋ ਵੈਕਟਰਾਂ ਉੱਤੇ ਇੱਕ ਬਾਇਨਰੀ (ਦੋ-ਰੇਖਿਕ) ਓਪਰੇਸ਼ਨ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਸਨੂੰ ਚਿੰਨ੍ਹ × ਨਾਲ ਲਿਖਿਆ ਜਾਂਦਾ ਹੈ। ਦੋ ਰੇਖਿਕ ਤੌਰ 'ਤੇ ਆਤਮਨਿਰਭਰ ਵੈਕਟਰ a ਅਤੇ b ਦਿੱਤੇ ਹੋਣ ਤੇ ਕਰੌਸ ਪ੍ਰੋਡਕਟ a × b, ਇੱਕ ਅਜਿਹਾ ਵੈਕਟਰ ਬਣੇਗਾ ਜੋ ਦੋਹਾਂ ਤੋਂ ਪਰਪੈਂਡੀਕਿਊਲਰ (ਸਮਕੋਣ) ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਸ ਕਰ ਕੇ ਉਹਨਾਂ ਨੂੰ ਰੱਖਣ ਵਾਲੀ ਪਲੇਨ (ਸਤਹਿ) ਤੋਂ ਨੌਰਮਲ (90 ਡਿਗਰੀ ਤੇ) ਹੁੰਦਾ ਹੈ। ਇਸ ਦੀਆਂ ਗਣਿਤ, ਭੌਤਿਕ ਵਿਗਿਆਨ, ਇੰਜੀਨਿਅਰਿੰਗ, ਅਤੇ ਕੰਪਿਊਟਰ ਪ੍ਰੋਗਰਾਮਿੰਗ ਵਿੱਚ ਬਹੁਤ ਸਾਰੀਆਂ ਐਪਲੀਕੇਸ਼ਨਾਂ (ਉਪਯੋਗ) ਹਨ। ਇਸਨੂੰ ਡੌਟ ਪ੍ਰੋਡਕਟ (ਪ੍ਰੋਜੈਕਸ਼ਨ ਗੁਣਨਫਲ) ਨਹੀਂ ਸਮਝਣਾ ਚਾਹੀਦਾ।
ਪਰਿਭਾਸ਼ਾ
[ਸੋਧੋ]
ਕਰੌਸ ਪ੍ਰੋਡਕਟ ਨੂੰ ਇਸ ਫਾਰਮੂਲੇ ਦੁਆਰਾ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ[1][2]

ਨਾਮ
[ਸੋਧੋ]
ਕਰੋਸ ਪ੍ਰੋਡਕਟ ਦਾ ਹਿਸਾਬ ਲਗਾਉਣਾ
[ਸੋਧੋ]ਨਿਰਦੇਸ਼ਾਂਕ ਧਾਰਨਾ
[ਸੋਧੋ]
ਮੈਟ੍ਰਿਕਸ ਧਾਰਨਾ
[ਸੋਧੋ]
ਕਰੌਸ ਪ੍ਰੋਡਕਟ ਨੂੰ ਰਸਮੀ ਤੌਰ 'ਤੇ ਵੀ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ[note 1] determinant:
ਇਸ ਡਿਟ੍ਰਮੀਨੈਂਟ ਨੂੰ ਸਾਰੁੱਸ ਦੇ ਨਿਯਮ ਦੀ ਬਰਤੋ ਕਰਦੇ ਹੋਏ ਪਤਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਜਾਂ ਕੋਫੈਕਟਰ ਪ੍ਰਸਾਰ ਦੀ ਵਰਤੋ ਨਾਲ ਵੀ ਪਤਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਸਾਰੁੱਸ ਨਿਯਮ ਨਿਯਮ ਵਰਤਦੇ ਹੋਏ, ਇਹ ਇਸ ਤਰ੍ਹਾਂ ਫੈਲਦਾ ਹੈ
ਕੋਫੈਕਟਰ ਫੈਲਾਓ ਵਰਤਦੇ ਹੋਏ ਪਹਿਲੀ ਕਤਾਰ ਦੇ ਨਾਲ ਦੀ ਦਿਸ਼ਾ ਦੀ ਜਗਹ, ਇਹ ਇਸ ਤਰ੍ਹਾਂ ਫੈਲਦਾ ਹੈ[3]
ਜੋ ਨਤੀਜਨ ਵੈਕਟਰਾਂ ਦੇ ਪੁਰਜੇ ਸਿੱਧੇ ਹੀ ਦੇ ਦਿੰਦਾ ਹੈ
ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ
[ਸੋਧੋ]ਰੇਖਾਗਣਿਤਿਕ ਅਰਥ
[ਸੋਧੋ]

ਅਲਜਬਰਿਕ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ
[ਸੋਧੋ]

ਡਿੱਫਰੈਂਟੀਏਸ਼ਨ
[ਸੋਧੋ]ਡਿੱਫਰੈਂਸ਼ੀਅਲ ਕੈਲਕੁਲਸ ਦਾ ਗੁਣਨਫਲ ਨਿਯਮ ਕਿਸੇ ਵੀ ਦੋ-ਰੇਖਿਕ ਓਪਰੇਸ਼ਨ ਤੇ ਲਾਗੂ ਹੋ ਜਾਂਦਾ ਹੈ, ਅਤੇ ਇਸਲਈ ਕਰੌਸ ਪ੍ਰੋਡਕਟ ਤੇ ਵੀ ਲਾਗੂ ਹੁੰਦਾ ਹੈ:
ਜਿੱਥੇ a ਅਤੇ b ਉਹ ਵੈਕਟਰ ਹਨ ਜੋ ਵਾਸਤਵਿਕ ਅਸਥਿਰਾਂਕ t ਉੱਤੇ ਨਿਰਭਰ ਕਰਦੇ ਹਨ।
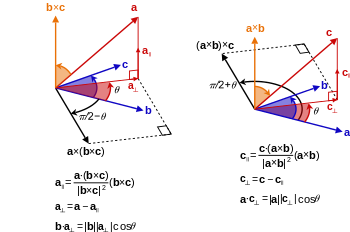
ਤੀਹਰਾ ਗੁਣਨਫਲ ਪ੍ਰਸਾਰ
[ਸੋਧੋ]ਬਦਲਵੀਂ ਫਾਤਮੂਲਾ ਵਿਓਂਤਬੰਦੀ
[ਸੋਧੋ]ਲਗਰਾਂਜ ਆਇਡੈਂਟਿਟੀ
[ਸੋਧੋ]ਰੋਟੇਸ਼ਨਾਂ ਦੇ ਅਤਿਸੂਖਮ ਜਨਰੇਟਰ
[ਸੋਧੋ]ਕਰੌਸ ਪ੍ਰੋਡਕਟ ਦਾ ਹਿਸਾਬ ਲਗਾਉਣ ਦੇ ਬਦਲਵੇਂ ਤਰੀਕੇ
[ਸੋਧੋ]ਮੈਟ੍ਰਿਕਸ ਗੁਣਾ ਵਿੱਚ ਪਰਿਵਰਤਨ
[ਸੋਧੋ]ਟੈਂਸਰਾਂ ਵਾਸਤੇ ਸੂਚਕਾਂਕ ਚਿੰਨ੍ਹ
[ਸੋਧੋ]ਯਾਦਸ਼ਕਤੀ ਸ਼ਹਾਇਕ
[ਸੋਧੋ]ਆਰਪਾਰ ਦ੍ਰਿਸ਼
[ਸੋਧੋ]ਉਪਯੋਗ
[ਸੋਧੋ]ਹਿਸਾਬ-ਕਿਤਾਬੀ ਰੇਖਾਗਣਿਤ
[ਸੋਧੋ]ਐਂਗੁਲਰ ਮੋਮੈਂਟਮ ਅਤੇ ਟਾਰਕ
[ਸੋਧੋ]ਠੋਸ ਸਰੀਰ
[ਸੋਧੋ]ਲੌਰੰਟਜ਼ ਬਲ
[ਸੋਧੋ]ਫੁਟਕਲ
[ਸੋਧੋ]ਇੱਕ ਬਾਹਰੀ ਚੀਜ਼ ਦੇ ਰੂਪ ਵਿੱਚ ਕਰੌਸ ਪ੍ਰੋਡਕਟ
[ਸੋਧੋ]
ਕਰੌਸ ਪ੍ਰੋਡਕਟ ਅਤੇ ਮਰਜੀ ਦੀ ਦਿਸ਼ਾ
[ਸੋਧੋ]ਸਰਵ-ਸਧਾਰੀਕਰਨਾਂ
[ਸੋਧੋ]ਲਾਈ ਅਲਜਬਰਾ
[ਸੋਧੋ]ਕੁਆਟ੍ਰਨੀਔਨ
[ਸੋਧੋ]ਔਕਟਨੀਔਨ
[ਸੋਧੋ]ਵੈੱਜ ਪ੍ਰੋਡਕਟ
[ਸੋਧੋ]ਬਹੁਰੇਖਿਕ ਅਲਜਬਰਾ
[ਸੋਧੋ]ਸਕਿਊਸਮਿੱਟਰਿਕ ਮੈਟ੍ਰਿਕਸ
[ਸੋਧੋ]ਇਤਿਹਾਸ
[ਸੋਧੋ]ਇਹ ਵੀ ਦੇਖੋ
[ਸੋਧੋ]- ਬਾਇਵੈਕਟਰ
- ਕਾਰਟੀਜ਼ੀਅਨ ਪ੍ਰੋਡਕਟ – ਦੋ ਸੈੱਟਾਂ ਦਾ ਇੱਕ ਗੁਣਨਫਲ
- ਡੌਟ ਪ੍ਰੋਡਕਟ
- ਬਾਹਰੀ ਅਲਜਬਰਾ
- ਮਲਟੀਪਲ ਕਰੌਸ ਪ੍ਰੋਡਕਟ –ਠਿੰਨ ਵੈਕਟਰਾਂ ਤੋਂ ਜਿਆਦਾ ਵਾਲੇ ਪ੍ਰੋਡਕਟ
- ਸੂਡੋਵੈਕਟਰ
- × (ਚਿੰਨ)
ਨੋਟਸ
[ਸੋਧੋ]- ↑ Here, “formal" means that this notation has the form of a determinant, but does not strictly adhere to the definition; it is a mnemonic used to remember the expansion of the cross product.
- ↑ Wilson 1901
- ↑ Dennis G. Zill; Michael R. Cullen (2006). "Definition 7.4: Cross product of two vectors". Advanced engineering mathematics (3rd ed.). Jones & Bartlett Learning. p. 324. ISBN 0-7637-4591-X.
- ↑ Dennis G. Zill; Michael R. Cullen (2006). "Equation 7: a × b as sum of determinants". cited work. Jones & Bartlett Learning. p. 321. ISBN 0-7637-4591-X.
- ↑ M. R. Spiegel; S. Lipschutz; D. Spellman (2009). Vector Analysis. Schaum's outlines. McGraw Hill. p. 29. ISBN 978-0-07-161545-7.
- Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. p. 134. ISBN 978-0-486-67766-8.
{{cite book}}: Invalid|ref=harv(help) - E. A. Milne (1948) Vectorial Mechanics, Chapter 2: Vector Product, pp 11 –31, London: Methuen Publishing.
- Wilson, Edwin Bidwell (1901). Vector Analysis: A text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. Yale University Press.
{{cite book}}: Invalid|ref=harv(help) - T. Levi-Civita; U. Amaldi (1949). Lezioni di meccanica razionale (in Italian). Zanichelli editore.
{{cite book}}: Unknown parameter|city=ignored (|location=suggested) (help)CS1 maint: unrecognized language (link)
ਬਾਹਰੀ ਲਿੰਕ
[ਸੋਧੋ]- Hazewinkel, Michiel, ed. (2001), "Cross product", ਗਣਿਤ ਦਾ ਵਿਸ਼ਵਕੋਸ਼, ਸਪਰਿੰਗਰ, ISBN 978-1-55608-010-4
- Weisstein, Eric W., ਪ੍ਰੋਡਕਟ.html "ਕਰੌਸ ਪ੍ਰੋਡਕਟ", ਗਣਿਤ-ਸੰਸਾਰ.
- A quick geometrical derivation and interpretation of cross products
- C.A. Gonano and R.E. Zich (2014). Cross product in N Dimensions - the doublewedge product, Polytechnic University of Milan, Italy.
- Z.K. Silagadze (2002). Multi-dimensional vector product. Journal of Physics. A35, 4949 Archived 2015-09-05 at the Wayback Machine. (it is only possible in 7-D space)
- Real and Complex Products of Complex Numbers
- An interactive tutorial Archived 2006-04-24 at the Wayback Machine. created at Syracuse University – (requires java)
- W. Kahan (2007). Cross-Products and Rotations in Euclidean 2- and 3-Space. University of California, Berkeley (PDF).





