ਕੁਆਂਟਮ ਲੌਜਿਕ ਗੇਟ
ਇਸ ਲੇਖ ਨੂੰ ਤਸਦੀਕ ਲਈ ਹੋਰ ਹਵਾਲੇ ਚਾਹੀਦੇ ਹਨ। (February 2018) |
ਕੁਆਂਟਮ ਕੰਪਿਊਟਿੰਗ ਵਿੱਚ, ਅਤੇ ਵਿਸ਼ੇਸ਼ ਤੌਰ ਤੇ ਕੰਪਿਊਟੇਸ਼ਨ ਦੇ ਕੁਆਂਟਮ ਸਰਕਟ ਮਾਡਲ ਵਿੱਚ, ਇੱਕ ਕੁਆਂਟਮ ਲੌਜਿਕ ਗੇਟ (ਜਾਂ ਸਰਲ ਤੌਰ ਤੇ ਕੁਆਂਟਮ ਗੇਟ), ਕਿਉਬਿਟਾਂ ਦੀ ਇੱਕ ਛੋਟੀ ਸੰਖਿਆ ਉੱਤੇ ਓਪਰੇਟ ਕਰਨ ਵਾਲਾ ਇੱਕ ਮੁਢਲਾ ਕੁਆਂਟਮ ਸਰਕਟ ਹੁੰਦਾ ਹੈ। ਇਹ ਓਸੇ ਤਰਾਂ ਕੁਆਂਟਮ ਸਰਕਟਾਂ ਦੇ ਬਿਲਡਿੰਗ ਬਲੌਕ ਹੁੰਦੇ ਹਨ ਜਿਵੇਂ, ਕਲਾਸੀਕਲ ਲੌਜਿਕ ਗੇਟ, ਪ੍ਰੰਪ੍ਰਿਕ ਡਿਜੀਟਲ ਸਰਕਟਾਂ ਲਈ ਬਿਲਡਿੰਗ ਬਲੌਕ ਹੁੰਦੇ ਹਨ।
ਕਈ ਕਲਾਸੀਕਲ ਲੌਜਿਕ ਗੇਟਾਂ ਤੋਂ ਉਲਟ, ਕੁਆਂਟਮ ਲੌਜਿਕ ਗੇਟ ਰਿਵਰਸੀਬਲ ਹੁੰਦੇ ਹਨ। ਫੇਰ ਵੀ, ਸਿਰਫ ਉਲਟਣ-ਯੋਗ ਗੇਟਾਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ ਕਲਾਸੀਕਲ ਕੰਪਿਊਟਿੰਗ ਕਰਨਾ ਸੰਭਵ ਹੈ। ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, ਉਲਟਣ-ਯੋਗ ਟੌਫੌਲੀ ਗੇਟ, ਅੰਸਿਲਾ ਬਿੱਟਾਂ ਨੂੰ ਵਰਤਣ ਦੀ ਕੀਮਤ ਉੱਤੇ ਅਕਸਰ, ਸਾਰੇ ਬੂਲਨ ਫੰਕਸ਼ਨ ਲਾਗੂ ਕਰ ਸਕਦਾ ਹੈ। ਟੌਫੌਲੀ ਗੇਟ ਇੱਕ ਸਿੱਧਾ ਕੁਆਂਟਮ ਸਮਾਨਤਾ ਵਾਲਾ ਬਦਲ ਰੱਖਦਾ ਹੈ, ਜੋ ਦਿਖਾਉਂਦਾ ਹੈ ਕਿ ਕੁਆਂਟਮ ਸਰਕਟ, ਕਲਾਸੀਕਲ ਸਰਕਟਾਂ ਦੁਆਰਾ ਕੀਤੇ ਜਾਣ ਵਾਲੇ ਸਾਰੇ ਕੰਮ ਕਰ ਸਕਦੇ ਹਨ।
ਪੇਸ਼ਕਾਰੀ
[ਸੋਧੋ]ਕੁਆਂਟਮ ਲੌਜਿਕ ਗੇਟਾਂ ਨੂੰ ਯੂਨਾਇਟ੍ਰੀ ਮੈਟ੍ਰਿਕਸਾਂ ਰਾਹੀਂ ਪੇਸ਼ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਗੇਟ ਦੀ ਇਨਪੁੱਟ ਅਤੇ ਆਊਟਪੁੱਟ ਵਿੱਚ ਕਿਉਬਿੱਟਾਂ ਦੀ ਸੰਖਿਆ ਲਾਜ਼ਮੀ ਤੌਰ ਤੇ; ਇੱਕ ਅਜਿਹੇ ਗੇਟ ਦੇ ਬਰਾਬਰ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਜੋ ਕਿਉਬਿੱਟਾਂ ਤੇ ਕ੍ਰਿਆ ਕਰਦਾ ਹੈ, ਜਿਸਨੂੰ ਇੱਕ ਯੁਨਾਇਟ੍ਰੀ ਮੈਟ੍ਰਿਕਸ ਦੁਆਰਾ ਪੇਸ਼ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਜਿਹੜੀਆਂ ਕੁਆਂਟਮ ਅਵਸਥਾਵਾਂ ਤੇ ਗੇਟ ਕ੍ਰਿਆ ਕਰਦੇ ਹਨ, ਉਹ ਕੰਪਲੈਕਸ ਅਯਾਮਾਂ ਅੰਦਰ ਵੈਕਟਰ ਹੁੰਦੇ ਹਨ। ਬੇਸ ਵੈਕਟਰ, ਨਾਪੇ ਜਾਣ ਤੇ ਸੰਭਵ ਨਤੀਜੇ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇੱਕ ਕੁਆਂਟਮ ਅਵਸਥਾ, ਇਹਨਾਂ ਨਤੀਜਿਆਂ ਦਾ ਇੱਕ ਰੇਖਿਕ ਮੇਲ ਹੁੰਦਾ ਹੈ। ਸਭ ਤੋਂ ਜਿਆਦਾ ਸਾਂਝੇ ਕੁਆਂਟਮ ਗੇਟ, ਇੱਕ ਜਾਂ ਦੋ ਕਿਉਬਿੱਟਾਂ ਦੀਆਂ ਸਪੇਸਾਂ ਉੱਤੇ ਓਪਰੇਟ ਕਰਦੇ ਹਨ, ਜਿਵੇਂ ਸਾਂਝੇ ਕਲਾਸੀਕਲ ਲੋਜਿਕ ਗੇਟ ਇੱਕ ਜਾਂ ਦੋ ਬਿੱਟਾਂ ਉੱਤੇ ਓਪਰੇਟ ਕਰਦੇ ਹਨ।
ਕਿਸੇ ਇਕਲੌਤੇ ਕਿਉਬਿੱਟ ਦੀ ਵੈਕਟਰ ਪੇਸ਼ਕਾਰੀ ਇਹ ਹੁੰਦੀ ਹੈ:
- ,
ਕਿਸੇ ਦੋ ਕਿਉਬਿੱਟ ਦੀ ਵੈਕਟਰ ਪੇਸ਼ਕਾਰੀ ਇਹ ਹੁੰਦੀ ਹੈ:
- ,
ਕਿਸੇ ਖਾਸ ਕੁਆਂਟਮ ਅਵਸਥਾ ਉੱਤੇ ਗੇਟ ਦੀ ਕ੍ਰਿਆ ਨੂੰ ਵੈਕਟਰ ਨਾਲ ਗੁਣਾ ਕਰਕੇ ਖੋਜਿਆ ਜਾ ਸਕਦਾ ਹੈ ਜੋ: ਗੇਟ ਨੂੰ ਪੇਸ਼ ਕਰਨ ਵਾਲੇ ਮੈਟ੍ਰਿਕਸ ਰਾਹੀਂ ਪੇਸ਼ ਹੋਣ ਵਾਲੀ ਅਵਸਥਾ ਨੂੰ ਪੇਸ਼ ਕਰਦੀ ਹੈ।
ਇਤਿਹਾਸ
[ਸੋਧੋ]ਕੁਆਂਟਮ ਗੇਟਾਂ ਦੀ ਵਰਤਮਾਨ ਧਾਰਨਾ ਬਾਰਾਂਕੋ, ਦੁਆਰਾ[1] ਫੇਨਮੇਨ ਦੁਆਰਾ ਪੇਸ਼ ਕੀਤੀਆਂ ਧਾਰਨਾਵਾਂ ਬਣਾਉਂਦੇ[2] ਹੋਏ ਵਿਕਸਿਤ ਕੀਤੀ ਗਈ ਸੀ।
ਮਹੱਤਵਪੂਰਨ ਉਦਾਹਰਨਾਂ
[ਸੋਧੋ]
ਹਦਮਰਦ (H) ਗੇਟ
[ਸੋਧੋ]ਹਦਮਰਦ ਗੇਟ ਕਿਸੇ ਸਿੰਗਲ ਕਿਉਬਿੱਟ ਉੱਤੇ ਕ੍ਰਿਆ ਕਰਦਾ ਹੈ। ਇਹ ਮੁਢਲੀ ਅਵਸਥਾ ਨੂੰ ਅਤੇ to ਨੂੰ ਮੇਲਦਾ ਹੈ, ਜਿਸਦਾ ਅਰਥ ਹੈ ਕਿ ਕਿਸੇ ਨਾਪ ਦਾ 1 ਜਾਂ 0 ਹੋ ਜਾਣ ਦੀ ਇੱਕ ਬਰਾਬਰ ਪ੍ਰੋਬੇਬਿਲਿਟੀ ਹੁੰਦੀ ਹੈ (ਯਾਨਿ ਕਿ, ਇੱਕ ਸੁਪਰਪੁਜੀਸ਼ਨ ਰਚਦਾ ਹੈ)। ਇਹ ਬਲੋਚ ਸਫੀਅਰ ਉੱਤੇ ਧੁਰੇ ਦੁਆਲੇ ਦੀ ਇੱਕ ਰੋਟੇਸ਼ਨ ਪ੍ਰਸਤੁਤ ਕਰਦਾ ਹੈ। ਸਪਸ਼ਟ ਹੈ ਕਿ, ਇਹ ਦੋ ਰੇਟੇਸ਼ਨਾਂ, Z-ਧੁਰੇ ਦੁਆਲੇ ਰੋਟੇਸ਼ਨ, ਅਤੇ ਇਸ ਤੋਂ ਬਾਦ Y-ਧੁਰੇ ਦੁਆਲੇ ਰੋਟੇਸ਼ਨ ਦਾ ਮੇਲ ਹੁੰਦਾ ਹੈ। ਇਹ ਹਦਮਰਦ ਮੈਟ੍ਰਿਕਸ ਦੁਆਰਾ ਪ੍ਰਸਤੁਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ।

- .
ਹਦਮਰਦ ਗੇਟ ਕੁਆਂਟਮ ਫੋਰੀਅਰ ਟ੍ਰਾਂਸਫੋਰਮ ਦਾ ਇੱਕ ਕਿਉਬਿੱਟ ਰੂਪ ਹੁੰਦਾ ਹੈ। ਕਿਉਂਕਿ ਹੁੰਦਾ ਹੈ ਜਿੱਥੇ; I ਆਇਡੈਂਟਿਟੀ ਮੈਟ੍ਰਿਕਸ ਹੁੰਦਾ ਹੈ, H (ਹੋਰ ਕੁਆਂਟਮ ਲੌਜੀਕਲ ਗੇਟਾਂ ਵਾਂਗ) ਇੱਕ ਯੁਨਾਇਟ੍ਰੀ ਮੈਟ੍ਰਿਕਸ ਹੁੰਦਾ ਹੈ। ਇਸਦੇ ਨਾਲ ਹੀ, .
ਪੌਲੀ-X ਗੇਟ
[ਸੋਧੋ]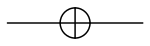
ਪੌਲੀ-X ਕਿਸੇ ਸਿੰਗਲ ਕਿਉਬਿੱਟ ਉੱਤੇ ਕ੍ਰਿਆ ਕਰਦਾ ਹੈ। ਇਹ ਕਲਾਸੀਕਲ ਕੰਪਿਊਟਰਾ਼ ਲਈ NOT ਗੇਟ ਦਾ ਕੁਆਂਟਮ ਬਦਲ ਹੈ। (ਮਿਆਰੀ ਅਧਾਰ , ਦੇ ਸੰਦ੍ਰਭ ਵਿੱਚ, ਜੋ Z-ਦਿਸ਼ਾ ਨੂੰ ਇਸ ਸਮਝ ਮੁਤਾਬਿਕ ਵੱਖਰਾ ਕਰਦਾ ਹੈ ਕਿ; ਆਈਗਨਮੁੱਲ +1 ਦਾ ਇੱਕ ਨਾਪ, ਕਲਾਸੀਕਲ 1/ਸੱਚ ਨਾਲ ਸਬੰਧ ਰੱਖਦਾ ਹੈ ਅਤੇ -1 ਦਾ ਸਬੰਧ 0/ਝੂਠ) ਨਾਲ ਹੁੰਦਾ ਹੈ।
ਇਹ ਬਲੋਚ ਸਫੀਅਰ ਦੇ X-ਧੁਰੇ ਦੁਆਲੇ ਰੇਡੀਅਨ ਦੇ ਇੱਕ ਘੁਮਾਵ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ। ਇਹ ਨੂੰ ਤੱਕ ਅਤੇ ਨੂੰ ਤੱਕ ਮੈਪ ਕਰਦਾ ਹੈ। ਇਸ ਫਿਤਰਤ ਕਾਰਨ, ਇਸਨੂੰ ਕਦੇ ਕਦੇ ਬਿੱਟ-ਫਲਿਪ Archived 2019-02-16 at the Wayback Machine. ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇਸਨੂੰ ਪੌਲੀ X ਮੈਟ੍ਰਿਕਸ ਰਾਹੀਂ ਪੇਸ਼ ਕੀਤਾ ਜਾਂਦਾ ਹੈ:
- .
ਪੌਲੀ-Y ਗੇਟ
[ਸੋਧੋ]ਪੌਲੀ-Y ਗੇਟ ਕਿਸੇ ਸਿੰਗਲ ਕਿਉਬਿਟ ਉੱਤੇ ਕ੍ਰਿਆ ਕਰਦਾ ਹੈ। ਇਹ ਬਲੋਚ ਸਫੀਅਰ ਦੇ Y -ਧੁਰੇ ਦੁਆਲੇ ਰੇਡੀਅਨ ਦੇ ਇੱਕ ਘੁਮਾਵ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ। ਇਹ ਨੂੰ ਤੱਕ ਅਤੇ ਨੂੰ ਤੱਕ ਮੈਪ ਕਰਦਾ ਹੈ। ਇਸਨੂੰ ਪੌਲੀ Y ਮੈਟ੍ਰਿਕਸ ਰਾਹੀਂ ਪੇਸ਼ ਕੀਤਾ ਜਾਂਦਾ ਹੈ:
- .
ਪੌਲੀ-Z () ਗੇਟ
[ਸੋਧੋ]ਪੌਲੀ- Z ਗੇਟ ਕਿਸੇ ਸਿੰਗਲ ਕਿਉਬਿਟ ਉੱਤੇ ਕ੍ਰਿਆ ਕਰਦਾ ਹੈ। ਇਹ ਬਲੋਚ ਸਫੀਅਰ ਦੇ Z -ਧੁਰੇ ਦੁਆਲੇ ਰੇਡੀਅਨ ਦੇ ਇੱਕ ਘੁਮਾਵ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ। ਇਸ ਕਰਕੇ ਇਹ ਵਾਲਾ ਕਿਸੇ ਫੇਜ਼ ਸ਼ਿਫਟ ਗੇਟ ਦਾ ਇੱਕ ਖਾਸ ਮਾਮਲਾ ਹੁੰਦਾ ਹੈ (ਜੋ ਅਗਲੇ ਉੱਪ-ਹਿੱਸ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ)।. ਇਹ ਅਧਾਰ ਅਵਸਥਾ ਨੂੰ ਬਗੈਰ ਬਦਲੇ ਛੱਡ ਦਿੰਦਾ ਹੈ ਅਤੇ ਨੂੰ ਤੱਕ ਮੈਪ ਕਰਦਾ ਹੈ। ਇਸ ਫਿਤਰਤ ਕਾਰਨ ਇਸਨੂੰ ਕਦੇ ਕਦੇ ਫੇਜ਼-ਫਲਿਪ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇਸਨੂੰ ਪੌਲੀ Z ਮੈਟ੍ਰਿਕਸ ਰਾਹੀਂ ਪੇਸ਼ ਕੀਤਾ ਜਾਂਦਾ ਹੈ:
- .
ਪੌਲੀ ਮੈਟ੍ਰਿਕਸ ਇਨਵਲਟਰੀ ਹੁੰਦੇ ਹਨ
[ਸੋਧੋ]ਕਿਸੇ ਪੌਲੀ ਮੈਟ੍ਰਿਕਸ ਦਾ ਸਕੁਏਅਰ, ਆਇਡੈਂਟਿਟੀ ਮੈਟ੍ਰਿਕਸ ਹੁੰਦਾ ਹੈ।
NOT ਗੇਟ ਦਾ ਵਰਗਮੂਲ (√NOT)
[ਸੋਧੋ]
NOT ਗੇਟ ਦਾ ਵਰਗਮੂਲ (ਜਾਂ ਪੌਲੀ-X, ਦਾ ਵਰਗਮੂਲ) ਕਿਸੇ ਸਿੰਗਲ ਕਿਉਬਿਟ ਉੱਤੇ ਕ੍ਰਿਆ ਕਰਦਾ ਹੈ। ਇਹ ਅਧਾਰ ਅਵਸਥਾ ਨੂੰ ਤੱਕ ਅਤੇ ਨੂੰ ਤੱਕ ਮੈਪ ਕਰਦਾ ਹੈ।
- .
ਇਸਲਈ, ਹੁੰਦਾ ਹੈ। ਇਸਲਈ ਇਹ ਗੇਟ NOT ਗੇਟ ਦਾ ਵਰਗਮੂਲ ਹੁੰਦਾ ਹੈ।
ਵਰਗਮੂਲ ਗੇਟਾਂ ਨੂੰ ਸਾਰੇ ਹੋਰ ਗੇਟਾਂ ਲਈ ਰਚਿਆ ਜਾ ਸਕਦਾ ਹੈ ਬਸ਼ਰਤੇ ਇੱਕ ਅਜਿਹਾ ਯੂਨਾਇਟ੍ਰੀ ਮੈਟ੍ਰਿਕਸ ਖੋਜਿਆ ਜਾਵੇ, ਜਿਸ ਨੂੰ ਓਸੇ ਨਾਲ ਗੁਣਾ ਕਰਨ ਤੇ, ਉਹ ਗੇਟ ਪੈਦਾ ਹੋ ਜਾਵੇ, ਜਿਸਦਾ ਵਰਗਮੂਲ ਗੇਟ ਰਚਣਾ ਹੋਵੇ। ਸਾਰੇ ਗੇਟਾਂ ਦੇ ਸਾਰੇ ਰੇਸ਼ਨਲ ਐਕਸਪੋਨੈਂਟ ਇਸੇ ਤਰਾਂ ਖੋਜੇ ਜਾ ਸਕਦੇ ਹਨ।
ਇਹ ਵੀ ਦੇਖੋ
[ਸੋਧੋ]- ਏਡੀਆਬੈਟਿਕ ਕੁਆਂਟਮ ਕੰਪਿਊਟੇਸ਼ਨ
- ਲਾਂਦਾਓਰ ਦਾ ਸਿਧਾਂਤ
- ਪੌਲੀ ਮੈਟ੍ਰਿਕਸ
- ਕੁਆਂਟਮ ਅਲੌਹਰਿਥਮ
- ਕੁਆਂਟਮ ਸਰਕਟ
- ਕੁਆਂਟਮ ਨੈਟਵਰਕ
- ਕੁਆਂਟਮ ਮੈਮਰੀ
- ਕੁਆਂਟਮ ਅਵਸਥਾ
ਹਵਾਲੇ
[ਸੋਧੋ]- ↑ Phys. Rev. A 52 3457–3467 (1995), doi:10.1103/PhysRevA.52.3457; e-print arXiv:quant-ph/9503016/{{{2}}}
- ↑ R. P. Feynman, "Quantum mechanical computers", Optics News, February 1985, 11, p. 11; reprinted in Foundations of Physics 16(6) 507–531.
ਸੋਮੇ
[ਸੋਧੋ]- Nielsen, Michael A.; Chuang, Isaac (2000). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press. ISBN 0521632358. OCLC 43641333.
- ਫਰਮੇ ਦੀ ਵਰਤੋਂ ਵਿੱਚ ਦੁਹਰਾਇਆ ਕੁੰਜੀਆਂ
- Use American English from April 2019
- All Wikipedia articles written in American English
- Articles with hatnote templates targeting a nonexistent page
- Articles needing additional references from February 2018
- Articles with invalid date parameter in template
- All articles needing additional references
- ਕੁਆਂਟਮ ਗੇਟ
- ਕੁਆਂਟਮ ਸੂਚਨਾ ਵਿਗਿਆਨ
- ਲੌਜਿਕ ਗੇਟ


































