ਸਟਰਿੰਗ ਥਿਊਰੀ
| ਸਟਰਿੰਗ ਥਿਊਰੀ |
|---|
 |
| ਮੁਢਲੀਆਂ ਵਸਤੂਆਂ |
| ਪਰਚਰਬੇਟਿਚ ਥਿਊਰੀ |
| ਗੈਰ-ਪਰਚਰਬੇਟਿਵ ਨਤੀਜੇ |
| ਫੀਨੋਮੀਨੌਲੌਜੀ |
| ਗਣਿਤ |
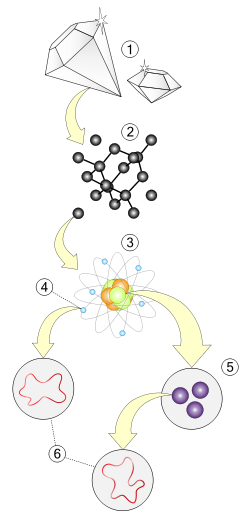
੧. ਵੱਡਾ ਪੱਧਰ: ਮਾਦਾ
੨. ਅਣੂ ਪੱਧਰ
੩. ਪਰਮਾਣੂ ਪੱਧਰ: ਪ੍ਰੋਟਾਨ, ਨਿਊਟਰਾਨ ਅਤੇ ਇਲੈਕਟਰਾਨ
੪. ਉੱਪ-ਪਰਮਾਣੂ ਪੱਧਰ: ਇਲੈਕਟਰਾਨ
੫. ਉੱਪ-ਪਰਮਾਣੂ ਪੱਧਰ: ਕੁਆਰਕ
੬. ਡੋਰ-ਪੱਧਰ
ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ, ਸਟਰਿੰਗ ਥਿਊਰੀ (ਜਾਂ ਡੋਰੀ ਸਿਧਾਂਤ) ਇੱਕ ਸਿਧਾਂਤਕ ਢਾਂਚਾ ਹੈ ਜਿਸ ਵਿੱਚ ਪਾਰਟੀਕਲ ਫ਼ਿਜ਼ਿਕਸ ਦੇ ਬਿੰਦੂ ਵਰਗੇ ਕਣਾਂ ਨੂੰ 1-ਪਸਾਰੀ ਵਸਤੂਆਂ ਵਿੱਚ ਬਦਲ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਜਿਹਨਾਂ ਨੂੰ ਸਟਰਿੰਗ (ਡੋਰੀਆਂ) ਕਹਿੰਦੇ ਹਨ। ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ, ਦੇਖੇ ਗਏ ਮੁੱਢਲੇ ਕਣਾਂ ਦੀਆਂ ਵੱਖਰੀਆਂ ਕਿਸਮਾਂ ਇਹਨਾਂ ਸਟਰਿੰਗਾਂ ਦੀਆਂ ਵੱਖਰੀਆਂ ਵੱਖਰੀਆਂ ‘ਕੁਆਂਟਮ ਹਾਲਤਾਂ’ ਤੋਂ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ। ਪਾਰਟੀਕਲ ਫਿਜਿਕਸ ਦੇ ਸਟੈਂਡਰਡ ਮਾਡਲ ਵਿੱਚ ਦਿਖਾਏ ਕਣਾਂ ਤੋਂ ਇਲਾਵਾ, ਸਟਰਿੰਗ ਥਿਊਰੀ ਕੁਦਰਤੀ ਤੌਰ ਤੇ ਗੁਰੂਤਾ ਖਿੱਚ ਨਾਲ ਵੀ ਮੇਲ ਖਾਂਦੀ ਹੈ, ਜਿਸ ਕਾਰਨ ਹਰੇਕ ਚੀਜ਼ ਦੀ ਥਿਊਰੀ ਦੇ ਯੋਗ ਹੈ, ਜੋ ਸਾਰੇ ਮੁੱਢਲੇ ਕਣ ਅਤੇ ਪਦਾਰਥ ਦੀਆਂ ਕਿਸਮਾਂ ਨੂੰ ਦਰਸਾਉਣ ਵਾਲਾ ਇੱਕ ਆਤਮ-ਨਿਰਭਰ ਗਣਿਤਿਕ ਮਾਡਲ ਹੈ। ਕਣ ਭੌਤਿਕੀ ਵਿੱਚ ਇਸ ਧਾਰਨਾ ਦੇ ਰੋਲ ਤੋਂ ਇਲਾਵਾ, ਸਟਰਿੰਗ ਥਿਊਰੀ ਹੁਣ ਵੱਡੇ ਪੱਧਰ ਤੇ ਇੱਕ ਸਿਧਾਂਤਕ-ਸ਼ਾਸਤਰ ਦੇ ਰੂਪ ਵਿੱਚ ਵਰਤੀ ਜਾਂਦੀ ਹੈ, ਤੇ ਇਸਨੇ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਤੇ ਕੁਆਂਟਮ ਗਰੈਵਟੀ ਦੇ ਬਹੁਤ ਸਾਰੇ ਪਹਿਲੂਆਂ ਤੇ ਰੌਸ਼ਨੀ ਪਾਈ ਹੈ।
ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੇ ਸਭ ਤੋਂ ਪਹਿਲੇ ਮਾਡਲ ਵਿੱਚ, ਜਿਸ ਨੂੰ ਬੋਸੋਨਿਕ ਸਟਰਿੰਗ ਥਿਊਰੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਸਿਰਫ ਬੋਸੋਨ ਕਣਾਂ ਦੀ ਸ਼੍ਰੇਣੀ ਦਾ ਸਹਿਯੋਗ ਕੀਤਾ ਗਿਆ, ਬੇਸ਼ਕ ਇਹ ਥਿਊਰੀ ਬਾਦ ਵਿੱਚ ਸੁਪਰਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ ਵਿਕਸਿਤ ਹੋ ਗਈ, ਜਿਸਨੇ ਦਰਸਾਇਆ ਕਿ ਬੋਸੋਨ ਅਤੇ ਫਰਮੀਔਨ ਕਣਾਂ ਦਰਮਿਆਨ ਇੱਕ ਸੁਪਰਸਮਰੂਪਤਾ (supersymmetry) ਦਾ ਸਬੰਧ ਹੈ। ਸਟਰਿੰਗ ਥਿਊਰੀ ਨੂੰ ਵਾਧੂ ਸਥਾਨਿਕ ਅਯਾਮਾਂ ਦੀ ਜਰੂਰਤ ਪੈਂਦੀ ਹੈ ਤਾਂ ਜੋ ਇਸਦਾ ਗਣਿਤ ਸਥਿਰ ਰਹੇ| ਸਟਰਿੰਗ ਥਿਊਰੀ ਤੋਂ ਬਣੇ ਵਾਸਤਵਿਕ ਭੌਤਿਕੀ ਮਾਡਲ ਵਿੱਚ, ਇਹ ਵਾਧੂ ਅਯਾਮ ਬਹੁਤ ਸੂਖਮਤਾ ਦੇ ਦਰਜੇ ਤੱਕ ਸੁੰਗੜੇ (compactified) ਹੁੰਦੇ ਹਨ।
ਸਟਰਿੰਗ ਥਿਊਰੀ ਸਭ ਤੋਂ ਪਹਿਲੀ ਵਾਰ 1960ਵੇਂ ਦਹਾਕੇ ਦੇ ਅਖੀਰ ਵਿੱਚ ਤਾਕਤਵਰ ਕੇਂਦਰੀ ਬਲ ਦੀ ਥਿਊਰੀ ਦੇ ਰੂਪ ਵਿੱਚ ਪੜੀ ਗਈ ਜਿਸਤੋਂ ਬਾਦ ਕੁਆਂਟਮ ਕਰੋਮੋਡਇਨੈਮਿਕਸ ਥਿਊਰੀ ਦੇ ਪੱਖ ਵਿੱਚ ਛੱਡ ਦਿੱਤੀ ਗਈ| ਫਲਸਰੂਪ, ਇਹ ਮਹਿਸੂਸ ਕੀਤਾ ਗਿਆ ਕਿ ਸਟ੍ਰਿੰਗ ਥਿਊਰੀ ਦੀਆਂ ਮੁਢਲੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਜੋ ਪ੍ਰਮਾਣੂ ਭੌਤਿਕੀ ਥਿਊਰੀ ਲਈ ਯੋਗ ਨਹੀਂ ਸਨ ਉਹ ਕੁਆਂਟਮ ਗਰੂਤਾਕਰਸ਼ਨ ਥਿਊਰੀ ਦੇ ਯੋਗ ਹਨ। 1990ਵੇਂ ਦਹਾਕੇ ਦੇ ਮੱਧ ਵਿੱਚ ਰਿਲੀਜ਼ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੇ 5 ਸਥਿਰ ਰੂਪ ਵਿਕਸਤ ਕੀਤੇ ਗਏ ਕਿ ਇਹ 5 ਥਿਊਰੀਆਂ ਜੋੜ ਕੇ ਇੱਕ ਵੱਖਰੀ 11-ਅਯਾਮੀ M-ਥਿਊਰੀ ਬਣੀ ਜਿਸਦੀਆਂ ਵੱਖਰੀਆਂ ਵੱਖਰੀਆਂ ਸੀਮਾਵਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਇਹ 5 ਕਿਸਮਾਂ ਬਣ ਸਕਦੀਆਂ ਸਨ।
ਬਹੁਤ ਸਾਰੇ ਭੌਤਕ ਸ਼ਾਸਤਰੀ (ਜਿਵੇਂ, ਸਟੀਫਨ ਹਾਕਿੰਗ, ਐਡਵਰਡ ਵਿੱਟਨ, ਅਤੇ ਜੁਆਨ ਮਾਲਡਸੀਨਾ) ਮੰਨਦੇ ਹਨ ਕਿ ਸਟਰਿੰਗ ਥਿਊਰੀ ਕੁਦਰਤ ਦੇ ਮੁਢਲੇ ਵਿਸਥਾਰ ਨੂੰ ਸਹੀ ਕਰਨ ਵੱਲ ਕਦਮ ਹੈ। ਅਜਿਹਾ ਇਸ ਲਈ ਹੈ ਕਿਉਂਕਿ ਇਹ ਥਿਊਰੀ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਅਤੇ ਜਨਰਲ ਰਿਲੇਟਿਵਿਟੀ ਦੇ ਸਥਾਈ ਮੇਲ ਨੂੰ ਸੰਭਵ ਕਰਦੀ ਹੈ, ਕੁਆਂਟਮ ਗਰੈਵਿਟੀ ਦੀਆਂ ਆਮ ਗਹਿਰਾਈਆਂ ਜਿਵੇਂ ਹੋਲੋਗਰਾਫਿਕ ਸਿਧਾਂਤ ਤੇ ਬਲੈਕ ਹੋਲ ਥਰਮੋਡਾਇਨਾਮਿਕਸ ਨਾਲ ਵੀ ਸਹਿਮਤ ਹੈ, ਅਤੇ ਇਸਨੇ ਬਹੁਤ ਸਾਰੇ ਅੰਦਰੂਨੀ ਸਥਿਰਤਾ ਦੇ ਗੰਭੀਰ ਟੈਸਟ ਪਾਸ ਕੀਤੇ ਹਨ। ਖਾਸ ਕਰ ਕੇ ਸਟੀਫਨ ਹਾਕਿੰਗ ਮੁਤਾਬਕ, ‘M- ਥਿਊਰੀ ਹੀ ਬ੍ਰਹਿਮੰਡ ਦੀ ਸੰਪੂਰਨ ਥਿਊਰੀ ਦੇ ਕਾਬਲ ਹੈ।” ਹੋਰ ਭੌਤਿਕ ਵਿਗਿਆਨੀ , ਜਿਵੇਂ ਰਿਚਰਡ ਫੇਨਮੇਨ, ਰੋਜਰ ਪੈਨਰੋਸ, ਸ਼ੇਲਡਨ ਲੀ ਗਲਾਸ਼ੋ, ਨੇ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੀ ਅਲੋਚਨਾ ਕੀਤੀ ਹੈ ਕਿਉਂਕਿ ਇਹ ਊਰਜਾ ਦੇ ਪੈਮਾਨਿਆਂ ਤੇ ਪ੍ਰਯੋਗਾਂ ਦੀ ਭਵਿੱਖਬਾਣੀ ਦੀ ਕਥਾ ਨਹੀਂ ਉਪਲਬਧ ਕਰਵਾਉਂਦੀ ਅਤੇ ਤੇ ਕਿਹਾ ਕਿ ਇਹ ਹਰੇਕ ਚੀਜ਼ ਦੀ ਥਿਊਰੀ ਦੇ ਤੌਰ ਤੇ ਅਸਫਲ ਹੈ।
ਸਟਰਿੰਗ ਥਿਊਰੀ ਤੱਤ-ਨਿਖੇੜ
[ਸੋਧੋ]
ਸਟਰਿੰਗ ਥਿਊਰੀ ਦਾ ਸ਼ੁਰੂਆਤੀ ਵਿਚਾਰ ਇਹ ਹੈ ਹੈ ਕਿ ਪਾਰਟੀਕਲ ਫਿਜਿਕਸ ਦੇ ਬਿੰਦੂ ਵਰਗੇ ਕਣਾਂ ਨੂੰ ਸਟਰਿੰਗ ਨਾਮਕ 1-ਅਯਾਮੀ ਵਸਤੂਆਂ ਵਿੱਚ ਪੇਸ਼ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਸਟਰਿੰਗ ਥਿਊਰੀ ਮੁਤਾਬਿਕ, ਸਟਰਿੰਗ ਕਈ ਤਰੀਕਿਆਂ ਨਾਲ ਕੰਪਨ ਕਰ ਸਕਦੇ ਹਨ। ਸਟਰਿੰਦਾਂ ਦੇ ਅਰਧ ਵਿਆਸ ਤੋਂ ਵੱਧ ਵਾਲੇ ਸਥਾਨਾਂ ਤੇ , ਹਰੇਕ ਕੰਪਨ ਦਾ ਤਰੀਕਾ ਵੱਖਰੇ ਕਿਸਮ ਦੇ ਪੂੰਜ, ਚਾਰਜ ਅਤੇ ਹੋਰ ਗੁਣਾਂ ਵਾਲੇ ਦੇ ਕਣ ਨੂੰ ਰਚਦਾ ਹੈ ਜੋ ਸਟਰਿੰਗ ਡਾਇਨੈਮਿਕਸ ਨਾਲ ਨਾਪੇ ਜਾ ਸਕਦੇ ਹਨ। ਸਟਰਿੰਗਾਂ ਦਾ ਟੁੱਟਣਾ ਤੇ ਦੁਬਾਰਾ ਜੁੜਨਾ ਕਣਾਂ ਦੇ ਪੈਦਾ ਹੋਣ ਤੇ ਗ੍ਰਹਿਣ ਕੀਤੇ ਜਾਣ ਨਾਲ ਸਬੰਧ ਰੱਖਦਾ ਹੈ, ਜੋ ਕਣਾਂ ਵਿਚਕਾਰਲੀ ਪਰਸਪਰ ਕ੍ਰਿਆਵਾਂ ਨੂੰ ਪੈਦਾ ਕਰਦੀ ਹੈ। ਸਟਰਿੰਗਾਂ ਦੇ ਕੰਪਨ ਦੇ ਤਰੀਕਿਆਂ ਦੀ ਉਦਾਹਰਨ ਇੱਕ ਗਿਟਾਰ ਦੀ ਤਾਰ ਦੁਆਰਾ ਪੈਦਾ ਹੋਣ ਵਾਲੀਆਂ ਕਈ ਵੱਖਰੀਆਂ ਸੰਗੀਤ ਦੀਆਂ ਧੁਨਾਂ ਵਾਂਗ ਹੈ। ਇਸ ਉਦਾਹਰਨ ਵਿੱਚ, ਵੱਖਰੀਆਂ ਧੁਨਾਂ ਵੱਖਰੇ ਕਣਾਂ ਨਾਲ ਸਬੰਧਤ ਹਨ।
ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ, ਸਟਰਿੰਗ ਦੇ ਕੰਪਨ ਦੇ ਤਰੀਕਿਆਂ ਵਿੱਚੋਂ ਇੱਕ ਤਰੀਕੇ ਦਾ ਸਬੰਧ ਇੱਕ ਪੁੰਜਹੀਣ, ਸਪਿਨ-2 ਕਣ ਨਾਲ ਹੈ। ਅਜਿਹਾ ਕਣ ਗਰੈਵੀਟੋਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਹ ਅਜਿਹੇ ਬਲ ਨੂੰ ਸਵਾਰੀ ਕਰਾਉਂਦਾ ਹੈ ਜਿਸ ਵਿੱਚ ਗਰੂਤਾਕਰਸ਼ਨ ਦਾ ਗੁਣ ਹੁੰਦਾ ਹੈ। ਕਿਉਂਕਿ ਸਟਰਿੰਗ ਥਿਊਰੀ ਨੂੰ ਇੱਕ ਸਥਿਰ ਗਣਿਤਕ ਕੁਆਂਟਮ ਮਕੈਨਿਕਸ ਥਿਊਰੀ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ, ਇਸਲਈ ਇਸ ਗਰੈਵੀਟੋਨ ਕਣ ਦੀ ਹੋਂਦ ਦੀ ਅਵਸਥਾ ਦਾ ਮਤਲਬ ਹੈ ਕਿ ਸਟਰਿੰਗ ਥਿਊਰੀ ਕੁਆਂਟਮ ਗਰੈਵਟੀ ਦੀ ਥਿਊਰੀ ਹੈ।
ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ ਦੋਹੇ ਤਰਾਂ ਦੇ ਸਟਰਿੰਗ ਸ਼ਾਮਿਲ ਹਨ। ਜਿਹਨਾਂ ਵਿੱਚ ਇੱਕ ਖੁੱਲੇ ਸਟਰਿੰਗ ਹੁੰਦੇ ਹਨ ਜਿਹਨਾਂ ਦੇ ਦੋ ਵੱਖਰੇ ਅੰਤਿਮਬਿੰਦੂ (ਸਿਰੇ) ਹੁੰਦੇ ਹਨ। ਦੂਜੀ ਤਰਾਂ ਦੇ ਸਟਰਿੰਗ ਪੂਰਾ ਚੱਕਰ ਬਣਾਉਂਦੇ ਹਨ, ਯਾਨਿ ਕਿ ਬੰਦ ਸਿਰਿਆਂ ਵਾਲੇ ਹੁੰਦੇ ਹਨ। ਦੋਵੇਂ ਕਿਸਮ ਦੇ ਸਟਰਿੰਗ ਜਰਾ ਵੱਖਰੇ ਤਰੀਕੇ ਨਾਲ ਵਰਤਾਓ ਕਰਦੇ ਹਨ, ਤੇ ਵੱਖਰੀ ਕਿਸਮ ਦੇ ਕਣ ਰਚਦੇ ਹਨ। ਜਿਵੇਂ, ਸਾਰੀਆਂ ਸਟਰਿੰਗ ਥਿਊਰੀਆਂ ਵਿੱਚ ਬੰਦ ਸਟਰਿੰਗ ਗਰੈਵੀਟੋਨ ਤਰੀਕੇ ਹਨ, ਪਰ ਸਿਰਫ ਖੁੱਲੇ ਸਿਰਿਆਂ ਵਾਲੇ ਸਟਰਿੰਗ ਹੀ ਫੋਟੋਨ ਨਾਮਕ ਕਣਾਂ ਨਾਲ ਸਬੰਧ ਰੱਖਦੇ ਹਨ। ਕਿਉਂਕਿ ਇੱਕ ਖੁੱਲੇ ਸਟਰਿੰਗ ਦੇ ਦੋਹੇ ਸਿਰੇ ਹਮੇਸ਼ਾ ਮੁਲ ਕੇ ਜੁੜ ਸਕਦੇ ਹਨ. ਤੇ ਬੰਦ ਸਟਰਿੰਗ ਰਚ ਸਕਦੇ ਹਨ, ਇਸਲਈ ਸਾਰੀਆਂ ਥਿਊਰੀਆਂ ਵਿੱਚ ਬੰਦ ਸਟਰਿੰਗ ਹੁੰਦੇ ਹਨ। ਇੱਕ ਸਟਰਿੰਗ ਦੀ ਲੰਬਾਈ ਪਲੈਂਕ ਲੰਬਾਈ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ। ਸ਼ੁਰੂਆਤੀ ਮਾਡਲ ਵਿੱਚ, ਬੋਸੋਨਿਕ ਸਟਰਿੰਗ, ਨੇ ਸਿਰਫ ਬੋਸੋਨ ਕਣਾਂ ਦੀ ਸ਼੍ਰੇਣੀ ਦਾ ਹੀ ਸਹੋਯੋਗ ਕੀਤਾ| ਇਹ ਮਾਡਲ, ਘੱਟ ਊਰਜਾਵਾਂ ਤੇ, ਇੱਕ ਕੁਆਂਟਮ ਗਰੈਵਟੀ ਥਿਊਰੀ, ਜਿਸ ਵਿੱਚ ਗੇਜ਼ ਬੋਸੋਨ ਜਿਵੇਂ ਫੋਟੌਨ ਵੀ ਸ਼ਾਮਿਲ ਹਨ (ਜੇਕਰ ਖੁੱਲੇ ਸਿਰੇ ਵਾਲੇ ਸਟਰਿੰਗ ਵੀ ਸ਼ਾਮਲ ਕਰ ਲਏ ਜਾਣ) ਦੀ ਵਿਆਖਿਆ ਕਰਦਾ ਹੈ। ਫੇਰ ਵੀ, ਇਸ ਮਾਡਲ ਵਿੱਚ ਸਮੱਸਿਆਵਾਂ ਹਨ। ਸਭ ਤੋਂ ਜਿਆਦਾ ਮਹੱਤਵਪੂਰਨ ਇਹ ਹੈ ਕਿ ਥਿਊਰੀ ਵਿੱਚ ਮੂਲ ਅਥਿਰਤਾ ਹੁੰਦੀ ਹੈ, ਜੋ ਨਤੀਜੇ ਵਜੋਂ ਅਪਣੇ ਆਪ ਵਿੱਚ ਹੀ ਸਪੇਸ ਸਮੇਂ ਦਾ ਰਿਸਾਓ ਕਰਦਾ ਮੰਨੀ ਜਾਂਦੀ ਹੈ(ਘੱਟੋ ਘੱਟ ਅੰਸ਼ਿਕ ਰੂਪ ਵਿੱਚ)| ਇਸਦੇ ਨਾਲ ਹੀ, ਜਿਵੇਂ ਇਸਦਾ ਨਾਮ ਦਰਸਾਉਂਦਾ ਹੈ ਕਣਾਂ ਦਾ ਰੰਗ-ਪੱਟਾ (ਸਪੈਕਟਰਮ) ਸਿਰਫ ਬੋਸਨਾਂ ਦਾ ਹੀ ਹੈ ਅਤੇ ਕਣ ਜਿਵੇਂ ਫੋਟੀਨ , ਵਤੀਰੇ ਦੇ ਖਾਸ ਗੁਣਾਂ ਦੀ ਪਾਲਣਾ ਕਦੇ ਹਨ, ਦਾ ਹੈ। ਮੋਟੇ ਤੌਰ ਤੇ ਕਹਿੰਦੇ ਹੋਏ, ਬੋਸਨ ਰਿਸਾਓ ਦੇ ਜਨਮਦਾਤਾ ਕਣ ਹਨ, ਪਰ ਪਦਾਰਥ ਦੇ ਨਹੀਂ, ਜੋ ਫਰਮੀਔਨਜ਼ ਦਾ ਬਣਿਆ ਹੁੰਦਾ ਹੈ।ਇਹ ਜਾਂਚ ਕਰਦੇ ਹੋਏ ਕਿ ਕਿਵੇਂ ਸਟਰਿੰਗ ਥਿਊਰੀ ਫਰਮੀਔਨ ਵੀ ਸ਼ਾਮਲ ਕਰ ਸਕਦੀ ਹੈ ਨੇ ਸੁਪਰਸਮਿਟਰੀ ਦੀ ਖੋਜ ਨੂੰ ਜਨਮ ਦਿੱਤਾ, ਜੋ ਬੋਸੌਨਾਂ ਅਤੇ ਫਰਮੀਔਨਾਂ ਦਰਮਿਆਨ ਗਣਿਤਿਕ ਸਬੰਧ ਹੈ। ਫਰਮਿਔਨ ਕੰਪਨਾ ਸਮੇਤ ਵਾਲੀ ਥਿਊਰੀਆਂ ਨੂੰ ਸੁਪਰਸਟਰਿੰਗ ਥਿਊਰੀਆਂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ; ਕਈ ਕਿਸਮਾਂ ਦਰਸਾਈਆਂ ਗਈਆਂ ਹਨ, ਪਰ ਹੁਣ ਸਾਰੀਆ M-ਥਿਊਰੀ ਦੀਆਂ ਵੱਖਰੀਆਂ ਸੀਮਾਵਾਂ ਹੋਣ ਦੇ ਰੂਪ ਵਿੱਚ ਸੋਚੀਆਂ ਜਾਂਦੀਆਂ ਹਨ।
ਕਿਉਂਕਿ ਸਟਰਿੰਗ ਥਿਊਰੀ ਸਾਰੀਆਂ ਮੁਢਲੀਆਂ ਕਿਰਿਆਵਾਂ ਨਾਲ ਮੇਲ ਖਾਂਦੀ ਹੈ, ਜਿਸ ਵਿੱਚ ਗਰੈਵਟੀ ਵੀ ਸ਼ਾਮਲ ਹੈ, ਕਈ ਵਿਗਿਆਨੀਆਂ ਨੂੰ ਉਮੀਦ ਹੈ ਕਿ ਇਹ ਸਾਡੇ ਬ੍ਰਹਿਮੰਡ ਨੂੰ ਪੂਰੀ ਤਰਾਂ ਦਰਸਾਉਂਦੀ ਹੈ ਤੇ ਇਸ ਨੂੰ ਥਿਊਰੀ ਆਫ ਐਵਰੀਥਿੰਗ ਬਣਾ ਦਿੰਦੀ ਹੈ। ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ ਤਾਜਾ ਖੋਜਾਂ ਦਾ ਇੱਕ ਮੁੱਖ ਮੰਤਵ ਅਜਿਹੀ ਥਿਊਰੀ ਦਾ ਹੱਲ ਲੱਭਣਾ ਹੈ ਜੋ ਸਟੈਂਡਰਡ ਮਾਡਲ ਨਾਲ ਨਤੀਜਿਆਂ ਦੇ ਰੂਪ ਵਿੱਚ ਮੇਲ ਖਾਵੇ, ਛੋਟੇ ਬ੍ਰਹਿਮੰਡੀ ਸਥਿਰ ਅੰਕ ਨਾਲ ਮੇਲ ਖਾਵੇ, ਜਿਸ ਵਿੱਚ ਡਾਰਕ ਮੈਟਰ ਹੁੰਦਾ ਹੈ ਤੇ ਬ੍ਰਹਿਮੰਡੀ ਮੁਦਰਾਸਫੀਰਤੀ (cosmic inflation) ਲਈ ਤਰੀਫ ਦੇ ਕਾਬਲ ਤੰਤਰ ਨਾਲ ਮੇਲ ਖਾਵੇ| ਇਹ ਅਜੇ ਤੱਕ ਅਗਿਆਤ ਹੈ ਕਿ ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ ਕੋਈ ਅਜਿਹਾ ਹੱਲ ਹੈ, ਨਾ ਇਹ ਪਤਾ ਚੱਲਿਆ ਹੈ ਕਿ ਇਹ ਥਿਊਰੀ ਵਿਸਥਾਰ ਦੀ ਚੋਣ ਲਈ ਕਿੰਨੀ ਕੁ ਅਜਾਦੀ ਦੀ ਆਗਿਆ ਦਿੰਦੀ ਹੈ।
ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੀਆਂ ਚੁਨੌਤੀਆਂ ਵਿੱਚੋਂ ਇੱਕ ਇਹ ਹੈ ਕਿ ਸਾਰੀ ਥਿਊਰੀ ਅਜੇ ਤੱਕ ਸਾਰੇ ਹਲਾਤਾਂ ਵਿੱਚ ਸੰਤੁਸ਼ਟੀਦਾਇਕ ਪਰਿਭਾਸ਼ਾ ਨਹੀਂ ਦੇ ਸਕੀ| ਸਟਰਿੰਗਾਂ ਦੇ ਖਿੰਡਾਓ ਜਿਆਦਾਤਰ ਸਿੱਧੇ ਹੀ ਗੜਬੜੀ ਸਿਧਾਂਤ (perturbation theory) ਦੀਆਂ ਤਕਨੀਕਾਂ ਵਰਤ ਕੇ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤੇ ਗਏ ਹਨ, ਪਰ ਆਮ ਤੌਰ ਤੇ ਇਹ ਅਗਿਆਤ ਹੈ ਕਿ ਬਗੈਰ ਗੜਬੜੀ ਨਾਲ ਸਟਰਿੰਗ ਥਿਊਰੀ ਨੂੰ ਕਿਵੇਂ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਵੇ| ਇਹ ਵੀ ਸਪਸ਼ਟ ਨਹੀਂ ਹੈ ਕਿ ਕੀ ਕੋਈ ਅਜਿਹਾ ਸਿਧਾਂਤ ਹੈ ਜਾਂ ਨਹੀਂ ਜਿਸ ਨਾਲ ਸਟਰਿੰਗ ‘vacuum state’ (ਪੁਲਾੜ ਅਵਸਥਾ ) ਚੁਣਦੀ ਹੈ, ਜੋ ਸਾਡੇ ਬ੍ਰਹਿਮੰਡ ਦੇ ਗੁਣਾਂ ਨੂੰ ਨਿਰਧਾਰਤ ਕਰਨ ਵਾਲੀ ਸਪੇਸ ਟਾਈਮ ਬਣਤਰ ਹੈ।
ਸਟਰਿੰਗ (ਡੋਰੀ)
[ਸੋਧੋ]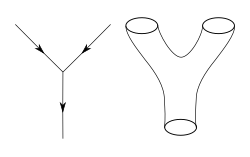
ਕਿਸੇ ਬਿੰਦੂ ਵਰਗੇ ਕਣ ਦੀ ਗਤੀ ਦਰਸਾਉਣ ਲਈ ਇੱਕ ਗਰਾਫ ਤੇ ਇਸਦਾ ਸਥਾਨ ਵਕਤ ਦੇ ਹਿਸਾਬ ਨਾਲ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਨਤੀਜਨ ਤਸਵੀਰ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਉਸਦ ਕਣ ਦੀ ਸੰਸਾਰ-ਰੇਖਾ ਦਰਸਾਏਗੀ| ਇੱਕ ਹੋਰ ਬਰਾਬਰ ਤਰੀਕੇ ਨਾਲ, ਵਕਤ ਦੇ ਗੁਜ਼ਰਨ ਦੇ ਨਾਲ ਨਾਲ ਸਟਰਿੰਗ ਦੀ ਗਤੀ ਨੂੰ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਸਟਰਿੰਗ, ਜੋ ਅਪਣੇ ਆਪ ਵਿੱਚ ਛੋਟੀ ਰੇਖਾ ਵਾਂਗ ਦਿਸਦੇ ਹਨ, ਇੱਕ 2-ਪਸਾਰੀ ਸਤਿਹ ਝਾੜਦੇ ਜਾਂਦੇ ਹਨ ਜਿਸਨੂੰ ਵਰਲਡਸ਼ੀਟ (ਸੰਸਾਰੀ ਚਾਦਰ) ਕਹਿੰਦੇ ਹਨ। ਵੱਖਰੀਆਂ ਸਟਰਿੰਗ ਹਾਲਤਾਂ (ਫੋਟੋਨ ਜਾਂ ਗਰੈਵੀਟੋਨ ਵਰਗੇ ਵੱਖਰੇ ਕਣਾਂ ਨੂੰ ਰਚਦੇ ਹੋਏ) ਇਸ ਸਤਹਿ ਤੇ ਤਰੰਗਾਂ ਵਾਂਗ ਲਗਦੇ ਹਨ।
ਇੱਕ ਬੰਦ ਸਟਰਿੰਗ ਇੱਕ ਛੋਟੇ ਲੂਪ ਵਾਂਗ ਦਿਸਦਾ ਹੈ, ਇਸਲਈ ਇਸਦੀ ਵਰਲਡਸ਼ੀਟ ਪਾਈਪ ਵਾਂਗ ਦਿਸੇਗੀ| ਇੱਕ ਖੁੱਲਾ ਸਟਰਿੰਗ ਦੋ ਸਿਰਿਆਂ ਵਾਲੇ ਛੋਟੇ ਹਿੱਸੇ ਵਾਂਗ ਦਿਸੇਗਾ, ਇਸਲਈ ਇਸਦੀ ਵਰਲਡਸ਼ੀਟ ਇੱਕ ਪੱਟੀ ਵਰਗੀ ਦਿਸੇਗੀ| ਹੋਰ ਜਿਆਦਾ ਗਣਿਤੀ ਭਾਸ਼ਾ ਵਰਤਦੇ ਹੋਏ, ਇਹ ਦੋਵੇਂ ਰਾਈਮਨ ਤਲ (Riemann surfaces) ਹਨ , ਜਿਸ ਵਿੱਚ ਪੱਟੀ ਦੀ ਇੱਕ ਹੱਦ ਹੁੰਦੀ ਹੈ ਪਰ ਪਾਈਪ ਦੀ ਹੱਦ ਨਹੀਂ ਹੁੰਦੀ|
ਸਟਰਿੰਗ ਜੁੜ ਅਤੇ ਟੁੱਟ ਸਕਦੇ ਹਨ। ਇਹ ਉਹਨਾਂ ਦੀ ਵਰਡਲਸ਼ੀਟ ਤੋਂ ਪਤਾ ਚਲਦਾ ਹੈ, ਜਾਂ ਸੰਖੇਪ ਵਿੱਚ ਕਹੀਏ ਤਾਂ ਉਹਨਾਂ ਦੇ ਸਮਸਥਿਤੀ (topology) ਤੋਂ ਪਤਾ ਚਲਦਾ ਹੈ। ਜਿਵੇਂ, ਜੇ ਇੱਕ ਬੰਦ ਸਟਰਿੰਗ ਟੁੱਟਦਾ ਹੈ, ਤਾਂ ਇਸਦੀ ਸੰਸਾਰਸ਼ੀਟ ਇੱਕ ਪਾਈਪ ਦੋ ਪਾਈਪਾਂ ਵਿੱਚ ਤਬਦੀਲ ਹੋਣ ਵਾਂਗ ਗੁਲੇਲ ਵਾਂਗ ਦਿਸਦਾ ਹੈ। ਇਹ ਸਮਸਥਾਨ ਪੈਂਟਾਂ ਦੇ ਜੋੜੇ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਜੇ ਇੱਕ ਬੰਦ ਰਿੰਗ ਟੁੱਟਦਾ ਹੈ ਅਤੇ ਇਸਦੇ ਦੋ ਹਿੱਸੇ ਦੁਬਾਰਾ ਜੁੜਦੇ ਹਨ, ਫੇਰ ਇਸਦੀ ਸੰਸਾਰਸ਼ੀਟ ਇੱਕ ਪਾਈਪ ਦੀ ਤਰਾਂ ਬਣਦੀ ਹੈ ਜੋ ਪਹਿਲਾਂ ਖੁੱਲੇ ਸਿਰੇ ਵਾਲਾ ਹੁੰਦਾ ਹੈ ਫੇਰ ਜੁੜ ਕੇ ਦੁਬਾਰਾ ਉਹੀ ਰਿੰਗ ਬਣ ਜਾਂਦਾ ਹੈ, ਪਰ ਇੱਕ ਹੋਰ ਤਰਾਂ ਦਾ ਰਿੰਗ ਵੀ ਬਣ ਸਕਦਾ ਹੈ ਜੋ ਫੁੱਲ ਵਾਂਗ ਅੱਧਾ ਚੱਕਰ ਹਾਸ਼ੀਏ (torus) ਵਾਂਗ ਦਿਸ ਸਕਦਾ ਹੈ ਜੋ ਦੋ ਪਾਈਪਾਂ ਨੂੰ ਜੁੜਿਆ ਹੁੰਦਾ ਹੈ (ਇੱਕ ਆਉਣ ਵਾਲਾ ਸਟਰਿੰਗ, ਅਤੇ ਦੂਜਾ ਜਾਣ ਵਾਲਾ ਸਟਰਿੰਗ ਦਰਸਾਉਂਦਾ ਹੈ)| ਇੱਕ ਖੁੱਲਾ ਸਟਰਿੰਗ ਜੋ ਅਜਿਹਾ ਹੀ ਕਰ ਰਿਹਾ ਹੋਵੇ ਉਸਦੀ ਵਰਲਡਸ਼ੀਟ ਇੰਝ ਦਿਸ ਸਕਦੀ ਹੈ ਜਿਵੇਂ ਅੰਗੂਠੀ(annulus) ਦੋ ਪੱਟੀਆਂ ਨਾਲ ਜੁੜੀ ਹੁੰਦੀ ਹੈ।
ਕੁਆਂਟਮ ਮਕੈਨਿਕਸ ਵਿੱਚ, ਇੱਕ ਕਣ ਦੀ ਉਦ ਸੰਭਾਵਨਾ ਗਿਣੀ ਜਾਂਦੀ ਹੈ ਜਿਸ ਨਾਲ ਉਹ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਦੂਜੇ ਬਿੰਦੂ ਤੱਕ ਕੁੱਝ ਨਿਸ਼ਚਿਤ ਮੁੱਲਾਂ ਨੂੰ ਜੋੜ ਕੇ ਲੰਘ ਸਕਦਾ ਹੋਵੇ, ਜਿਨਾਂ ਨੂੰ ਸੰਭਾਵ ਅਯਾਮ (probability amplitudes) ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਹਰੇਕ ਅਯਾਮ ਇੱਕ ਕਣ ਦੀ ਸੰਸਾਰ ਰੇਖਾ ਨਾਲ ਜੁੜਿਆ ਹੁੰਦਾ ਹੈ। ਸਾਰੀਆਂ ਸੰਭਵ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਦੇ ਅਯਾਮਾਂ ਦੇ ਜੋੜ ਦੀ ਇਹ ਵਿਧੀ ਰਸਤਾ ਏਕੀਕਰਨ (path integration) ਕਹਾਉਂਦੀ ਹੈ। ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ, ਇੱਕ ਸ਼ੁਰੂਆਤੀ ਸਟਰਿੰਗ ਬਣਤਰ ਤੋਂ ਅੰਤਮ ਸਟਰਿੰਗ ਬਣਤਰ ਤੱਕ ਦੀਆਂ ਸੰਸਾਰਸ਼ੀਟਾਂ ਨਾਲ ਸਬੰਧਤ ਸੰਖਿਆਵਾਂ ਨਾਲ, ਇਸੇ ਤਰਾਂ ਸੰਭਾਵਨਾਵਾਂ ਦਾ ਹਿਸਾਬ ਲਗਦਾ ਹੈ। ਇਹ ਗੱਲ ਸਮਝ ਵਿੱਚ ਹੈ ਕਿ ਸਟਰਿੰਗ ਥਿਊਰੀ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਨੂੰ ਬਿੰਦੂ-ਕਣਾਂ ਦੇ ਸਟਰਿੰਗਾਂ ਵਿੱਚ ਬਦਲਣ ਕਾਰਨ ਹੋਰ ਵਧਾਉਂਦੀ ਹੈ। ਜਿਵੇਂ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਵਿੱਚ, ਫੀਲਡਾਂ ਦੇ ਪੁਰਾਣੇ ਤਰੀਕੇ ਵਿੱਚ ਕਾਰਜ ਦੇ ਫੰਕਸ਼ਨ ਰਾਹੀਂ ਖੇਤਰ ਨਿਰਧਾਰਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਉਵੇਂ ਹੀ ਇਹ ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ ਜਾਂ ਨੰਬੂ-ਗੋਟੋ ਕਾਰਜ ਹੋ ਸਕਦਾ ਹੈ ਜਾਂ ਪੌਲੀਜੋਵ ਕਾਰਜ (Nambu-Goto action or Polyakov action) ਹੋ ਸਕਦਾ ਹੈ।
ਬਰੇਨ (Branes)
[ਸੋਧੋ]
ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ, ਅਤੇ ਮਿਲਦੀਆਂ ਜੁਲਦੀਆਂ ਜਿਵੇਂ ਸੁਪਰਗਰੈਵਿਟੀ ਥਿਊਰੀਆਂ ਵਿੱਚ, ਇੱਕ ਬਰੇਨ ਭੌਤਿਕੀ ਵਸਤੂ ਹੁੰਦੀ ਹੈ ਜੋ ਬਿੰਦੂ ਕਣ ਦੀ ਧਾਰਨਾ ਨੂੰ ਉੱਚੇ ਅਯਾਮਾਂ ਲਈ ਬਰਾਬਰੀਕਰਨ ਕਰਦੀ ਹੈ। ਜਿਵੇਂ, ਇੱਕ ਬਿੰਦੂ ਕਣ 0 ਅਯਾਮ ਵਾਲੇ ਬਰੇਨ ਵਾਂਗ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਜਦੋਂ ਕਿ ਸਟਰਿੰਗ 1 ਅਯਾਮੀ ਬਰੇਨ ਦੀ ਤਰਾਂ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਉੱਚ ਅਯਾਮਾਂ ਵਾਲੇ ਬਰੇਨ ਸੋਚਣੇ ਵੀ ਸੰਭਵ ਹਨ। ਅਯਾਮ (dimension) pਵਿੱਚ ਇਹਨਾਂ ਨੂੰ p-branes ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਬਰੇਨ ਸ਼ਬਦ ‘ਮੈਂਬਰੇਨ’ (membrane) ਤੋਂ ਬਣਾਇਆ ਗਿਆ ਹੈ ਜਿਸਦਾ ਅਰਥ ਹੈ 2ਅਯਾਮੀ ਬਰੇਨ|
ਬਰੇਨ ਗਤੀਸ਼ੀਲ ਵਸਤੂਆਂ ਹਨ ਜੋ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਨੂੰ ਕੁਆਂਟਮ ਮਕੈਨਿਕਸ ਦੇ ਨਿਯਮਾਂ ਮੁਤਾਬਿਕ ਯਾਤਰਾ ਕਰ ਸਕਦੀਆਂ ਹਨ। ਉਹਨਾ ਦਾ ਪੁੰਜ ਹੁੰਦਾ ਹੈ ਅਤੇ ਹੋਰ ਗੁਣ ਵੀ ਹੁੰਦੇ ਹਨ ਜਿਵੇਂ ਚਾਰਜ| ਇੱਕ ਪੀ-ਬਰੇਨ ਸਪੇਸ ਟਾਈਮ ਵਿੱਚ ਇੱਕ (p+1)ਅਯਾਮੀ ਘਣਫਲ (volume) ਦਾ ਸਫਾਇਆ ਕਰਦਾ ਜਾਂਦਾ ਹੈ ਜਿਸਨੂੰ ਉਸ ਬਰੇਨ ਦਾ ਸੰਸਾਰ-ਘਣਫਲ (worldvolume) ਕਹਿੰਦੇ ਹਨ। ਵਿਗਿਆਨੀ ਅਕਸਰ ਬਿਜਲਈ-ਚੁੰਬਕਤਾ (ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਜ਼ਮ) ਖੇਤਰ ਦੇ ਬਰਾਬਰ (analogous) ਦੇ ਖੇਤਰਾਂ ਨੂੰ ਸਟਡੀ ਕਰਦੇ ਹਨ ਜੋ ਇੱਕ ਬਰੇਨ ਦੇ ਵਰਲਡ-ਵੌਲੀਊਮ ਵਿੱਚ ਰਹਿੰਦੇ ਹਨ।
ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ, D-branes ਇੱਕ ਬਰੇਨਾਂ ਦੀ ਮਹੱਤਵਪੂਰਨ ਸ਼੍ਰੇਣੀ ਹੈ ਜੋ ਉਸੋਂ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ਜਦੋਂ ਖੁੱਲੇ ਸਟਰਿੰਗ ਨੂੰ ਲਿਆ ਜਾਂਦਾ ਹੈ। ਜਿਵੇਂ ਇੱਕ ਖੁੱਲਾ ਸਟਰਿੰਗ ਸਪੇਸ ਟਾਈਮ ਵਿੱਚ ਯਾਤਰਾ ਕਰਦਾ ਹੈ,ਇਸਦੇ ਸਿਰੇ ਇੱਕ ਡੀ-ਬਰੇਨ ਵਿੱਚ ਟਿਕੇ ਰਹਿਣੇ ਚਾਹੀਦੇ ਹਨ। ਡੀ ਅੱਖਰ ਇਸ ਸੱਚ ਵੱਲ ਇਸ਼ਾਰਾ ਕਰਦਾ ਹੈ ਕਿ ਅਸੀਂ ਸਿਸਟਮ ਤੇ ਇੱਕ ਗਣਿਤਿਕ ਸ਼ਰਤ ਲਾਗੂ ਕਰ ਦਿੰਦੇ ਹਾਂ ਜਿਸਨੂੰ ਪਹਿਲੀ ਕਿਸਮ ਦੀ ਸ਼ਰਤ (Dirichlet boundary condition) ਕਹਿੰਦੇ ਹਾਂ| ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੀ ਸਟਡੀ ਨੇ ਮਹੱਤਵਪੂਰਨ ਨਤੀਜਿਆਂ ਦੀ ਪ੍ਰੇਰਣਾ ਦਿੱਤੀ ਹੈ ਜਿਵੇਂ AdS/CFT correspondence(?)| ਜਿਸਨੇ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਦੀਆਂ ਬਹੁਤ ਸਮੱਸਿਆਵਾਂ ਨੂੰ ਰਾਹ ਦਿਖਾਇਆ ਹੈ।
ਬਰੇਨਾਂ ਨੂੰ ਇੱਕ ਸ਼ੁੱਧ ਗਣਿਤਿਕ ਨਜ਼ਰੀਏ ਤੋਂ ਵੀ ਵਾਰ ਵਾਰ ਸਟਡੀ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਉਹ ਸਮਾਨ ਦਰਪਣ ਸਮਰੂਪਤਾ ਅਤੇ ਸਥਾਈ ਰੇਖਾਗਣਿਤ (homological mirror symmetry and noncommutative geometry) ਵਰਗੇ ਵਿਸ਼ਿਆਂ ਨਾਲ ਸਬੰਧਿਤ ਹਨ। ਗਣਿਤਿਕ ਤੌਰ ਤੇ, ਬਰੇਨ ਕੁੱਝ ਨਿਸ਼ਚਿਤ ਸ਼੍ਰੇਣੀਆਂ ਦੀਆਂ ਚੀਜਾਂ ਪ੍ਰਸਤੁਤ ਕਰ ਸਕਦੇ ਹਨ, ਜਿਵੇਂ ਇੱਕ ਬਹੁਤ ਜਿਆਦਾ ਕਿਸਮਾਂ ਦੀ ਕੈਲਬੀ-ਯੂ (Calabi-Yau) ਦੇ ਮੇਲ ਖਾਂਦੇ ਢੇਰਾਂ ਵਿੱਚੋਂ ਕੱਢੀ ਗਈ ਸ਼੍ਰੇਣੀ ਜਾਂ ਨਾਲੀ (Fukaya) ਦੀ ਸ਼੍ਰੇਣੀ |
ਡੀ-ਬਰੇਨ (D-branes)
[ਸੋਧੋ]ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ ਡੀ-ਬਰੇਨ ਵਧਾਈਆਂ ਹੋਈਆਂ ਵਸਤੂਆਂ ਦੀ ਉਹ ਸ਼੍ਰੇਣੀ ਹੁੰਦੀ ਹੈ ਜਿਸ ਤੱਕ ਜਾ ਕੇ ਪਹਿਲੀ ਹੱਦ ਤੱਕ ਦੀ ਸ਼ਰਤ ਨਾਲ ਇੱਕ ਖੁੱਲਾ ਸਟਰਿੰਗ ਮੁੱਕ ਸਕਦਾ ਹੈ। ਇਹ ਡਾਈ, ਲੀਗ ਅਤੇ ਪੌਲਚਿੰਸਕੀ ਨੇ ਖੋਜੇ ਸਨ, ਅਤੇ ਹੋਰਵਾਨਾ ਦੁਆਰਾ 1989 ਵਿੱਚ ਇੱਕਲੇ ਨੇ ਹੀ ਖੋਜੇ ਸਨ। 1995 ਵਿੱਚ, ਪੌਲਚਿੰਸਕੀ ਨੇ ਡੀ ਬਰੇਨਾਂ ਨੂੰ ਸੁਪਰਗਰੈਵਿਟੀ ਦੇ ਹੱਲ ਲਈ ਕਾਲੇ- ਪੀ-ਬਰੇਨਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਪਛਾਣਿਆ| ਇਹ ਅਜਿਹੀ ਖੋਜ ਸੀ ਜਿਸਨੇ ਦੂਜੀ ਸੁਪਰਸਟਰਿੰਗ ਇਨਕਲਾਬ ਨੂੰ ਜਨਮ ਦਿੱਤਾ ਅਤੇ ਹੋਲੋਗਰਾਫਿਕ ਤੇ ਐੱਮ ਥਿਊਰੀ ਦੋਹਾਂ ਲਈ ਪ੍ਰੇਰਣਾ ਦਿੱਤੀ|
ਡੀ-ਬਰੇਨ ਅਪਣੇ ਖਾਸ ਅਯਾਮਾਂ ਨਾਲ ਮੂਲ ਰੂਪ ਵਿੱਚ ਸ੍ਰੇਣੀਬੱਧ ਕੀਤੇ ਜਾਂਦੇ ਹਨ, ਜੋ ਡੀ ਦੇ ਨਾਲ ਲਿਖੇ ਨੰਬਰ ਨਾਲ ਦਰਸਾਏ ਜਾਂਦੇ ਹਨ। ਇੱਕ D0-brane ਸਿੰਗਲ ਬਿੰਦੂ ਹੁੰਦਾ ਹੈ, D1-brane ਇੱਕ ਰੇਖਾ ਹੁੰਦੀ ਹੈ ਜਿਸਨੂੰ D-string ਵੀ ਕਹਿ ਸਕਦੇ ਹਾਂ,ਇਸੇ ਤਰਾਂ D2-brane ਇੱਕ ਸਤਹਿ ਹੁੰਦੀ ਹੈ, ਅਤੇ D25-brane ਬੋਸੋਨਿਕ ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ ਉੱਚੇ ਤੋਂ ਉੱਚਾ ਅਯਾਮ ਹੈ। ਸੀਮਤ ਕਾਰਜਹੀਣ ਝੂਠੇ ਬਰੇਨ D(-1)-branes ਵੀ ਹੁੰਦੇ ਹਨ, ਜੋ ਸਪੇਸ ਅਤੇ ਸਮੇਂ ਦੋਹਾਂ ਵਿੱਚ ਸੀਮਤ ਸਥਾਨ ਤੇ ਹੁੰਦੇ ਹਨ।
ਸਿਧਾਂਤਕ ਪਿਛੋਕੜ
[ਸੋਧੋ]ਸਟ੍ਰਿੰਗ ਥਿਊਰੀ ਦੀਆਂ ਗਤੀ ਦੀਆਂ ਸਮੀਕਰਨਾਂ ਨੂੰ ਇਹ ਜਰੂਰਤ ਪੈਂਦੀ ਹੈ ਕਿ ਇੱਕ ਖੁੱਲੇ ਸਿਰਿਆਂ ਵਾਲਾ ਸਟਰਿੰਗ ਨੀਊਮਾਨ ਹੱਦ ਸ਼ਰਤ (Neumann boundary condition) ਦੀਆਂ , ਪ੍ਰਕਾਸ਼ ਦੀ ਗਤੀ ਨਾਲ ਸਪੇਸ ਟਾਈਮ ਰਾਹੀਂ ਗੁਜ਼ਰਦੇ ਵਕਤ ਮੁਕਤ ਸਿਰਿਆਂ ਨਾਲ ਸਬੰਧਤ ਦੋ ਹੱਦਾਂ ਦੀ ਸ਼ਰਤ ਵਿੱਚੋਂ ਇੱਕ ਜਰੂਰ ਪੂਰੀ ਕਰਦਾ ਹੋਵੇ| ਜਾਂ ਪਹਿਲੀ ਕਿਸਮ ਦੀ ਸ਼ਰਤ (Dirichlet boundary conditions) ਪੂਰੀ ਕਰਦਾ ਹੋਵੇ, ਜੋ ਸਟਰਿੰਗ ਦੇ ਸਿਰੇ ਬੰਨ ਕੇ ਰੱਖਦੀ ਹੈ। ਸਟਰਿੰਗ ਦਾ ਹਰੇਕ ਹੁਕਮ-ਅੰਕ (coordinate) ਜਰੂਰ ਹੀ ਇਹਨਾਂ ਸ਼ਰਤਾਂ ਵਿੱਚੋਂ ਇੱਕ ਜਾਂ ਦੂਜੀ ਸ਼ਰਤ ਪੂਰੀ ਕਰਦਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ। ਮਿਕਸ ਹੱਦ ਵਾਲੀਆਂ ਸ਼ਰਤਾਂ ਦੇ ਸਟਰਿੰਗ ਵੀ ਹੋ ਸਕਦੇ ਹਨ, ਜਿੱਥੇ ਦੋਹੇ ਸਿਰੇ NN, DD, ND ਅਤੇ DN ਹੱਦ ਸ਼ਰਤਾਂ ਮੰਨਦੇ ਹੋਣ| ਜੇ p ਸਥਾਨਕ ਅਯਾਮ ਨਿਉਮਨ ਹੱਦ ਸ਼ਰਤ ਪੂਰੀ ਕਰਦਾ ਹੋਵੇ, ਫੇਰ ਉਹ ਸਟਰਿੰਗ ਪੀ-ਅਯਾਮੀ ਹਾਈਪਰ ਸਤਹਿ (p-dimensional hyperplane) ਵਿੱਚ ਗਤੀ ਕਰਨ ਲਈ ਬੰਨਿਆ ਹੋ ਜਾਂਦਾ ਹੈ। ਇਹ ਹਾਈਪਰ ਸਤਹਿ Dp-brane ਦਾ ਇੱਕ ਵਿਵਰਣ ਹੈ।
ਬੇਸ਼ਕ 0 ਬੰਨ ਦੀ ਹੱਦ ਠੋਸ ਹੁੰਦੀ ਹੈ, ਫੇਰ ਵੀ ਖੁੱਲੇ ਸਿਰੇ ਵਾਲਾ ਸਟਰਿੰਗ ਜੋ ਵੱਧ ਤੋਂ ਵੱਧ ਡੀ-ਵਰੇਨ ਤੱਕ ਮੁੱਕ ਸਕਦਾ ਹੈ, ਅਜਿਹਿਆਂ ਅਵਸਥਾਵਾਂ ਰੱਖਦਾ ਹੈ ਜੋ ਇਸਦੇ ਉਤਰਾਅ ਚੜਾਵਾਂ ਨਾਲ ਸਬੰਧਤ ਹੁੰਦੀਆਂ ਹਨ, ਜਿਸਦਾ ਅਰਥ ਹੈ ਡੀ-ਬਰੇਨ ਗਤੀਸ਼ੀਲ ਵਸਤੂਆਂ ਹਨ। ਜਦੋਂ N D ਬਰੇਨ ਲੱਗਭੱਗ ਮੁਨਾਸਬ ਹੁੰਦੇ ਹਨ, ਸਟਰਿੰਗਾਂ ਦੇ ਰੰਗਪਟ ਸਪੈਕਟਰਮ ਦੀ ਖਿੱਚ ਬਹੁਤ ਅਮੀਰ ਬਣ ਜਾਂਦੀ ਹੈ। ਅਜਿਹੀਆਂ ਅਵਸਥਾਵਾਂ ਦਾ ਇੱਕ ਸੈੱਟ ਵਰਲਡ-ਵੌਲੀਅਮਾਂ ਦੀ ਨੌਨ-ਅਬੇਲੀਅਨ ਗੇਜ ਥਿਊਰੀ (ਲਾਪਤਾ ਨਾਪ) ਪੈਦਾ ਕਰਦਾ ਹੈ। ਬਰੇਨ ਦੇ ਹਰੇਕ ਆਡੇ ਅਯਾਮ ਇੱਕ ਹੋਰ ਅਵਸਥਾ ਇੱਕ ਡਬਲ ਸ਼ਰਤ ਗਰਭ-ਅਯਾਮ (N*N) ਅਵਸਥਾ ਹੁੰਦੀ ਹੈ। ਜੇ ਇਹ ਗਰਭ ਅਯਾਮ ਸੁੰਨ (commute) ਕਰ ਦਿੱਤੇ ਜਾਣ, ਤਾਂ ਉਹਨਾਂ ਦਾ ਵਿਕਰਨੀਕਰਨ (diagonalized )ਹੋ ਸਕਦਾ ਹੈ, ਅਤੇ ਖੁਦ ਅਪਣੇ ਆਪ ਦੀ ਈਗਨਵੈਲੀਊ (eigenvalues) ਸਪੇਸ ਵਿੱਚ N D ਬਰੇਨ ਦੀ ਸਥਿਤੀ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰਦੀ ਹੈ। ਹੋਰ ਸਾਫ ਕਹਿੰਦੇ ਹੋਏ, ਬਰੇਨ ਸਥਾਈ ਰੇਖਗਣਿਤ ਰਾਹੀਂ ਦਰਸਾਏ ਜਾਂਦੇ ਹਨ, ਜੋ ਵਿਦੇਸ਼ੀ ਵਰਤਾਓ ਦਿਖਾਉਂਦੇ ਹਨ ਜਿਵੇਂ ਮਾਇਆ (Myers) ਪ੍ਰਭਾਵ, ਜਿਸ ਵਿੱਚ Dp-branes ਦਾ ਇੱਕ ਇਕੱਠ ਫੈਲ ਕੇ D(p+2)-brane ਬਣ ਜਾਂਦਾ ਹੈ।
ਸੰਘਣੀ ਊਰਜਾਹੀਣਤਾ (ਟੈਕੱਨ) (Tachyon condensation) ਇਸ ਖੇਤਰ ਦਾ ਮੁੱਖ ਵਿਚਾਰ ਹੈ। ਇਸ ਪ੍ਰਕ੍ਰਿਆ ਵਿੱਚ ਕੋਈ ਸਿਸਟਮ ਲਗਾਤਾਰ ਕਣ ਪੈਦਾ ਕਰ ਕਰ ਕੇ ਅਪਣੀ ਊਰਜਾ ਘਟਾ ਸਕਦਾ ਹੈ, ਜੋ ਅੰਤ ਨੂੰ ਸਾਰੇ ਸਿਸਟਮ ਨੂੰ ਭਰ ਦਿੰਦੇ ਹਨ, ਤੇ ਸਿਸਟਮ ਸੰਘਣਾ ਹੋ ਜਾਂਦਾ ਹੈ। ਅਸ਼ੋਕ ਸੇਨ ਨੇ ਤਰਕ ਕੀਤਾ ਹੈ ਕਿ Type IIB string theory ਵਿੱਚ, ਟੈਕੱਨ ਕੰਡਨਸੇਸ਼ਨ ( ਨੀਵੀਊ ਸ਼ਵਾਰਜ਼ 3- ਪ੍ਰਵਾਹ ਦੀ ਗੈਰਹਾਜ਼ਰੀ ਵਿੱਚ) D9 ਅਤੇ anti D9-branes ਦੇ ਇੱਕ ਢੇਰ ਤੋਂ ਇੱਕ ਮਨਚਾਹੀ D-brane ਬਣਤਰ ਪ੍ਰਾਪਰ ਕਰਨ ਦੀ ਆਗਿਆ ਦਿੰਦੀ ਹੈ। ਐਡਵਰਡ ਵਿੱਟਨ ਨੇ ਦਿਖਾਇਆ ਕਿ ਅਜਿਹੀਆਂ ਬਣਤਰਾਂ ਸਪੇਸ ਸਮੇਂ ਦੀ ਕੇ-ਥਿਊਰੀ ਦੁਆਰਾ ਸ਼੍ਰੇਣੀ ਬੱਧ ਕੀਤੀਆਂ ਜਾਣਗੀਆਂ| ਟੈੱਕਨ ਕਨਡਸੇਸ਼ਨ ਅਜੇ ਬਹੁਤ ਘੱਟ ਸਮਝੀ ਜਾਂਦੀ ਹੈ। ਇਹ ਇੱਕ ਬਿਲਕੁਲ ਸ਼ੁੱਧ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੀ ਕਮੀ ਕਾਰਨ ਹੈ ਜੋ ਟੈਕੱਨ ਦੀ ਝਿੱਲੀ-ਬੰਦ ਉਤਪੱਤੀ ਨੂੰ ਦਰਸਾ ਸਕਦੀ ਹੋਵੇ|
ਦੋਹਰੇ ਗੁਣ
[ਸੋਧੋ]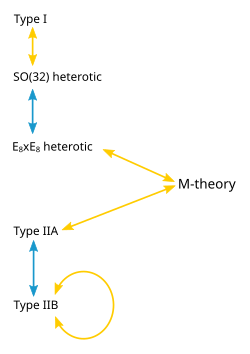
ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ, ਦੋਹਰਾ ਗੁਣ ਅਜਿਹੀ ਪ੍ਰਸਥਿਤੀ ਹੈ ਜਿੱਥੇ ਦੋ ਵੱਖਰੇ ਦਿਸਣ ਵਾਲੇ ਭੌਤਿਕੀ ਸਿਸਟਮ ਇੱਕ ਗੰਭੀਰ ਤਰੀਕੇ ਨਾਲ ਇੰਨਬਿੰਨ ਇੱਕੋ ਜਿਹੇ ਹੋ ਜਾਂਦੇ ਹਨ। ਜੇ ਦੋ ਥਿਊਰੀਆਂ ਨੂੰ ਇੱਕ ਦੋਹਰੇ ਗੁਣ ਨਾਲ ਮਿਲਾ ਦਿੱਤਾ ਜਾਵੇ, ਤਾਂ ਇਸਦਾ ਮਤਲਬ ਹੈ ਕਿ ਇੱਕ ਥਿਊਰੀ ਨੂੰ ਕਿਸੇ ਤਰਾਂ ਤਬਦੀਲ ਕਰਕੇ ਦੂਜੀ ਥਿਊਰੀ ਵਾਂਗ ਦਿਸਣ ਲਗਾਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਫੇਰ ਦੋਵੇਂ ਥਿਊਰੀਆਂ ਤਬਦੀਲੀ ਹੇਠਾਂ ਆਪਸ ਵਿੱਚ ਡਬਲ ਗੁਣ ਵਾਲੀਆਂ ਕਹੀਆਂ ਜਾਂਦੀਆਂ ਹਨ। ਦੋ ਥਿਊਰੀਆਂ ਅਲੱਗ ਤਰੀਕਿਆਂ ਨਾਲ ਰੱਖਣ ਤੇ ਇੱਕੋ ਘਟਨਾ ਦੇ ਵੱਖਰੇ ਵੱਖਰੇ ਗਣਿਤਿਕ ਵਿਵਰਣ ਹੁੰਦੇ ਹਨ।
ਥਿਊਰੀ ਔਫ ਐਵਰੀਥਿੰਗ ਦੇ ਇੱਕ ਸਹਿਭਾਗੀ ਨੂੰ ਸ਼ਾਮਲ ਕਰਨ ਲਈ, ਸਟਰਿੰਗ ਥਿਊਰੀ ਵੱਖਰੀਆਂ ਭੌਤਿਕੀ ਥਿਊਰੀਆਂ ਦਰਮਿਆਨ ਬਹੁਤ ਸਾਰੀਆਂ ਦੋਗਲੇ ਗੁਣਾਂ ਵਾਲੀਆਂ ਉਦਾਹਰਨਾ ਮੁਹੱਈਆ ਕਰਵਾਉਂਦੀ ਹੈ, ਜਿਸ ਕਾਰਨ ਇਹਨਾਂ ਥਿਊਰੀਆਂ ਦਰਮਿਆਨ ਸਬੰਧਾਂ ਨੂੰ ਸਮਝਣ ਲਈ ਇੱਕ ਸ਼ਾਸਤਰ ਦੇ ਤੌਰ ਤੇ ਵਰਤੀ ਜਾ ਸਕਦੀ ਹੈ।
S-, T-, ਅਤੇ U-ਦੋਹਰਾਪਣ
[ਸੋਧੋ]ਇਹ ਸਟਰਿੰਗ ਥਿਊਰੀਆਂ ਦਰਮਿਆਨ ਉਹ ਦੋਹਰੇ ਗੁਣ ਹੁੰਦੇ ਹਨ ਜੋ ਵੱਖਰੇ ਮੁੱਲਾਂ ਨਾਲ ਸਬੰਧਤ ਹੁੰਦੇ ਹਨ। ਵਿਸ਼ਾਲ ਤੇ ਛੋਟੀ ਦੂਰੀ ਦੇ ਪੈਮਾਨੇ, ਅਤੇ ਤਾਕਤਵਰ ਅਤੇ ਕਮਜੋਰ ਬੰਨ ਤਾਕਤਾਂ, ਅਜਿਹੇ ਮੁੱਲ ਹਨ ਜਿਨਾਂ ਨੂੰ ਹਮੇਸ਼ਾਂ ਹੀ ਪੁਰਾਤਨ ਤੇ ਕੁਆਂਟਮ ਫਿਜਿਕਸ ਦੋਹਾਂ ਵਿੱਚ ਇੱਕ ਭੌਤਿਕੀ ਸਿਸਟਮ ਤੇ ਵਤੀਰੇ ਦੀਆਂ ਬਹੁਤ ਵੱਖਰੀਆਂ ਸ਼ਰਤਾਂ ਨਾਲ ਨਿਸ਼ਾਨ ਲਗਾਇਆ ਗਿਆ ਹੈ। ਪਰ ਸਟਰਿੰਗ ਵਿਸ਼ਾਲ/ ਸ਼ਕਤੀਸ਼ਾਲੀ ਤੇ ਸੂਖਮ/ਕਮਜੋਰ ਦਰਮਿਆਨ ਅੰਤਰਾਂ ਨੂੰ ਹਨੇਰਾ ਕਰ ਸਕਦੇ ਹਨ, ਅਤੇ ਇਵੇਂ ਇਹਨਾਂ 5 ਵੱਖਰੀਆਂ ਬਹੁਤ ਮੁਸ਼ਕਲ ਥਿਊਰੀਆਂ ਨੂੰ ਆਪਸ ਵਿੱਚ ਰਲਾਇਆ ਜਾਂਦਾ ਹੈ। T-duality ਵਿਸ਼ਾਲ ਤੇ ਸੂਖਮ ਦੂਰੀਆਂ ਦੇ ਪੈਮਾਨੇ ਨੂੰ ਸਟਰਿੰਗ ਥਿਊਰੀਆਂ ਦੇ ਦਰਮਿਆਨ ਮਿਲਾਉਂਦੀ ਹੈ, ਜਦੋਂਕਿ S-duality ਤਾਕਤਵਰ ਤੇ ਕਮਜੋਰ ਬੰਨ ਨੂੰ ਦੇ ਬਲਾਂ ਨੂੰ ਆਪਸ ਵਿੱਚ ਰਲਾਉਂਦੀ ਹੈ। U-duality ਇਹਨਾਂ ਦੋਵੇਂ T-duality ਅਤੇ S-duality ਨੂੰ ਜੋੜਦੀ ਹੈ।
M-ਥਿਊਰੀ
[ਸੋਧੋ]M-ਥਿਊਰੀ ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ ਇੱਕ ਥਿਊਰੀ ਹੈ ਜੋ ਸੁੱਪਰਸਟਰਿੰਗ ਥਿਊਰੀ ਦੇ ਸਾਰੇ ਸਥਿਰ ਰੂਪਾਂ ਨੂੰ ਇਕੱਠਾ ਕਰਦੀ ਹੈ। ਅਜਿਹੀ ਇੱਕ ਥਿਊਰੀ ਦੀ ਹੋਂਦ ਦਾ ਅਨੁਮਾਨ ਸਭ ਤੋਂ ਪਹਿਲਾਂ 1995 ਦੇ ਬਸੰਤ ਮੌਸਮ ਵਿੱਚ ਦੱਖਣੀ ਕੈਲੀਫੋਰਨੀਆ ਦੀ ਯੂਨੀਵਰਸਟੀ ਵਿਖੇ ਇੱਕ ਸਟਰਿੰਗ ਥਿਊਰੀ ਕਾਨਫਰੰਸ ਵਿੱਚ ਐਡਵਰਡ ਵਿੱਟਨ ਦੁਆਰਾ ਲਗਾਇਆ ਗਿਆ । ਵਿੱਟਨ ਨੇ ਐਲਾਨ ਨੇ ਦੂਜੀ ਸੁੱਪਰਸਟਰਿੰਗ ਕ੍ਰਾਂਤੀ ਦੇ ਨਾਮ ਨਾਲ ਜਾਣੇ ਜਾਂਦੇ ਖੋਜ ਕਾਰਜ ਵਿੱਚ ਉਤੇਜਨਾ ਦੀ ਸ਼ੁਰੂਆਤ ਕਰ ਦਿੱਤੀ ।
1990 ਤੋਂ ਪਹਿਲਾਂ, ਸਟਰਿੰਗ ਵਿਗਿਆਨੀਆਂ ਨੇ ਮੰਨਿਆ ਕਿ 5 ਵੱਖਰੀਆਂ ਸੁਪਰਸਟਰਿੰਗ ਥਿਊਰੀਆਂ ਹਨ: type I, type IIA, type IIB, ਅਤੇ ਹੀਟਰੋਟਿਕ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੇ ਦੋ ਰੂਪ (SO(32) ਅਤੇ E8×E8) ਹਨ। ਸੋਚ ਇਹ ਸੀ ਕਿ ਇਹਨਾਂ 5 ਉਮੀਦਵਾਰ ਥਿਊਰੀਆਂ ਵਿੱਚੋਂ ਸਿਰਫ ਇੱਕ ਸ਼ੁੱਧ ਥਿਊਰੀਔਫਐਵਰਿਥਿੰਗ ਹੈ, ਅਤੇ ਉਹ ਥਿਊਰੀ ਇੱਕ ਉਹ ਸੀ ਜਿਸਦੀ ਨਿਮਰ-ਊਰਜਾ-ਹੱਦ, 10 ਸਪੇਸ ਸਮੇਂ ਦੇ ਅਯਾਮਾਂ ਜੋ 4 ਤੱਕ ਸੁੰਗੇੜੇ ਗਏ ਹਨ, ਸਾਡੇ ਦੇਖੇ ਗਏ ਅੱਜ ਦੇ ਸੰਸਾਰ ਦੀ ਭੌਤਿਕ ਵਿਗਿਆਨ ਨਾਲ ਮੇਲ ਖਾਂਦੇ ਸਨ। ਹੁਣ ਇਹ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਇਹ ਤਸਵੀਰ ਗਲਤ ਸੀ ਤੇ 5- ਸੁਪਰਸਟਰਿੰਗ ਥਿਊਰੀਆਂ ਆਪਸ ਵਿੱਚ ਉੱਪਰ ਦੱਸੇ ਦੋਹਰੇ ਗੁਣਾਂ ਕਾਰਨ ਮੇਲ ਖਾਂਦੀਆਂ ਸਨ। ਇਹਨਾਂ ਦੋਹੇ ਗੁਣਾਂ ਦੀ ਹੋਂਦ ਸੁਝਾਉਂਦੀ ਹੈ ਕਿ 5 ਸਟਰਿੰਗ ਥਿਊਰੀਆਂ ਅਸਲ ਵਿੱਚ ਇੱਕ ਹੋਰ ਮੂਲ M-theory ਦੀਆਂ ਸਪੈਸ਼ਲ ਸ਼੍ਰੇਣੀਆਂ ਹਨ।
ਸਪੇਸ ਸਮਾਂ ਅਯਾਮਾਂ ਦੇ ਮੁਤਾਬਕ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੀਆਂ ਕਿਸਮਾਂ
[ਸੋਧੋ]ਕਿਸਮ – Bosonic
[ਸੋਧੋ]- ਅਯਾਮ- 26
- ਵਿਵਰਣ -ਸਿਰਫ bosons, ਕੋਈ fermions ਨਹੀਂ, ਸਿਰਫ ਬਲਾਂ ਤੱਕ ਮਤਲਬ ਹੈ, ਪਦਾਰਥ ਨਾਲ ਨਹੀਂ, ਖੁੱਲੇ ਤੇ ਬੰਦ ਸਟਰਿੰਗ ;
- ਮੁੱਖ ਦੋਸ਼ : ਇੱਕ ਕਾਲਪਨਿਕ ਕਣ ਜਿਸਨੂੰ, tachyon, ਕਹਿੰਦੇ ਹਨ ਜੋ ਥਿਊਰੀ ਵਿੱਚ ਅਸਥਿਰਤਾ ਪੈਦਾ ਕਰਦਾ ਹੈ।
ਕਿਸਮ-I
[ਸੋਧੋ]- ਅਯਾਮ- 10
- ਵਿਵਰਣ- ਬਲਾਂ ਤੇ ਪਦਾਰਥ ਵਿੱਚ ਸੁਪਰਸਮਰੂਪਤਾ Supersymmetry, ਖੁੱਲੇ ਤੇ ਬੰਦ ਸਟਰਿੰਗ;
- ਕੋਈ ਟੈੱਕਨ ਨਹੀਂ ;
- ਸਮੂਹ ਸਮਰੂਪਤਾ SO(32) ਹੈ।
ਕਿਸਮ-IIA
[ਸੋਧੋ]- ਅਯਾਮ- 10
- ਵਿਵਰਣ- ਬਲਾਂ ਤੇ ਪਦਾਰਥ ਵਿੱਚ ਸੁਪਰ ਸਮਰੂਪਤਾ, ਸਿਰਫ ਬੰਦ ਸਟਰਿੰਗ ਹੀ D-branes ਨਾਲ ਬੰਨੇ ਹੁੰਦੇ ਹਨ ;
- ਕੋਈ ਟੈੱਕਨ ਨਹੀਂ; ਪੁੰਜਹੀਣ fermions ਅਪਣੇ ਅਕਸ ਨਾਲ ਮਿਲਦੇ ਨਹੀਂ ਹੁੰਦੇ|
ਕਿਸਮ- IIB
[ਸੋਧੋ]- ਅਯਾਮ- 10
- ਵਿਵਰਣ- ਬਲਾਂ ਤੇ ਪਦਾਰਥ ਵਿੱਚ ਸੁਪਰਸਮਰੂਪਤਾ , ਸਿਰਫ ਬੰਦ ਸਟਰਿੰਗ ਹੀ D-branes ਨਾਲ ਬੰਨੇ ਹੁੰਦੇ ਹਨ;
- ਕੋਈ ਟੈੱਕਨ ਨਹੀਂ;
- ਪੁੰਜਹੀਣ fermions ਅਪਣੇ ਅਕਸ ਨਾਲ ਮਿਲਦੇ ਹਨ।
ਕਿਸਮ- HO
[ਸੋਧੋ]- ਅਯਾਮ-10
- ਵਿਵਰਣ- ਬਲਾਂ ਤੇ ਪਦਾਰਥ ਵਿੱਚ ਸੁਪਰਸਮਰੂਪਤਾ, ਸਿਰਫ ਬੰਦ ਸਟਰਿੰਗ ਹੀ D-branes ਨਾਲ ਬੰਨੇ ਹੁੰਦੇ ਹਨ;
- ਕੋਈ ਟੈੱਕਨ ਨਹੀਂ;
- heterotic, ਯਾਨਿ ਕਿ ਸੱਜੇ ਤੇ ਖੱਬੇ ਗਤੀਸ਼ੀਲ ਸਟਰਿੰਗ ਵੱਖਰੇ ਹੁੰਦੇ ਹਨ;
- ਸਮੂਹ ਸਮਰੂਪਤਾ SO(32) ਹੈ।
ਕਿਸਮ- HE
[ਸੋਧੋ]- ਅਯਾਮ- 10
- ਵਿਵਰਣ- ਬਲਾਂ ਤੇ ਪਦਾਰਥ ਵਿੱਚ ਸੁਪਰਸਮਰੂਪਤਾ, ਸਿਰਫ ਬੰਦ ਸਟਰਿੰਗ ਹੀ ਹੁੰਦੇ ਹਨ;
- ਕੋਈ ਟੈੱਕਨ ਨਹੀਂ; heterotic,
- ਯਾਨਿ ਕਿ ਸੱਜੇ ਤੇ ਖੱਬੇ ਗਤੀਸ਼ੀਲ ਸਟਰਿੰਗ ਵੱਖਰੇ ਹੁੰਦੇ ਹਨ;
- ਸਮੂਹ ਸਮਰੂਪਤਾ E8×E8 ਹੁੰਦੀ ਹੈ।
ਮੈਟ੍ਰਿਕਸ ਥਿਊਰੀ
[ਸੋਧੋ]ਗਣਿਤ ਵਿੱਚ ਇੱਕ ਮੈਟ੍ਰਿਕਸ ਨੰਬਰਾਂ ਜਾਂ ਹੋਰ ਆਂਕੜੇ ਦੀ ਇੱਕ ਆਇਤਾਕਾਰ ਲੜੀ ਹੁੰਦੀ ਹੈ। ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ, ਇੱਕ ਮੈਟ੍ਰਿਕਸ ਮਾਡਲ ਭੌਤਿਕੀ ਥਿਊਰੀ ਦੀ ਇੱਕ ਖਾਸ ਕਿਸਮ ਹੈ ਜਿਸਦਾ ਗਣਿਤਿਕ ਫਾਰਮੂਲਾ ਸੂਤਰੀਕਰਨ ਮੈਟ੍ਰਿਕਸ ਦੀ ਧਾਰਨਾ ਨੂੰ ਇੱਕ ਮਹੱਤਵਪੂਰਨ ਤਰੀਕੇ ਨਾਲ ਸ਼ਾਮਿਲ ਕਰਦਾ ਹੈ। ਇੱਕ ਮੈਟ੍ਰਿਕਸ ਮਾਡਲ ਮੈਟ੍ਰੀਸੀਜ਼ ਦੇ ਸੈੱਟ ਦੇ ਵਰਤਾੌ ਨੂੰ ਕੁਆਂਟਮ ਮਕੈਨਿਕਸ ਦੇ ਢਾਂਚੇ ਅੰਦਰ ਦਰਸਾਉਂਦਾ ਹੈ।
ਇੱਕ ਮੈਟ੍ਰਿਕਸ ਮਾਡਲ ਦੀ ਇੱਕ ਮਹੱਤਵਪੂਰਨ ਉਦਾਹਰਨ ਟੌਮ ਬੈੰਕਸ, ਵਿੱਲੀ ਫਿਸ਼ਲਰ, ਸਟੀਫਨ ਸ਼ੇਂਕਰ, ਅਤੇ ਲੀਓਨਾਰਡ ਸਸਕਿੰਡ 1997 ਵਿੱਚ ਦੁਆਰਾ ਪ੍ਰਸਤਾਵਿਤ ਕੀਤਾ BFSS ਮੈਟ੍ਰਿਕਸ ਮਾਡਲ ਹੈ। ਇਹ ਥਿਊਰੀ 9 ਵੱਡੇ ਮੈਟ੍ਰਿਕਸਾਂ ਦੇ ਇੱਕ ਸੈੱਟ ਦੇ ਵਰਤਾਓ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ। ਅਪਣੇ ਅਸਲੀ ਪੇਪਰ ਵਿੱਚ, ਇਹਨਾਂ ਲੇਖਕਾਂ ਦੇ ਹੋਰ ਚੀਜ਼ਾਂ ਦੇ ਨਾ ਨਾਲ ਨਾਲ ਦਿਖਾਇਆ ਹੈ ਕਿ, ਇਸ ਮੈਟ੍ਰਿਕਸ ਮਾਡਲ ਦੀ ਨਿਮਰ ਊਰਜਾ ਹੱਦ 11-ਅਯਾਮੀ ਸੁੱਪਰ ਗਰੈਵਿਟੀ ਰਾਹੀਂ ਦਰਸਾਈ ਜਾਂਦੀ ਹੈ। ਇਹਨਾਂ ਗਿਣਤੀਆਂ ਮਿਣਤੀਆਂ ਨੇ ਉਹਨਾਂ ਨੂੰ ਇਹ ਪ੍ਰਸਤੁਤ ਕਰਨ ਦੇ ਯੋਗ ਬਣਾਇਆ ਕਿ BFSS ਮੈਟ੍ਰਿਕਸ ਮਾਡਲ ਇੰਨਿਬਿੰਨ M-ਥਿਊਰੀ ਦੇ ਸਮਾਨ ਹੀ ਹੈ। BFSS ਮੈਟ੍ਰਿਕਸ ਮਾਡਲ ਨੂੰ ਇਸਤਰਾਂ M-ਥਿਊਰੀ ਦੇ ਸਹੀ ਫਾਰਮੂਲਾ ਸੂਤਰੀਕਰਨ ਲਈ ਇੱਕ ਆਦਰਸ਼ ਮੂਲ ਮਾਡਲ ਦੇ ਤੌਰ ਤੇ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ ਅਤੇ ਇੱਕ ਸਰਲ ਸੈਟਿੰਗ ਵਿੱਚ M-ਥਿਊਰੀ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਜਾਂਚਣ ਲਈ ਇੱਕ ਔਜ਼ਾਰ ਦੇ ਰੂਪ ਵਿੱਚ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ।
M-ਥਿਊਰੀ ਦੇ ਮੈਟ੍ਰਿਕਸ ਮਾਡਲ ਫਾਰਮੂਲਾ ਸੂਤਰੀਕਰਨ ਦੇ ਵਿਕਾਸ ਨੇ ਭੌਤਿਕ ਵਿਗਿਆਨੀਆਂ ਨੂੰ ਸਟਰਿੰਗ ਥਿਊਰੀ ਅਤੇ ਨੌਨਕਮਿਊਟੇਟਿਵ ਜੀਓਮੈਟਰੀ ਨਾਮਕ ਗਣਿਤ ਦੀ ਇੱਕ ਸ਼ਾਖਾ ਦਰਮਿਆਨ ਬਹੁਤ ਸਾਰੇ ਸਬੰਧਾਂ ਤੇ ਵਿਚਾਰ ਕਰਨ ਲਈ ਮਜਬੂਤ ਕਰ ਦਿੱਤਾ ਹੈ। ਇਹ ਵਿਸ਼ਾ ਸਧਾਰਨ ਜੀਓਮੈਟਰੀ (ਰੇਖਾਗਣਿਤ) ਦੀ ਇੱਕ ਜਨਰਲਾਈਜ਼ੇਸ਼ਨ ਹੈ ਜਿਸ ਵਿੱਚ ਗਣਿਤ ਸ਼ਾਸਤਰੀ ਨੌਨ-ਕਮਿਊਟੇਟਿਵ ਅਲਜਬਰੇ ਤੋਂ ਔਜ਼ਾਰ ਵਰਤ ਕੇ ਨਵੀਆਂ ਰੇਖਾਗਣਿਤਿਕ ਧਾਰਨਾਵਾਂ ਪਰਿਭਾਸ਼ਿਤ ਕਰਦੇ ਹਨ । 1998 ਤੋਂ ਇੱਕ ਪੇਪਰ ਵਿੱਚ, ਅਲੇਨ ਕੋਨੇਸ, ਮਾਈਕਲ ਆਰ. ਡਗਲਸ, ਅਤੇ ਅਲਬਰਟ ਸ਼ਵਾਰਜ਼ ਨੇ ਦਿਖਾਇਆ ਕਿ ਮੈਟ੍ਰਿਕਸ ਮਾਡਲ ਅਤੇ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੇ ਕੁੱਝ ਪਹਿਲੂ ਇੱਕ ਨੌਨ-ਕਮਿਊਟੇਟਿਵ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਰਾਹੀਂ ਦਰਸਾਏ ਜਾਂਦੇ ਹਨ, ਜੋ ਇੱਕ ਅਜਿਹੀ ਸਪੈਸ਼ਲ ਕਿਸਮ ਦੀ ਭੌਤਿਕੀ ਥਿਊਰੀ ਹੈ ਜਿਸ ਵਿੱਚ ਸਪੇਸਟਾਈਮ ਨੂੰ ਨੌਨਕਮਿਊਟੇਟਿਵ ਜੀਓਮੈਟਰੀ (ਰੇਖਾਗਣਿਤ) ਵਰਤਦੇ ਹੋਏ ਗਣਿਤਿਕ ਤੌਰ ਤੇ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ। ਇਸਨੇ ਇੱਕ ਪਾਸੇ ਤਾਂ ਮੈਟ੍ਰਿਕਸ ਮਾਡਲਾਂ ਅਤੇ M-ਥਿਊਰੀ ਦਰਮਿਆਨ ਸਬੰਧ ਸਥਾਪਿਤ ਕੀਤੇ, ਦੂਜੇ ਪਾਸੇ ਨੌਨਕਮਿਊਟੇਟਿਵ ਜੀਓਮੈਟਰੀ (ਰੇਖਾਗਣਿਤ) ਨਾਲ ਵੀ ਸਬੰਧ ਸਥਾਪਿਤ ਕੀਤੇ । ਇਸਨੇ ਜਲਦੀ ਹੀ ਨੌਨਕਮਿਊਟੇਟਿਵ ਜੀਓਮੈਟਰੀ (ਰੇਖਾਗਣਿਤ) ਅਤੇ ਬਹੁਤ ਸਾਰੀਆਂ ਹੋਰ ਭੌਤਿਕੀ ਥਿਊਰੀਆਂ ਦਰਮਿਆਨ ਹੋਰ ਮਹੱਤਵਪੂਰਨ ਸਬੰਧਾਂ ਦੀ ਖੋਜ ਲਈ ਵੀ ਮਜਬੂਰ ਕੀਤਾ ।
ਵਾਧੂ ਅਯਾਮ
[ਸੋਧੋ]ਅਯਾਮਾਂ ਦੀ ਗਿਣਤੀ
[ਸੋਧੋ]
ਸਟਰਿੰਗ ਥਿਊਰੀ ਦਾ ਮਨਮੋਹਕ ਗੁਣ ਇਹ ਹੈ ਕਿ ਇਹ ਵਾਧੂ ਅਯਾਮਾਂ ਦੀ ਭਵਿੱਖਬਾਣੀ ਕਰਦੀ ਹੈ। ਕਲਾਸੀਕਲ ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ ਅਯਾਮਾਂ ਦੀ ਗਿਣਤੀ ਕਿਸੇ ਨਿਰੰਤਰ ਸਥਿਰ ਮਾਪਦੰਡ ਨਾਲ ਫਿਕਸ ਨਹੀਂ ਸੀ। ਫੇਰ ਵੀ, ਇੱਕ ਚਿਰਸਥਾਈ ਕੁਆਂਟਮ ਥਿਊਰੀ ਬਣਾਉਣ ਲਈ, ਸਟਰਿੰਗ ਥਿਊਰੀ ਨੂੰ ਇੱਕ ਸਪੇਸ ਟਾਈਮ ਵਿੱਚ ਰਹਿਣਾ ਪੈਂਦਾ ਹੈ ਜਿਸ ਨੂੰ ‘ਕਰੀਟੀਕਲ(ਨਾਜੁਕ) ਅਯਾਮ’ ਕਹਿੰਦੇ ਹਨ: ਇਸ ਵਿੱਚ ਕੋਈ ਵੀ ਚੀਜ਼ ਦਾ ਠੋਸ, ਦ੍ਰਵ, ਗੈਸ ਤੇ ਪਲਾਜ਼ਮਾ ਅਵਸਥਾ ਵਾਲਾ ਗੁਣ ਬਦਲ ਜਾਂਦਾ ਹੈ; ਇਸ ਲਈ ਸਾਡੇ ਕੋਲ ਸਪੇਸ ਟਾਈਮ ਦੇ 26 ਅਯਾਮ ਬੋਸਨੋਕ ਸਟਰਿੰਗ ਦੇ ਅਤੇ 10 ਸੁਪਰਸਟਰਿੰਗ ਦੇ ਹੋਣੇ ਜਰੂਰੀ ਹਨ। ਇਹ ਅਨੁਕੂਲਤਾ ਖੇਤਰ ਥਿਊਰੀ (conformal field theory) ਵਾਲੀ ਵਰਲਡਸ਼ੀਟ ਦੀ ਗਤੀ ਵਿਰੋਧੀ-ਅਨੁਕੂਲਤਾ ਦੇ ਅੰਤ ਨੂੰ ਯਕੀਨੀ ਬਣਾਉਣ ਲਈ ਜਰੂਰੀ ਹੈ। ਅਜੋਕੀ ਸਮਝ ਇਸ਼ਾਰਾ ਕਰਦੀ ਹੈ ਕਿ ਇਸ ਸ਼ਰਤ ਨੂੰ ਪੂਰਾ ਕਰਨ ਲਈ ਜਰਾ ਗੰਭੀਰ ਰਸਤੇ ਹੁੰਦੇ ਹਨ ਤੇ ਸੌਖੇ ਰਸਤੇ ਘੱਟ ਹੁੰਦੇ ਹਨ। ਬ੍ਰਹਿਮੰਡੀ ਹੱਲ ਅਯਾਮਾਂ ਦੀ ਬਹੁਤ ਵਿਸ਼ਾਲ ਵੈਰਾਈਟੀ ਵਿੱਚ ਮੌਜੂਦ ਹੁੰਦੇ ਹਨ, ਅਤੇ ਇਹ ਵੱਖਰੇ ਅਯਾਮ ਗਤੀਸ਼ੀਲ ਸ਼ਕਤੀਸ਼ਾਲੀ ਤਬਦੀਲੀਆਂ ਨਾਲ ਸਬੰਧ ਰੱਖਦੇ ਹਨ(ਤੁਲਨਾਤਮਿਕ ਹੁੰਦੇ ਹਨ)| ਇਹ ਅਯਾਮ ‘ਪ੍ਰਭਾਵਸ਼ਾਲੀ ਕੇਂਦਰੀ ਚਾਰਜ’ ਦੇ ਹੋਰ ਜਿਆਦਾ ਨਿਸ਼ਚਿਤ ਵੱਖਰੇ ਮੁੱਲ ਹਨ, ਕਮਜੋਰ ਸ਼ਾਸਨ-ਪਲਟ ਮੋੜ (curved regimes) ਵਿੱਚ ਅਯਾਮਾਂ ਦੀ ਕਮੀ ਦੀ ਅਜਾਦੀ ਦੀ ਡਿਗਰੀ ਦੀ ਗਿਣਤੀ ਹੈ।
ਇੱਕ ਅਜਿਹੀ ਥਿਊਰੀ 11 ਅਯਾਮੀ M-theory ਹੈ, ਜੋ ਸਪੇਸ ਟਾਈਮ ਦੇ 11 ਅਯਾਮ ਮੰਗਦੀ ਹੈ, ਜੋ ਆਮ 3 ਸਥਾਨਿਕ ਅਯਾਮਾਂ ਅਤੇ 4 ਵਕਤ ਦੇ ਅਯਾਮ ਤੋਂ ਉਲਟ ਹੈ। 1980 ਤੋਂ ਬਾਦ ਦੀਆਂ ਮੂਲ ਸਟਰਿੰਗ ਥਿਊਰੀਆਂ ਇਸ ਥਿਊਰੀ ਦਾ ਖਾਸ ਕੇਸ ਦਰਸਾਉਂਦੀਆਂ ਹਨ ਜਿੱਥੇ 11ਵਾਂ ਅਯਾਮ ਬਹੁਤ ਸੂਖਮ ਚੱਕਰ ਜਾਂ ਰੇਖਾ ਹੁੰਦੀ ਹੈ, ਤੇ ਜੇਕਰ ਇਹਨਾਂ ਫਾਰਮੂਲਿਆਂ ਬਣਤਰਾਂ ਨੂੰ ਮੂਲ ਰੂਪ ਵਿੱਚ ਲਿਆ ਜਾਵੇ, ਤਾਂ ਸਟਰਿੰਗ ਥਿਊਰੀ ਨੂੰ 10ਅਯਾਮਾਂ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ। ਪਰ ਫੇਰ ਥਿਊਰੀ ਸਾਡੇ ਵਰਗੇ ਬ੍ਰਹਿਮੰਡ ਵੀ ਦਰਸਾਉਂਦੀ ਹੈ, ਜਿਹਨਾਂ ਵਿੱਚ ਸਪੇਸ ਸਮੇਂ ਦੇ 4 ਦਿਸਣਯੋਗ ਅਯਾਮ ਹੁੰਦੇ ਹਨ ਅਤੇ ਅਜਿਹੇ ਬ੍ਰਹਿਮੰਡ ਵੀ ਦਰਸਾਉਂਦੀ ਹੈ ਜਿਹਨਾਂ ਵਿੱਚ 10 ਪੱਧਰੀ ਸਪੇਸ ਦੇ ਅਯਾਮਾਂ ਹੁੰਦੇ ਹਨ, ਅਤੇ ਜਿਹੇ ਕੇਸ ਵੀ ਦਰਸਾਉਂਦੀ ਹੈ ਜਿੱਥੇ ਕੁੱਝ ਅਯਾਮਾਂ ਵਿੱਚ ਪੁਜੀਸ਼ਨ ਨੂੰ ਵਾਸਤਵਿਕ ਅੰਕ ਨਾਲੋਂ ਕੰਪਲੈਕਸ ਨੰਬਰ ਨਾਲ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ। ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ ਸਪੇਸਟਾਈਮ ਦੀ ਧਾਰਨਾ ਫਿਕਸ ਨਹੀਂ ਕੀਤੀ ਗਈ ਹੈ: ਇਹ ਵੱਖਰੇ ਹਲਾਤਾਂ ਵਿੱਚ ਵੱਖਰੇ ਜਿਆਦਾ ਵਧੀਆ ਸੋਚੇ ਗਏ ਹਨ।
ਮੈਕਸਵੈੱਲ ਦੀ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਜ਼ਮ ਦੀ ਥਿਊਰੀ ਵਿੱਚ, ਜਾਂ ਆਈਨਸਟਾਈਨ ਦੀ ਰਿਲੇਟਿਵਿਟੂ ਥਿਊਰੀ ਵਿੱਚ ਅਜਿਹੀ ਕੋਈ ਭਵਿੱਖਬਾਣੀ ਨਹੀਂ ਕੀਤੀ ਜਾਂਦੀ: ਇਹ ਥਿਊਰੀਆਂ ਵਿਗਿਆਨੀਆਂ ਨੂੰ ਮਾਨਸਿਕ ਤੌਰ ਤੇ ਮਨਚਾਹੇ ਅਯਾਮ ਭਰਨ ਦੀ ਜਰੂਰਤ ਮੰਗਦੀਆਂ ਹਨ ਅਤੇ ਇਹ ਨੰਬਰ ਫਿਕਸ ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਪੁਟੈਂਸ਼ਲ (ਸੰਭਾਵਨਾ, ਤਨਾਓ, ਸਥਾਨਿਕ, ਕਾਰਜਯੋਗਤਾ) ਊਰਜਾ ਤੋਂ ਮੁਕਤ ਰਹਿੰਦਾ ਹੈ। ਤਕਨੀਕੀ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਇਹ ਵਾਪਰਦਾ ਹੈ ਕਿਉਂਕਿ ਭਵਿੱਖਤ ਅਯਾਮਾਂ ਦੇ ਹਰੇਕ ਵੱਖਰੇ ਨੰਬਰ ਲਈ ਨਾਪ-ਅਸ਼ੁਧੱਤਾ gauge anomaly ਮੌਜੂਦ ਹੁੰਦੀ ਹੈ, ਤੇ ਇਸ ਅਸ਼ੁੱਧਤਾ ਨੂੰ ਘੱਟ ਕਰਨ ਲਈ ਗਤੀ ਹੱਲ ਕਰਨ ਵਾਲੀਆਂ ਸਮੀਕਰਨਾਂ ਵਿੱਚ ਗੰਭੀਰ ਪੁਟੈਂਸਲ ਊਰਜਾ ਨੂੰ ਸ਼ਾਮਿਲ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਹੋਰ ਅੱਗੇ, ‘ਨਾਜੁਕ ਅਯਾਮਾਂ’ ਵਿੱਚ ਪੁਟੈਂਸ਼ਲ ਊਰਜਾ ਦੀ ਗੈਰਹਾਜ਼ਰੀ ਦੱਸਦੀ ਹੈ ਕਿ ਕਿਉਂ ਪੱਧਰੇ ਸਪੇਸ ਸਮੇਂ ਹੱਲ ਸੰਭਵ ਹਨ।
ਇਹ ਇਸ ਗੱਲ ਨੂੰ ਨੋਟ ਕਰਕੇ ਵਧੀਆ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਇੱਕ ਸਥਾਈ ਥਿਊਰੀ ਵਿੱਚ ਸ਼ਾਮਲ ਫੋਟੋਨ (ਤਕਨੀਕੀ ਤੌਰ ਤੇ ਇੱਕ ਬਲ ਨੂੰ ਸਵਾਰੀ ਕਰਵਾਉਣ ਵਾਲਾ ਕਣ ਜੋ ਨਾ-ਤੋੜੇ ਜਾ ਸਕਣ ਵਾਲੀ ਗੇਜ ਸਮਿੱਟਰੀ ਨਾਲ ਸਬੰਧਿਤ ਹੈ) ਜਰੂਰ ਪੁੰਜਹੀਣ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ। ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੁਆਰਾ ਭਵਿੱਖਤ ਕੀਤਾ ਫੋਟੋਨ ਦਾ ਪੁੰਜ ਸਟਰਿੰਗ ਦੀ ਫੋਟੋਨ ਪ੍ਰਸਤੁਤ ਕਰਨ ਵਾਲੀ ਅਵਸਥਾ ਤੇ ਨਿਰਭਰ ਹੈ। ਇਹ ਊਰਜਾ ਕੈਸੀਮਰ ਪ੍ਰਭਾਵ (Casimir effect) ਯੋਗਾਦਾਨ ਕਾਰਨ ਹੁੰਦੀ ਹੈ , ਜਿਸਨੂੰ ਸਟਰਿੰਗ ਵਿੱਚ ਕੁਆਂਟਮ ਉਤਰਅ-ਚੜਾਓ ਤੋਂ ਨਾਮ ਦਿੱਤਾ ਗਿਆ| ਇਸ ਯੋਗਦਾਨ ਦਾ ਅਕਾਰ ਅਯਾਮਾਂ ਦੇ ਨੰਬਰ ਤੇ ਨਿਰਭਰ ਹੈ, ਕਿਉਂਕਿ ਅਯਾਮਾਂ ਦੇ ਵਿਸ਼ਾਲ ਨੰਬਰ ਲਈ ਸਟਰਿੰਗ ਦੀ ਪੁਜੀਸ਼ਨ ਵਿੱਚ ਹੋਰ ਸੰਭਵ ਉਤਰਾਅ ਚੜਾਓ ਹੋ ਸਕਦੇ ਹਨ। ਇਸਲਈ, ਪੱਧਰੇ (ਫਲੈਟ)ਅਯਾਮ ਵਿੱਚ ਫੋਟੋਨ ਪੁੰਜਹੀਣ ਹੋਵੇਗਾ- ਤੇ ਥਿਊਰੀ ਸਥਿਰ ਕਰਨ ਵਾਲਾ ਸਿਰਫ ਕੁੱਝ ਖਾਸ ਅਯਾਮਾਂ ਦੇ ਨੰਬਰ ਲਈ ਹੀ ਹੋਵੇਗਾ| ਜਦੋਂ ਕੈਲਕੁਲੇਸ਼ਨ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ਤਾਂ ਨਾਜੁਕ ਅਯਾਮ ਅਵਸਥਾ 4 ਨਹੀਂ ਹੁੰਦੀ ਜਿਵੇਂ ਕੋਈ ਉਮੀਦ ਰੱਖ ਸਕਦਾ ਹੈ (3 ਸਪੇਸ ਦੇ ਅਯਾਮ+1 ਵਕਤ ਦਾ ਅਯਾਮ)| X-ਦਾ ਉਪ ਸਮੂਹ ਫੋਟੋਨ ਦੀਆਂ ਰੇਖਿਕ ਅਯਾਮ ਵਿੱਚ ਲਹਿਰਾਂ ਬਰਾਬਰ ਹੈ। ਬੋਸੋਨਾਂ ਦੇ ਕੇਸ ਵਿੱਚ ਫਲੈਟ ਸਪੇਸ ਸਟਰਿੰਗ ਥਿਊਰੀਆਂ 26-ਅਯਾਮੀ ਹਨ, ਜਦੋਂ ਕਿ ਸੁਪਰਸਟਰਿੰਗ ਤੇ ਐੱਮ-ਥਿਊਰੀਆਂ ਨੇ ਇਹਨਾਂ ਲਈ 10 ਜਾਂ 11 ਅਯਾਮ ਹੀ ਪੱਧਰੇ ਹੱਲਾਂ ਲਈ ਰੱਖੇ ਹਨ।
ਬੋਸਨੋਕਿ ਸਟਰਿੰਗ ਥਿਊਰੀਆਂ ਵਿੱਚ 26ਅਯਾਮ ਪੌਲੀਕੋਵ ਸਮੀਕਰਨ ਤੋਂ ਬਣਦੇ ਹਨ। 4 ਤੋਂ ਜਿਆਦਾ ਅਯਾਮਾਂ ਤੋਂ ਸ਼ੁਰੂ ਕਰਨ ਲਈ ਇਹ ਸੋਚਣਾ ਜਰੂਰੀ ਹੈ ਕਿ ਇਹ 4 ਅਯਾਮੀ ਸਪੇਸ ਟਾਈਮ ਵਿੱਚ ਕਿਵੇਂ ਸੁੰਗੇੜੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ।
ਸੂਖਮ ਸੁੰਗੜੇ ਪਸਾਰ
[ਸੋਧੋ]ਕਾਲਾਬਿ-ਯਾਓ ਮੈਨੀਫੋਲਡ
[ਸੋਧੋ]
ਇਸ ਸਪਸ਼ਟ ਅੰਤਰਵਿਰੋਧ ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ 2 ਤਰੀਕੇ ਰੱਖੇ ਗਏ ਹਨ। ਪਹਿਲਾ ਵਾਧੂ ਅਯਾਮਾਂ ਨੂੰ ਸੂਖਮ ਬਣਾਉਣਾ; 6 ਜਾਂ 7 ਵਾਧੂ ਅਯਾਮ ਇੰਨੇ ਸੂਖਮ ਹੁੰਦੇ ਹਨ ਕਿ ਅਜੋਕੇ ਪ੍ਰਯੋਗ ਜਾਂਚ ਨਹੀਂ ਸਕਦੇ|
ਸੁਪਰਸਮਿੱਟਰੀ ਦਾ ਉੱਚਾ ਦਰਜਾ ਪ੍ਰਾਪਤ ਕਰਨ ਲੈਣ ਲਈ, ਇਹ ਸੁੰਗੜੀ ਹੋਈ ਸੂਖਮ ਸਪੇਸ ਜਰੂਰ ਹੀ ਬਹੁਤ ਸਪੈਸ਼ਲ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ, ਜਿਵੇਂ ਉਹਨਾਂ ਦੀ ਹੋਲੋਨੋਮੀ (holonomy) ( ਗੋਲੇ ਤੇ ਕਿਸੇ ਖਾਸ ਰਸਤੇ ਤੇ ਨਿਰਭਰ ਬਲ ਦੀ ਸਮਾਂਤਰ ਸਵਾਰੀ ਦੀ ਯੋਗਤਾ)ਤੋਂ ਪਤਾ ਚਲਦਾ ਹੈ। ਇੱਕ 6ਅਯਾਮੀ ਬਹੁ-ਪਰਤ ਜਰੂਰ ਹੀ SU(3) ਬਣਤਰ ਵਾਲੀ ਹੋਵੇਗੀ, ਜੋ SU(3) ਹੋਲੋਮੋਨੀ ਦਾ ਸਪੈਸ਼ਲ ਕੇਸ ਹੈ ਜਿਸ ਨੂੰ ਮਰੋੜੀ ਨਹੀਂ ਦਿੱਤੀ ਜਾ ਸਕਦੀ (torsionless), ਤੇ ਇਸਨੂੰ ਕੈਲਬੀ- ਯਾਊ ਬਹੁਪਰਤ Calabi–Yau ਸਪੇਸ ਬਣਾ ਦਿੰਦਾ ਹੈ, ਤੇ ਇੱਕ 7 ਅਯਾਮੀ ਬਹੁਤ-ਪਰਤ ਜਰੂਰ ਹੀ G2 ਬਣਤਰ ਵਾਲੀ ਹੋਵੇਗੀ , ਜਿਸ ਨਾਲ ਉਹ G2 holonomy ਨਾਲ ਫੇਰ ਤੋਂ ਸਰਲ ਸਪੈਸ਼ਲ ਕੇਸ ਬਣ ਜਾਂਦੀ ਹੈ। ਅਜਿਹੀਆਂ ਸਪੇਸਾਂ ਇਸ ਮੰਤਵ ਲਈ ਸਟਡੀ ਕੀਤੀਆਂ ਗਈਆਂ ਹਨ ਤਾਂ ਹੋ ਸਟਰਿੰਗ ਥਿਊਰੀ ਨੂੰ 4-ਅਯਾਮੀ ਸਟੈਂਡਰਡ ਮਾਡਲ ਨਾਲ ਅੰਸ਼ਿਕ ਤੌਰ ਤੇ ਗਿਣਤੀ ਦੀ ਸਰਲਤਾ ਲਈ ਸੁਪਰਸਮਿਟਰੀ ਦੀ ਧਾਰਨਾ ਕਰ ਸਕਣ ਲਈ ਤੁਲਨਾਤਮਕ ਬਣਾਇਆ ਜਾ ਸਕੇ|
ਬਹੁ-ਅਯਾਮੀ ਸਪੇਸ ਨੂੰ ਸਮਝਣ ਲਈ ਇੱਕ ਬਗੀਚੇ ਦੇ ਰਬੜ ਦੇ ਪਾਈਪ ਦੀ ਇੰਨਬਿੰਨ ਸਟੈਂਡਰਡ ਉਦਾਹਰਨ ਹੈ। ਜੇਕਰ ਪਾਈਪ ਜਰੂਰੀ ਮਾਤਰਾ ਦੀ ਦੂਰੀ ਤੋਂ ਦੇਖਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਹ ਸਿਰਫ 1 ਅਯਾਮੀ ਲਗਦਾ ਹੈ ਜੋ ਇਸਦੀ ਲੰਬਾਈ ਹੁੰਦੀ ਹੈ। ਸੱਚਮੁੱਚ, ਇੱਕ ਗੇਂਦ ਬਾਰੇ ਸੋਚੋ ਜੋ ਇੰਨੀ ਛੋਟੀ ਹੋਵੇ ਕਿ ਪਾਈਪ ਵਿੱਚ ਨੂੰ ਦਾਖਲ ਹੋ ਸਕਦੀ ਹੋਵੇ| ਅਜਿਹੀ ਗੇਂਦ ਨੂੰ ਪਾਈਪ ਵਿੱਚ ਸੁੱਟਣ ਤੇ , ਗੇਂਦ ਇੱਕ ਅਯਾਮ ਵਿੱਚ ਘੱਟ ਜਾਂ ਵੱਧ ਗਤੀ ਕਰ ਸਕੇਗੀ; ਕਿਸੇ ਵੀ ਪ੍ਰਯੋਗ ਵਿੱਚ, ਅਸੀਂ ਪਾਈਪ ਵਿੱਚ ਅਜਿਹੀਆਂ ਗੇਂਦਾਂ ਸੁੱਟਣ ਨਾਲ, ਜਰੂਰੀ ਮਹੱਤਤਾ ਵਾਲੀ ਗਤੀ ਸਿਰਫ 1 ਅਯਾਮੀ ਹੋਵੇਗੀ, ਯਾਨਿ ਕਿ, ਪਾਈਪ ਦੇ ਨਾਲ ਨਾਲ ਹੋਵੇਗੀ| ਫੇਰ ਵੀ, ਜਿਵੇਂ ਹੀ ਕੋਈ ਪਾਈਪ ਦੇ ਨੇੜੇ ਪਹੁੰਚ ਕੇ ਦੇਖਦਾ ਹੈ ਤਾਂ ਖੋਜਦਾ ਹੈ ਕਿ ਇਸਦਾ ਦੂਜਾ ਅਯਾਮ ਵੀ ਹੈ, ਜੋ ਇਸਦਾ ਘੇਰਾ(ਗੋਲਾਈ) ਹੁੰਦਾ ਹੈ। ਤਾਂ ਫੇਰ, ਇਸਦੇ ਅੰਦਰ ਤੁਰਦਾ ਇੱਕ ਕੀੜਾ 2 ਅਯਾਮਾਂ ਵਿੱਚ ਗਤੀ ਕਰ ਸਕਦਾ ਹੋਵੇਗਾ (ਅਤੇ ਇਸਦੇ ਅੰਦਰ ਉਡਦੀ ਇੱਕ ਮੱਖੀ 3 ਅਯਾਮਾਂ ਵਿੱਚ ਗਤੀ ਕਰ ਸਕਦੀ ਹੋਵੇਗੀ)| ਇਹ ਵਾਧੂ ਅਯਾਮ ਦੀ "extra dimension" ਸਿਰਫ ਇੱਕ ਤੁਲਨਾਤਮਕ ਨਜ਼ਦੀਕੀ ਪਾਈਪ ਦੇ ਖੇਤਰ ਤੋਂ ਹੀ ਦੇਖੀ ਜਾਣ ਜੋਗੀ ਹੋਵੇਗੀ, ਜਾਂ ਜੇ ਕੋਈ ਇਨਸਾਨ ਇਸ ਵਿੱਚ ਜਰੂਰੀ ਮਾਤਰਾ ਵਿੱਚ ਛੋਟੀਆਂ ਚੀਜਾਂ ਸੁੱਟਦਾ ਹੈ, ਤਾਂ ਦੇਖੀ ਜਾ ਸਕੇਗੀ| ਇਸੇ ਤਰਾਂ, ਵਾਧੂ ਸੂਖਮ ਅਯਾਮ ਸਿਰਫ ਛੋਟੀਆਂ ਸੂਖਮ ਦੂਰੀਆਂ ਤੋਂ ਹੀ ਦੇਖੇ ਜਾ ਸਕਦੇ ਹਨ, ਜਾਂ ਫੇਰ ਅਜਿਹੇ ਕਣਾਂ ਦੇ ਨਾਲ ਪ੍ਰਯੋਗ ਕਰਕੇ ਸੰਭਵ ਹੋ ਸਕਦਾ ਹੈ ਜਿਹਨਾਂ ਦੀਆਂ ਤਰੰਗ ਲੰਬਾਈਆਂ wavelengths ( ਸੂਖਮ ਸੁੰਗੜੇ ਅਯਾਮ ਦੇ ਅਰਧ ਵਿਆਸ ਦੀ ਵਿਵਸਥਾ ਦੀਆਂ ਵੇਵਲੈਂਥਾਂ ਨਾਲ) ਅੱਤ ਦਰਜੇ ਤੱਕ ਜਰੂਰੀ ਸੂਖਮ ਹੋਣ, ਜਿਨਾਂ ਨੂੰ ਕੁਆਂਟਮ ਮਕੈਨਿਕਸ ਵਿੱਚ ਉੱਚ ਉਰਜਾਵਾਂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।
ਬਰੇਨ ਸੰਸਾਰ ਕਥਾ
[ਸੋਧੋ]ਇੱਕ ਹੋਰ ਸੰਭਾਵਨਾ ਇਹ ਹੈ ਕਿ ਅਸੀਂ ਪੂਰੇ ਬ੍ਰਹਿਮੰਡ ਦੀ 3+1 ਅਯਾਮੀ ਉਪ-ਸਪੇਸ (3 ਪੁਜੀਸ਼ਨ ਦੇ ਅਯਾਮ+1 ਵਕਤ ਦਾ ਅਯਾਮ) ਵਿੱਚ ਫਸ ਗਏ ਹਾਂ| ਸੁਆਰ ਕੇ ਪੁਜੀਸ਼ਨ ਤੇ ਰੱਖਿਆ ਪਦਾਰਥ ਅਤੇ ਯਾਂਗ-ਮਿੱਲਜ਼ ਗੇਜ (Yang–Mills gauge) ਫੀਲਡਾਂ ਮੂਲ ਰੂਪ ਵਿੱਚ ਮੌਜੂਦ ਹੋਣਗੀਆਂ ਜੇ ਸਬ-ਸਪੇਸਸਮਾਂ ( ਉੱਪ ਸਪੇਸ ਟਾਈਮ) ਜਿਆਦਾ ਵੱਡੇ ਬ੍ਰਹਿਮੰਡ ਦਾ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਸੈੱਟ ਹੋਵੇ| ਇਹ ਸਪੈਸ਼ਲ ਸੈੱਟ ਕਲਾਬੀ-ਯੂ n-folds ਵਿੱਚ ਸਰਵ ਵਿਆਪਕ ਹਨ ਅਤੇ ਸਥਾਨਿਕ ਤੋੜਮਰੋੜ ਤੋਂ ਬਗੈਰ ਵਾਲੀਆਂ ਸਬਸਪੇਸਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਦਰਸਾਏ ਜਾ ਸਕਦੇ ਹਨ, ਜੋ ਪੇਪਰ ਦੀ ਸ਼ੀਟ ਦੀ ਝੁਰੜੀ ਦੇ ਵਾਂਗ ਹਨ ਜਾਂ ਕਿਸੇ ਵਧੀਆ ਕੰਚ ਦੀ ਤਰੇੜ ਵਾਂਗ ਹਨ, ਜਿਸਦੇ ਗਵਾਂਢ ਵਿੱਚ ਸਪਸ਼ਟ ਰੂਪ ਵਿੱਚ ਸਪੈਸ਼ਲ ਸਬਸਪੇਸ ਦੇ ਅਪਣੇ ਆਪ ਤੋਂ ਵੱਖਰੀ ਸਪੇਸ ਹੈ। ਫੇਰ ਵੀ, ਰੰਡਲ ਤੇ ਸੁੰਦਰਮ ਦੇ ਕੰਮ ਤੱਕ ਇਹ ਅਗਿਆਤ ਸੀ ਕਿ ਗਰੈਵਟੀ ਵੀ ਸਬਸਪੇਸ ਸਮੇਂ ਤੱਕ ਪੁਜੀਸ਼ਨ-ਬੱਧ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ। ਇਸਦੇ ਨਾਲ ਹੀ, ਸਪੇਸ ਸਮੇਂ ਨੂੰ ਪਰਤਾਂ ਵਿੱਚ ਵਿਵਸਿਥ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਜਿਸ ਵਿੱਚ ਵਿਭਿੰਨ ਅਯਾਮਾਂ ਦੀਆਂ ਪਰਤਾਂ ਦਾ ਸਤਰ ਹੋਵੇ, ਜੋ ਸਾਨੂੰ 3+1-ਅਯਾਮੀ ਚਾਦਰ ਵਿੱਚ ਨਿਵਾਸ ਕਰਨ ਦੀ ਆਗਿਆ ਦਿੰਦਾ ਹੈ- ਅਜਿਹੇ ਰੇਖਾ ਗਣਿਤ ਕੁਦਰਤੀ ਤੌਰ ਤੇ ਕਾਲਾਬੀ-ਯੂ ਸੁੰਗੇੜਨਾਂ ਵਿੱਚ ਪਾਇਆ ਜਾਂਦਾ ਹੈ। ਅਜਿਹੇ ਸਬਸਪੇਸਸਮੇ D-ਬਰੇਨ ਹਨ, ਜਿਸ ਕਾਰਨ ਅਜਿਹੇ ਮਾਡਲ ਬਰੇਨ ਸੰਸਾਰ ਸਮਾਨ ਜਾਣੇ ਜਾਂਦੇ ਜਨ| ਜਿਸਨੂੰ ਹਿੰਦੀ ਵਿੱਚ अम्कऋ अंक आदि के टम का विवरण (ਅਰੰਭਿਕ ਅੰਕ ਪ੍ਰਣਾਲੀ ਦਾ ਵਿਵਰਣ) ਕਹਿੰਦੇ ਹਨ। ਪੰਜਾਬੀ ਵਿੱਚ ਬਰੇਨ ਸੰਸਾਰ ਪ੍ਰਤਿਬਿੰਬਾਂ ਦੇ ਦ੍ਰਿਸ਼ ਕਹਿੰਦੇ ਹਨ। अम्कऋ ਅੰਰਭ ਦੇ ਅਵਾਜ਼ ਦਾ ਵਿਵਰਣ ਵੀ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ।
ਲੁਕੇ ਅਯਾਮਾਂ ਦਾ ਅਸਰ
[ਸੋਧੋ]ਕਿਸੇ ਵੀ ਹਾਲਤ ਵਿੱਚ, ਛੁਪੇ ਅਯਾਮ ਵਿੱਚ ਕਾਰਵਾਈ ਕਰਦੀ ਗਰੈਵਟੀ ਹੋਰ ਗੈਰ-ਗਰੈਵੀਟੇਸ਼ਨਲ ਬਲਾਂ ਤੇ ਪ੍ਰਭਾਵ ਪਾਉਂਦੀ ਹੈ ਜਿਵੇਂ ਬਿਜਲਈ-ਚੁੰਬਕਤਾ| ਅਸਲ ਵਿੱਚ, ਕਲੂਜਾ ਦੇ ਸ਼ੁਰੂਆਤੀ ਕੰਮ ਨੇ ਦਿਖਾਇਆ ਕਿ 5 ਅਯਾਮਾਂ ਵਿੱਚ ਜਨਰਲ ਰਿਲੇਟੀਵਿਟੀ ਅਸਲ ਵਿੱਚ ਬਿਜਲਈ- ਚੁੰਬਕਤਾ ਦੀ ਹੋਂਦ ਦਰਸਾਉਂਦੀ ਹੈ। ਫੇਰ ਵੀ, ਕਲਾਬੀ-ਯੂ ਬਹੁ-ਪਰਤਾਂ ਦੇ ਸੁਭਾਅ ਕਾਰਨ, ਸੂਖਮ ਅਯਾਮਾਂ ਤੋਂ ਕੋਈ ਨਵਾਂ ਬਲ ਨਹੀਂ ਦਿਸਦਾ, ਪਰ ਉਹਨਾਂ ਦਾ ਅਕਾਰ ਇਸ ਗੱਲ ਤੇ ਜੋਰਦਾਰ ਪ੍ਰਭਾਵ ਪਾਉਂਦਾ ਹੈ ਕਿ ਸਾਡੇ 4-ਅਯਾਮੀ ਬ੍ਰਹਿਮੰਡ ਵਿੱਚ ਸਟਰਿੰਗਾਂ ਦਰਮਿਆਨ ਬਲ ਕਿਵੇਂ ਦਿਸਦੇ ਹਨ। ਸਿਧਾਂਤ ਵਿੱਚ, ਫੇਰ ਵੀ, ਸਟੈਂਡਰਡ ਮਾਡਲ ਨਾਲ ਮਿਲਾਪ ਦੀ ਜਰੂਰਤ ਸਮਝ ਕੇ ਉਹਨਾਂ ਵਾਧੂ ਅਯਾਮਾਂ ਦੇ ਸੁਭਾਅ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨਾ ਸੰਭਵ ਹੈ, ਪਰ ਇਹ ਅਜੇ ਪ੍ਰੈਕਟੀਕਲ ਸੰਭਾਵਨਾ ਨਹੀਂ ਬਣ ਸਕਿਆ। ਗਰੈਵਟੀ ਦੇ ਸ਼ੁੱਧ ਟੈਸਟਾਂ ਰਾਹੀਂ ਛੁਪੇ ਅਯਾਮਾਂ ਨਾਲ ਸਬੰਧਤ ਸ਼ੁੱਧ ਸੂਚਨਾ ਪ੍ਰਾਪਤ ਕਰਨਾ ਵੀ ਸੰਭਵ ਹੈ, ਪਰ ਅਜੇ ਤੱਕ ਇਹਨਾਂ ਟੈਸਟਾਂ ਨੇ ਅਜਿਹੇ ਸੂਖਮ ਅਯਾਮਾਂ ਦੀ ਉੱਪਰਲੀ ਹੱਦ ਹੀ ਬੰਨੀ ਹੈ।
ਪਰਖ-ਯੋਗਤਾਵਾਂ ਅਤੇ ਪ੍ਰਯੋਗੀ ਭਵਿੱਖਬਾਣੀਆਂ
[ਸੋਧੋ]ਬੇਸ਼ਕ ਤਾਜਾ ਵਿਗਿਆਨਕ ਕੰਮ ਜਿਆਦਾਤਰ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦਾ ਇਸਤੇਮਾਲ ਪਾਰਟੀਕਲ ਫਿਜਿਕਸ ਦੇ ਵਾਸਤਿਬਿਕ ਮਾਡਲ ਬਣਾਉਣ ਲਈ ਧਿਆਨ ਦਿੰਦੇ ਰਹੇ ਹਨ, ਫੇਰ ਵੀ ਕਈ ਪ੍ਰਮੁੱਖ ਮੁਸ਼ਕਲਾਂ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੇ ਅਧਾਰ ਤੇ ਮਾਡਲਾਂ ਨੂੰ ਪਰਖਣਾ ਮੁਸ਼ਕਲ ਕਰਦੀਆਂ ਹਨ। ਸਭ ਤੋਂ ਜਿਆਦਾ ਮਹਤੱਵਪੂਰਨ ਪਲੈਂਕ ਲੈਂਥ ਦਾ ਸੂਖਮ ਅਕਾਰ ਹੈ, ਜੋ ਸਟਰਿੰਗ ਦੀ ਲੰਬਾਈ ਦੇ ਨੇੜੇ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ (ਇੱਕ ਸਟਰਿੰਗ ਦਾ ਵਿਸ਼ੇਸ਼ ਅਕਾਰ, ਜਿੱਥੇ ਸਟਰਿੰਗ ਕਣਾਂ ਨਾਲੋਂ ਅਸਾਨੀ ਨਾਲ ਵੱਖਰੇ ਹੋ ਜਾਂਦੇ ਹਨ)| ਇੱਕ ਹੋਰ ਮਸਲਾ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੇ ਪ੍ਰਮਾਣੂਆਂ ਦਾ ਖਾਲੀਪਣ ਹੈ, ਜੋ ਜਰੂਰ ਹੀ ਵੱਖਰੇ ਤੌਰ ਤੇ ਲੱਗਭੱਗ ਹਰੇਕ ਘਟਨਾ ਨੂੰ ਅਨੁਕੂਲ ਕਰਦਾ ਹੈ ਜੋ ਅਸੀਂ ਨੀਵੀਆਂ ਊਰਜਾਵਾਂ ਤੇ ਦੇਖਦੇ ਹਾਂ।
ਸਟਰਿੰਗ ਹਾਰਮੋਨਿਕਸ (String harmonics)
[ਸੋਧੋ]ਸਟਰਿੰਗ ਥਿਊਰੀ ਦਾ ਇੱਕ ਨਿਰਾਲਾ ਅਨੁਮਾਨ ਸਟਰਿੰਗ ਹਾਰਮੋਨਿਕਸ ਦੀ ਹੋਂਦ ਹੈ। ਜਰੂਰਤ ਮੁਤਾਬਿਕ ਉੱਚ ਉਰਜਾਵਾਂ ਤੇ, ਕਣਾਂ ਦਾ ਸਟਰਿੰਗ ਵਰਗਾ ਸੁਭਾਅ ਸਪਸ਼ੱਟ ਹੋ ਜਾਂਦਾ ਹੈ। ਸਟਰਿੰਗ ਦੇ ਉੱਚ ਆਵਰਤੀ ਵਾਲੇ ਹਾਰਮੋਨਿਕਸ ਨਾਲ ਸਬੰਧਿਤ, ਸਾਰੇ ਕਣਾਂ ਦੀਆਂ ਭਾਰੀਆਂ ਨਕਲਾਂ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ। ਇਹ ਸਪੱਸ਼ਟ ਨਹੀਂ ਹੈ ਇਹ ਊਰਜਾਵਾਂ ਕਿਵੇਂ ਹੁੰਦੀਆਂ ਹਨ। ਸਭ ਤੋਂ ਜਿਆਦਾ ਪ੍ਰੰਪਰਾਗਤ ਸਟਰਿੰਗ ਮਾਡਲਾਂ ਵਿੱਚ, ਇਹ ਪਲੈਂਕ ਊਰਜਾ ਦੇ ਨੇੜੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ, ਜੋ ਨਵੀਨ ਪਾਰਟੀਕਲ ਐਕਸੀਲੇਟਰ, LHC ਵਿੱਚ ਕ੍ਰਿਆਸ਼ੀਲ ਹੋਣ ਯੋਗ ਊਰਜਾਵਾਂ ਤੋਂ 1014 ਗੁਣਾ ਜਿਆਦਾ ਹੈ, ਤੇ ਸਾਨੂੰ ਨੇੜੇ ਭਵਿੱਖ ਵਿੱਚ ਕਿਸੇ ਪਾਰਟੀਕਲ ਐਕਸੀਲੇਟਰ ਨਾਲ ਇਸ ਅਨੁਮਾਨ ਨੂੰ ਪਰਖਣਾ ਅਸੰਭਵ ਕਰਦੀਆਂ ਹਨ। ਫੇਰ ਵੀ, ਵਿਸ਼ਾਲ ਵਾਧੂ ਅਯਾਮਾਂ ਨਾਲ ਇਹ ਸੰਭਵ ਤੌਰ ਤੇ LHC ਵਿੱਚ ਪੈਦਾ ਕੀਤੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ, ਜਾਂ ਇਸਦੀ ਪਹੁੰਚ ਦੇ ਅੰਦਰ ਦੀਆਂ ਊਰਜਾਵਾਂ ਤੇ ਪੈਦਾ ਕੀਤੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ।
ਫੀਨੋਮੀਨੌਲੌਜੀ
[ਸੋਧੋ]ਇੱਕ ਸਿਧਾਂਤਕ ਦਿਲਚਸਪੀ ਦਾ ਵਿਚਾਰਯੋਗ ਵਿਚਾਰ ਹੋਣ ਦੇ ਨਾਲ ਨਾਲ, ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਾਸਤਵਿਕ ਸੰਸਾਰ ਭੌਤਿਕ ਵਿਗਿਆਨ ਦੇ ਮਾਡਲ ਰਚਣ ਲਈ ਢਾਂਚਾ ਮੁਹੱਈਆ ਕਰਵਾਉਂਦੀ ਹੈ ਜੋ ਜਨਰਲ ਰਿਲੇਟੀਵਿਟੀ ਅਤੇ ਪਾਰਟੀਕਲ ਫਿਜ਼ਿਕਸ ਦਾ ਮੇਲ ਕਰਦਾ ਹੈ। ਫੀਨੋਮੀਨੌਲੌਜੀ ਸਿਧਾਂਤਕ ਭੌਤਿਕ ਵਿਗਿਆਨ ਦੀ ਓਹ ਸ਼ਾਖਾ ਹੈ ਜਿਸ ਵਿੱਚ ਭੌਤਿਕ ਵਿਗਿਆਨੀ ਹੋ ਜਿਆਦਾ ਸੰਖੇਪ ਸਿਧਾਂਤਕ ਵਿਚਾਰਾਂ ਤੋਂ ਕੁਦਰਤ ਦੇ ਵਾਸਤਵਿਕ ਮਾਡਲ ਰਚਦੇ ਹਨ । ਸਟਰਿੰਗ ਫੀਨੋਮੀਨੌਲੌਜੀ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦਾ ਅਜਿਹਾ ਹਿੱਸਾ ਹੈ ਜੋ ਸਟਰਿੰਗ ਥਿਊਰੀ ਉੱਤੇ ਅਧਾਰਿਤ ਵਾਸਤਵਿਕ ਮਾਡਲ ਰਚਣ ਦਾ ਯਤਨ ਕਰਦਾ ਹੈ।
ਕੁੱਝ ਸਿਧਾਂਤਕ ਅਤੇ ਗਣਿਤਿਕ ਸਮੱਸਿਆਵਾਂ ਕਾਰਣ, ਅਤੇ ਕੁੱਝ ਇਹਨਾਂ ਥਿਊਰੀਆਂ ਨੂੰ ਪ੍ਰਯੋਗਿਕ ਤੌਰ ਤੇ ਟੈਸਟ ਕਰਨ ਲਈ ਅਤਿ ਉੱਚ ਊਰਜਾਵਾਂ ਦੀ ਜਰੂਰਤ ਹੋਣ ਕਰਕੇ, ਹੁਣ ਤੱਕ ਕੋਈ ਪ੍ਰਯੋਗਿਕ ਸਬੂਤ ਉਪਲਬਧ ਨਹੀਂ ਹੈ ਜੋ ਸਪਸ਼ੱਟ ਰੂਪ ਵਿੱਚ ਇਸ਼ਾਰਾ ਕਰ ਸਕੇ ਕਿ ਇਹਨਾਂ ਮਾਡਲਾਂ ਵਿੱਚੋਂ ਕੋਈ ਵੀ ਮਾਡਲ ਕੁਦਰਤ ਦੇ ਵਿਵਰਣ ਦਾ ਸਹੀ ਮੁਢਲਾ ਵਿਵਰਣ ਹੈ। ਇਸ ਗੱਲ ਨੇ ਵਿਗਿਆਨਿਕ ਸਮਾਜ ਅੰਦਰ ਕੁੱਝ ਨੂੰ ਏਕੀਕਰਨ ਪ੍ਰਤਿ ਇਹਨਾਂ ਪਹੁੰਚਾਂ ਦੀ ਅਲੋਚਨਾ ਕਰਨ ਦਾ ਮੌਕਾ ਦਿੱਤਾ ਹੈ ਅਤੇ ਇਹਨਾਂ ਕਠਿਨਾਈਆਂ ਉੱਤੇ ਨਿਰੰਤਰ ਖੋਜ ਦੀ ਕੀਮਤ ਉੱਤੇ ਸਵਾਲ ਕਰਨ ਲਈ ਮਜਬੂਰ ਕੀਤਾ ਹੈ।
ਬ੍ਰਹਿਮੰਡ ਵਿਗਿਆਨ (Cosmology)
[ਸੋਧੋ]ਅੱਜਕੱਲ ਦੀ ਸਮਝ ਮੁਤਾਬਕ ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿਸ਼ਾਲ ਪੱਧਰ ਤੇ ਬ੍ਰਹਿਮੰਡ ਦੀ ਬਣਤਰ ਬਾਰੇ ਅਨੁਮਾਨਾਂ ਦੀ ਲੜੀ ਬਣਾਉਂਦੀ ਹੈ। ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ ਕਈ ਹਾਲਤਾਂ ਵਿੱਚ ਵਿਸ਼ਾਲ ਪੌਜੇਟਿਵ ਵੈਕੱਮ ਊਰਜਾ (ਵਾਸਤਵਿਕ ਕਣਾਂ ਦੇ ਜੋੜਿਆਂ ਦੇ ਜੁੜ ਕੇ ਟੁੱਟਣ ਨਾਲ ਪੈਦਾ ਹੋਈ ਊਰਜਾ) ਹੈ। ਬ੍ਰਹਿਮੰਡ ਦੇ ਅਜਿਹੀ ਅਵਸਥਾ ਵਾਲੇ ਖੇਤਰ ਚਿਰਸਥਾਈ ਫੈਲਾਓ ਨਾਮਕ ਕ੍ਰਿਆ ਨਾਲ ਤੇਜੀ ਨਾਲ ਫੈਲਦੇ ਹਨ। ਇਵੇਂ ਹੀ, ਥਿਊਰੀ ਅਨੁਮਾਨ ਲਗਾਉਂਦੀ ਹੈ ਕਿ ਬ੍ਰਹਿਮੰਡ ਦਾ ਜਿਆਦਾਤਰ ਹਿੱਸਾ ਤੇਜੀ ਨਾਲ ਫੈਲ ਰਿਹਾ ਹੈ। ਫੇਰ ਵੀ, ਇਹ ਫੈਲ ਰਹੀਆਂ ਅਵਸਥਾਵਾਂ ਸਥਾਈ ਨਹੀਂ ਹਨ, ਅਤੇ ਨੀਵੀਂ ਵੈਕੱਮ ਊਰਜਾ ਦੇ ਬੁਲਬੁਲਿਆਂ ਦੀ ਨਿਊਕਲੀਏਸ਼ਨ ਰਾਹੀਂ ਲੀਕ ਹੋ ਸਕਦੀ ਹੈ। ਕਿਉਂਕਿ ਬ੍ਰਹਿਮੰਡ ਦਾ ਸਾਡਾ ਸਥਾਨਿਕ ਖੇਤਰ ਤੇਜੀ ਨਾਲ ਫੈਲ ਨਹੀਂ ਰਿਹਾ, ਸਟਰਿੰਗ ਥਿਊਰੀ ਅਨੁਮਾਨ ਲਗਾਉਂਦੀ ਹੈ ਕਿ ਅਸੀਂ ਅਜਿਹੇ ਬੁਲਬਲੇ ਦੇ ਅੰਦਰ ਹਾਂ| ਬੁਲਬੁਲਿਆਂ ਦੇ ਅੰਦਰ ਦੀ ਬ੍ਰਹਿਮੰਡ ਦੀ ਸਥਾਨਿਕ ਗੋਲਾਈ ਜੋ ਇੱਕ ਪਰਖਯੋਗ ਅਨੁਮਾਨ ਹੈ ਤੇ ਇਸ ਕ੍ਰਿਆ ਦੁਆਰਾ ਬਣਦੀ ਹੈ, ਨੈਗੇਟਿਵ ਹੁੰਦੀ ਹੈ। ਹੋਰ ਅੱਗੇ, ਬੁਲਬੁਲੇ ਅੰਤ ਨੂੰ ਬੁਲਬੁਲਿਆਂ ਦੇ ਬਾਹਰ ਮੁੱਖ ਵੈਕੱਮ ਦਾ ਨਿਰਮਾਣ ਕਰਦੇ ਹਨ ਤੇ ਇਸ ਨਾਲ ਟਕਰਾਉਂਦੇ ਹਨ। ਇਹ ਟਕਰਾਓ ਸੰਭਵ ਤੌਰ ਤੇ ਬ੍ਰਹਿਮੰਡ ਵਿਗਿਆਨ ਵਿੱਚ ਦਿਸਣਯੋਗ ਨੋਸ਼ਾਨ ਛੱਡਦੇ ਹਨ। ਫੇਰ ਵੀ, ਇਹ ਸੰਭਵ ਹੈ ਕਿ ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਵੀ ਦੇਖਿਆ ਨਹੀਂ ਜਾ ਸਕੇਗਾ ਜੇਕਰ ਸਥਾਨਿਕ ਗੋਲਾਈ ਬਹੁਤ ਸੂਖਮ ਹੋਵੇਗੀ ਅਤੇ ਟਕਰਾਓ ਬਹੁਤ ਘੱਟ ਹੋਣਗੇ|
ਕੁੱਝ ਹਾਲਤਾਂ ਵਿੱਚ, ਫੈਲਾਓ ਦੇ ਅੰਤ ਦੇ ਨੇੜੇ ਪੈਦਾ ਹੋਏ ਮੁਢਲੇ ਸਟਰਿੰਗ ਖਗੋਲਿਕ ਅਨੁਪਾਤਾਂ ਤੱਕ ਖਿੱਚੇ ਜਾ ਸਕਦੇ ਹਨ। ਇਹ ਬ੍ਰਹਿਮੰਡੀ ਸਟਰਿੰਗ ਕਈ ਤਰੀਕਿਆਂ ਨਾਲ ਦੇਖੇ ਜਾ ਸਕਦੇ ਹਨ, ਜਿਵੇਂ ਉਹਨਾਂ ਦੇ ਗਰੂਤਾਕਰਸ਼ਣ ਲੈਂਸਿੰਗ ਪ੍ਰਭਾਵਾਂ ਰਾਹੀਂ|( ਗਰੂਤਾਕੇਸ਼ਣ ਲੈਂਸਿੰਗ= ਦੂਰ ਦੇ ਸੋਮੇ ਅਤੇ ਦਰਸ਼ਕ ਵਿਚਕਾਰ ਗਲੈਕਸੀਆਂ ਦੇ ਝੁੰਡਾਂ ਦੀਆਂ ਪਲੇਟਾਂ ਦੀ ਵੰਡ)| ਫੇਰ ਵੀ, ਕੁੱਝ ਫੀਲਡ ਥਿਊਰੀਆਂ ਇਹ ਅਨੁਮਾਨ ਵੀ ਲਗਾਉਂਦੀਆਂ ਹਨ ਕਿ ਬ੍ਰਹਿਮੰਡੀ ਸਟਰਿੰਗ ਫੀਲਡ ਬਣਤਰਾਂ ਵਿੱਚ ਸਮਸਥਾਨਿਕ (topological) ਨੁਕਸਾਂ ਤੋਂ ਪੈਦਾ ਹੁੰਦੇ ਹਨ।
ਸੁੱਪਰ ਸਮਰੂਪਤਾ (Supersymmetry)
[ਸੋਧੋ]ਜੇਕਰ ਪ੍ਰਯੋਗਿਕ ਤੌਰ ਤੇ ਸਾਬਤ ਹੋ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਸੁਪਰਸਮਰੂਪਤਾ ਵੀ ਸੰਯੋਗਵਸ਼ ਗਵਾਹ ਦੇ ਤੌਰ ਤੇ ਲਈ ਜਾ ਸਕਦੀ ਹੈ, ਕਿਉਂਕਿ ਸਾਰੀਆਂ ਸਥਾਈ ਸਟਰਿੰਗ ਥਿਊਰੀਆਂ ਸੁਪਰਸਮਰੂਪ ਹਨ। ਫੇਰ ਵੀ, ਵਿਸ਼ਾਲ ਹਾਡਰਨ ਕੋਲਾਈਡਰ LHC ਵਿੱਚ ਕ੍ਰਿਆਯੋਗ ਊਰਜਾਵਾਂ ਤੇ ਸੁਪਰਸਮਰੂਪ ਕਣਾਂ ਦੀ ਗੈਰਹਾਜ਼ਰੀ ਜਰੂਰੀ ਨਹੀਂ ਹੈ ਕਿ ਸਟਰਿੰਗ ਥਿਊਰੀ ਨੂੰ ਸਾਬਤ ਨਾ ਕਰੇ, ਕਿਉਂਕਿ ਜਿਸ ਊਰਜਾ ਪੈਮਾਨੇ ਤੇ ਸੁਪਰਸਮਰੂਪਤਾ ਟੁੱਟ ਜਾਂਦੀ ਹੈ ਉਹ ਚੰਗੀ ਤਰਾਂ ਐਕਸਲਰੇਟਰ ਦੇ ਦਾਇਰੇ ਤੋਂ ਉੱਪਰ ਹੋ ਸਕਦਾ ਹੈ।
AdS/CFT ਮੇਲ
[ਸੋਧੋ]anti-de Sitter/conformal field theory (AdS/CFT) ਮੇਲ ਇੱਕ ਸਬੰਧ ਹੈ ਜਿਸਦੇ ਮੁਤਾਬਿਕ ਕੁੱਝ ਹਾਲਤਾਂ ਵਿੱਚ ਸਟਰਿੰਗ ਥਿਊਰੀ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਬਰਾਬਰ ਹੈ। ਜਿਆਦਾ ਸੰਖੇਪ ਵਿੱਚ ਕਹਿੰਦੇ ਹੋਏ, ਸਟਰਿੰਗ ਥਿਊਰੀ ਜਾਂ ਐੱਮ-ਥਿਊਰੀ ਨੂੰ ਇੱਕ anti-de Sitter ਪਿਛੋਕੜ ਤੇ ਦੇਖਣਾ ਹੈ। ਇਸਦਾ ਅਰਥ ਹੈ ਕਿ ਪੁਲਾੜ ਵਿੱਚ ਆਈਨਸਟਾਈਨ ਦੀ ਸਮੀਕਰਨ ਦੇ ਕੁੱਝ ਹੱਲਾਂ ਨੂੰ ਵਿਗਾੜ ਕੇ ਸਪੇਸਸਮੇਂ ਦਾ ਰੇਖਾ ਗਣਿਤ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ। ਇਸ ਸੈੱਟਿੰਗ ਵਿੱਚ, ਸਪੇਸ ਸਮੇਂ ਦੀ ਹੱਦ ਪਰਿਭਾਸ਼ਿਤ ਕਰਨੀ ਸੰਭਵ ਹੈ। AdS/CFT ਮੇਲ ਦਰਸਾਉਂਦਾ ਹੈ ਕਿ ਇੱਕ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਲਈ ਇਸ ਹੱਦ ਨੂੰ ਸਪੇਸ ਸਮਾਂ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ, ਅਤੇ ਇਹ ਫੀਲਡ ਥਿਊਰ ਵਿਸ਼ਾਲ ਗਰੂਕਾਰਸ਼ਨ ਥਿਊਰੀ ਦੇ ਨਾਲ ਉਸ ਸਮਝ ਅਨੁਸਾਰ ਬਰਾਬਰ ਹੈ ਜਿਸ ਵਿੱਚ, ਇੱਕ ਥਿਊਰੀ ਦੇ ਹਿਸਾਬ ਕਿਤਾਬ ਨੂੰ ਦੂਜੀ ਥਿਊਰੀ ਦੇ ਹਿਸਾਬ ਕਿਤਾਬ ਵਿੱਚ ਅਨੁਵਾਦ ਕਰਨ ਦਾ ਸ਼ਬਦਕੋਸ਼ ਹੋਵੇ|
ਮੇਲ ਦੀਆਂ ਉਦਾਹਰਨਾਂ
[ਸੋਧੋ]AdS/CFT ਮੇਲ ਦੀ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਉਦਾਹਰਨ ਮੁਤਾਬਿਕ Type IIB ਸਟਰਿੰਗ ਥਿਊਰੀ AdS5 × S5 ਦੀ ਪੈਦਾਵਰ ਤੇ 4-ਅਯਾਮੀ ਅਨੁਰੂਪ ਹੱਦ ਤੇ N = 4 super Yang–Mills ਥਿਊਰੀ ਬਰਾਬਰ ਹੈ। ਇਸ ਮੇਲ ਦੇ ਇੱਕ ਹੋਰ ਅਨੁਭਵ ਅਨੁਸਾਰ AdS4 × S7 ਉੱਤੇ ਐੱਮ-ਥਿਊਰੀ 3-ਅਯਾਮਾਂ ਵਿੱਚ ABJM superconformal ਫੀਲਡ ਥਿਊਰੀ ਬਰਾਬਰ ਹੈ। ਅਜੇ ਇੱਕ ਹੋਰ ਅਨੁਭਵ ਅਨੁਸਾਰ AdS7 × S4 ਉੱਤੇ ਐੱਮ-ਥਿਊਰੀ 6-ਅਯਾਮਾਂ ਵਿੱਚ (2,0)-ਥਿਊਰੀ ਬਰਾਬਰ ਹੈ।
ਕੁਆਂਟਮ ਕਰੋਮੋਡਾਇਨਾਮਿਕਸ ਲਈ ਇਸਤੇਮਾਲ
[ਸੋਧੋ]ਕਿਉਂਕਿ ਇਹ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦਾ ਸਧਾਰਨ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਨਾਲ ਮੇਲ ਕਰਦਾ ਹੈ, AdS/CFT ਮੇਲ ਨੂੰ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਵਿੱਚ ਹਿਸਾਬ ਲਗਾਉਣ ਲਈ ਸਿਧਾਂਤਕ ਔਜਾਰ ਦੇ ਤੌਰ ਤੇ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਉਦਾਹਰਨ ਵਜੋਂ, ਇਸ ਮੇਲ ਨੂੰ ਕੁਆਰਕ-ਗਲੂਔਨ ਪਲਾਜ਼ਮਾ ਦੇ ਅਧਿਐਨ ਲਈ ਵਰਤਿਆ ਗਿਆ ਹੈ, ਜੋ ਪਾਰਟੀਕਲ ਐਕਸੀਲੇਟਰ ਵਿੱਚ ਪੈਦਾ ਹੋਏ ਪਦਾਰਥ ਦੀ ਅਜੀਬ ਅਵਸਥਾ ਹੈ।
ਕੁਆਰਕ-ਗਲੂਔਨ ਪਲਾਜ਼ਮਾ ਦੀ ਭੌਤਿਕ ਵਿਗਿਆਨ ਕੁਆਂਟਮ ਕਰੋਮੋਡਾਇਨਾਮਿਕਸ ਰਾਹੀਂ ਚਲਾਈ ਜਾਂਦੀ ਹੈ, ਜੋ ਤਾਕਤਵਰ ਨਿਊਕਲੀਅਰ ਬਲ ਦੀ ਮੁਢਲੀ ਥਿਊਰੀ ਹੈ, ਪਰ ਇਹ ਥਿਊਰੀ ਕੁਆਰਕ-ਗਲੂਔਨ ਪਲਾਜ਼ਮਾ ਦੇ ਮਾਮਲੇ ਵਿੱਚ ਗਣਿਤਿਕ ਤੌਰ ਤੇ ਸਮੱਸਿਆਵਾਂ ਰਾਹੀਂ ਸਹੀ ਨਹੀਂ ਬੈਠਦੀ| ਕੁਆਰਕ-ਗਲੂਔਨ ਪਲਾਜ਼ਮਾ ਦੀਆਂ ਕੁੱਝ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਨੂੰ ਸਮਝਣ ਲਈ, ਸਿਧਾਂਤਵਾਦੀਆਂ ਨੇ ਇਸਲਈ AdS/CFT ਮੇਲ ਦੀ ਵਰਤੋ ਕੀਤੀ ਹੈ। ਇਸ ਮੇਲ ਦਾ ਇੱਕ ਰੂਪ ਸਟਰਿੰਗ ਥਿਊਰੀ ਨੂੰ ਇੱਕ ਨਿਸ਼ਚਿਤ ਸੁਪਰਸਮਰੂਪ ਗੇਜ਼ ਥਿਊਰੀ ਨਾਲ ਮਿਲਾਉਂਦਾ ਹੈ ਜਿਸ ਨੂੰ N = 4 super Yang–Mills theory ਕਹਿੰਦੇ ਹਨ। ਬਾਦ ਵਿੱਚ ਲਿਖੀ ਥਿਊਰੀ ਕੁਆਂਟਮ ਕਰੋਮੋਡਾਇਨਾਮਿਕਸ ਲਈ ਲੱਗਭੱਗ ਚੰਗੀ ਸਮਾਨਤਾ ਮੋਹੱਈਆ ਕਰਵਾਉਂਦੀ ਹੈ। ਕੋਈ ਵੀ ਇਸਤਰਾਂ ਕੁਆਰਕ-ਗਲੂਔਨ ਪਲਾਜ਼ਮਾ ਨਾਲ ਸਬੰਧਿਤ ਸਮੱਸਿਆਵਾਂ ਨੂੰ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ ਵਿੱਚ ਬਦਲ ਸਕਦਾ ਹੈ ਜੋ ਜਿਆਦਾ ਅਸਾਨ ਹਨ। ਇਹ ਤਰੀਕੇ ਵਰਤਦੇ ਹੋਏ, ਸਿਧਾਂਤਵਾਦੀਆਂ ਨੇ ਕੁਆਰਕ-ਗਲੂਔਨ ਪਲਾਜ਼ਮਾ ਦਾ ਕੱਟਿਆ ਹੋਇਆ ਦਲਦਲਪੁਣਾ (shear viscosity) ਮਿਣਿਆ ਹੈ। 2008 ਵਿੱਚ, ਬਰੁੱਕਹੈਵਨ ਰਾਸ਼ਟਰੀ ਪ੍ਰਯੋਗਸ਼ਾਲਾ (Brookhaven National Laboratory) ਵਿੱਚ ਤੁਲਨਾਤਮਕ ਭਾਰੀ ਆਇਔਨ ਕੋਲਾਈਡਰ (Relativistic Heavy Ion Collider) ਤੇ ਇਹ ਅਨੁਮਾਨ ਸਾਬਤ ਕੀਤੇ ਗਏ ਹਨ।
ਸੰਘਣੇ ਪਦਾਰਥ ਵਾਲੀ ਭੌਤਿਕ ਵਿਗਿਆਨ ਲਈ ਇਸਤੇਮਾਲ
[ਸੋਧੋ]ਇਸਦੇ ਨਾਲ ਨਾਲ, ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੇ ਤਰੀਕੇ ਸੰਘਣੇ ਪਦਾਰਥ ਦੀ ਭੌਤਿਕ ਵਿਗਿਆਨ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ ਤੇ ਵੀ ਲਾਗੂ ਕੀਤੇ ਗਏ ਹਨ। ਕੁੱਝ ਸੰਘਣੇ ਪਦਾਰਥ ਦੀਆਂ ਪ੍ਰਣਾਲੀਆਂ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਦੇ ਤਰੀਕਿਆਂ ਦੀ ਵਰਤੋਂ ਨਾਲ ਸਮਝਣੀਆਂ ਮੁਸ਼ਕਲ ਹਨ, ਅਤੇ AdS/CFT ਮੇਲ ਭੌਤਿਕ ਵਿਗਿਆਨੀਆਂ ਨੂੰ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੀ ਭਾਸ਼ਾ ਵਿੱਚ ਇਹਨਾਂ ਪ੍ਰਣਾਲੀਆਂ ਨੂੰ ਚੰਗੀ ਤਰਾਂ ਸਮਝਣ ਦੀ ਅਗਿਆ ਦਿੰਦਾ ਹੈ। ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੇ ਤਰੀਕਿਆਂ ਰਾਹੀਂ ਇੱਕ ਸੁਪਰਫਲੱਡ ਦੀ ਇੱਕ ਇਨਸੁਲੇਟਰ ਵਿੱਚ ਤਬਦੀਲੀ ਦੀ ਵਿਆਖਿਆ ਰਾਹੀਂ ਕਾਫੀ ਸਫਲਤਾ ਹਾਸਲ ਹੋਈ ਹੈ।
ਗਣਿਤ ਨਾਲ ਸਬੰਧ
[ਸੋਧੋ]ਸਿਧਾਂਤਕ ਭੌਤਿਕ ਵਿਗਿਆਨ ਦੀਆਂ ਪ੍ਰਭਾਵਸ਼ਾਲੀ ਖੋਜਾਂ ਵਿੱਚ ਹੋਰ ਜੋੜਦੇ ਹੋਏ, ਸਟਰਿੰਗ ਥਿਊਰੀ ਨੇ ਸੁੱਧ-ਗਣਿਤ ਦੇ ਵਿੱਚ ਬਹੁਤ ਸਾਰਾ ਵਿਕਾਸ ਕੀਤਾ ਹੈ। ਸਿਧਾਂਤਕ ਭੌਤਿਕ ਵਿਗਿਆਨ ਦੇ ਵਿਕਸਿਤ ਹੋ ਰਹੇ ਵਿਚਾਰਾਂ ਵਾਂਗ, ਸਟਰਿੰਗ ਥਿਊਰੀ ਕੋਲ ਫਿਲਹਾਲ ਕਠੋਰ ਗਣਿਤਿਕ ਬਣਤਰਾਂ ਨਹੀਂ ਹਨ ਜਿਸ ਵਿੱਚ ਇਸਦੇ ਸਾਰੇ ਸੰਕਲਪ ਸੰਖੇਪ ਰੂਪ ਵਿੱਚ ਦਰਸਾਏ ਜਾ ਸਕਣ। ਨਤੀਜੇ ਵਜੋਂ, ਜੋ ਭੌਤਿਕ ਵਿਗਿਆਨੀ ਸਟਰਿੰਗ ਥਿਊਰੀ ਦਾ ਅਧਿਐਨ ਕਰਦੇ ਹਨ,ਅਕਸਰ ਦਿਸਦੀਆਂ ਵਿਭਿੰਨ ਗਣਿਤਿਕ ਢਾਂਚਿਆਂ ਦਰਮਿਆਨ ਸਬੰਧਾਂ ਦਾ ਅਨੁਮਾਨ ਲਾਉਣ ਲਈ ਭੌਤਿਕੀ ਸਹਿਜ-ਗਿਆਨ ਦੁਆਰਾ ਹੀ ਗਾਈਡ ਕੀਤੇ ਜਾਂਦੇ ਹਨ ਜੋ ਥਿਊਰੀ ਦੇ ਵੱਖਰੇ ਹਿੱਸਿਆਂ ਦੀ ਬਣਤਰ ਲਈ ਵਰਤੇ ਜਾਂਦੇ ਹਨ। ਇਹ ਅਨੁਮਾਨ ਬਾਦ ਵਿੱਚ ਗਣਿਤਸ਼ਾਸਤਰੀਆਂ ਦੁਆਰਾ ਸਾਬਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ, ਅਤੇ ਇਸ ਤਰਾਂ, ਸਟ੍ਰਿੰਗ ਥਿਊਰੀ ਨੇ ਸ਼ੁੱਧ ਗਣਿਤ ਵਿੱਚ ਨਵੇਂ ਵਿਚਾਰਾਂ ਦੇ ਸੋਮੇ ਦੇ ਰੂਪ ਵਿੱਚ ਕੰਮ ਕੀਤਾ ਹੈ।
ਦਰਪਣ ਸਮਰੂਪਤਾ (Mirror symmetry)
[ਸੋਧੋ]
ਦਰਪਣ ਸਮਰੂਪਤਾ ਦੀ ਖੋਜ ਰਾਹੀਂ ਸਟਰਿੰਗ ਥਿਊਰੀ ਨੇ ਗਣਿਤ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕੀਤਾ ਹੈ। ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ, ਅਦ੍ਰਿਸ਼ ਸਥਾਨਿਕ ਅਯਾਮਾਂ ਦਾ ਅਕਾਰ ਆਮ ਤੌਰ ਤੇ ਕਾਲਾਬਿ-ਯਾਊ ਬਹੁ-ਪਰਤਾਂ ਨਾਮਕ ਗਣਿਤਿਕ ਚੀਜਾਂ ਵਿੱਚ ਸੰਕੇਤਿਕ ਸ਼ਬਦਾਂ ਵਿੱਚ ਬਦਲਿਆ ਜਾਂਦਾ ਹੈ (encoded)| ਇਹ ਸ਼ੁੱਧ ਗਣਿਤ ਵਿੱਚ ਦਿਲਚਸਪੀ ਵਾਲੀਆਂ ਹਨ, ਤੇ ਸਟਰਿੰਗ ਥਿਊਰੀ ਰਾਹੀਂ ਫਿਜਿਕਸ ਦੇ ਯਥਾਰਥਵਾਦੀ ਮਾਡਲਾਂ ਦੀ ਬਣਤਰ ਲਈ ਵਰਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ। 1980ਵੇਂ ਦਹਾਕੇ ਦੇ ਅਖੀਰ ਵਿੱਚ, ਇਹ ਨੋਟ ਕੀਤਾ ਗਿਆ ਕਿ ਕਿਸੇ ਦਿੱਤੇ ਹੋਏ ਫਿਜਿਕਲ ਮਾਡਲ ਲਈ, ਸਬੰਧਿਤ ਨਿਰਾਲੀ ਕਾਲਾਬਿ-ਯਾਊ ਬਹੁ-ਪਰਤ ਬਣਾਉਣੀ ਸੰਭਵ ਹੈ। ਸਗੋਂ, ਇਹ ਵੀ ਖੋਜਿਆ ਗਿਆ ਕਿ ਦੋ ਕਾਲਾਬਿ-ਯਾਊ ਬਹੁ-ਪਰਤਾਂ ਇੱਜੋ ਫਿਜਿਕਸ ਬਣਾਉਂਦੀਆਂ ਹਨ। ਇਹਨਾਂ ਬਹੁ-ਪਰਤਾਂ ਨੂੰ ਇੱਕ ਦੂਜੀ ਦੀਆਂ ਦਰਪਣ ਕਿਹਾ ਗਿਆ| ਵਿਭਿੰਨ ਕਾਲਾਬਿ-ਯਾਊ ਬਹੁ-ਪਰਤਾਂ ਦਰਮਿਆਨ ਇਸ ਦਰਪਣ ਸਮਰੂਪਤਾ ਸਬੰਧ ਦੀ ਹੋਂਦ ਦੀਆਂ ਮਹੱਤਵਪੂਰਨ ਗਣਿਤਿਕ ਲੜੀਆਂ ਬਣਦੀਆਂ ਹਨ ਕਿਉਂਕਿ ਇਹ ਗਿਣਤੀ ਸੂਚਕ ਅਲਜਬਰਿਕ ਰੇਖਾਗਣਿਤ ਦੀਆਂ ਕਈ ਸਮੱਸਿਆਵਾਂ ਹੱਲ ਕਰਨ ਵਿੱਚ ਗਣਿਤਸ਼ਾਸਤਰੀਆਂ ਦੀ ਮਦੱਦ ਕਰਦਾ ਹੈ। ਅੱਜਕੱਲ ਗਣਿਤਸ਼ਾਸਤਰੀ ਅਜੇ ਵੀ ਭੌਤਿਕ ਵਿਗਿਆਨੀਆਂ ਦੇ ਸਹਿਜ ਗਿਆਨ ਤੇ ਅਧਾਰਿਤ ਦਰਪਣ ਸਮਰੂਪਤਾ ਦੀ ਗਣਿਤਿਕ ਸਮਝ ਵਿਕਸਿਤ ਕਰਨ ਵਿੱਚ ਲੱਗੇ ਹੋਏ ਹਨ।
ਸ਼ਿਖਰ ਅਪਰੇਟਰ ਬੀਜਗਣਿਤ (Vertex operator algebras)
[ਸੋਧੋ]ਦਰਪਣ ਸਮਰੂਪਤਾ ਤੋਂ ਇਲਾਵਾ, ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੇ ਸ਼ੁੱਧ ਗਣਿਤ ਵਿੱਚ ਉਪਯੋਗਾਂ ਵਿੱਚ ਸ਼ਿਖਰ ਅਪਰੇਟਰ ਬੀਜਗਣਿਤ (Vertex operator algebras) ਦੀ ਥਿਊਰੀ ਸ਼ਾਮਲ ਹੈ। ਉਦਾਹਰਨ ਵਜੋਂ, ਸਟਰਿੰਗ ਥਿਊਰੀ ਦੇ ਵਿਚਾਰ 1992 ਵਿੱਚ ਰਿਚਰਡ ਬੋਰਚਰਡਜ਼ ਦੁਆਰਾ monstrous moonshine ਅਨੁਮਾਨ ਨੂੰ ਸਾਬਤ ਕਰਨ ਵਰਤੇ ਗਏ ਜੋ monster group (ਗਰੁੱਪ ਥਿਊਰੀ ਵਿੱਚ ਪੈਦਾ ਹੋਈ ਇੱਕ ਬਣਤਰ)ਤੇ modular functions (ਨੰਬਰ ਥਿਊਰੀ ਵਿੱਚ ਮਹੱਤਵਪੂਰਨ ਫੰਕਸ਼ਨਾਂ ਦੀ ਇੱਕ ਸ਼੍ਰੇਣੀ) ਨਾਲ ਸਬੰਧਿਤ ਸੀ।
ਹਵਾਲੇ
[ਸੋਧੋ]ਨੋਟਸ
[ਸੋਧੋ]ਹੋਰ ਹਵਾਲੇ
[ਸੋਧੋ]ਸੰਦਰਭ ਗ੍ਰੰਥ ਸੂਚੀ
[ਸੋਧੋ]- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000011-QINU`"'</ref>" does not exist.
- Banks, Tom; Fischler, Willy; Schenker, Stephen; Susskind, Leonard (1997). "M theory as a matrix model: A conjecture". Physical Review D. 55 (8): 5112–5128. arXiv:hep-th/9610043. Bibcode:1997PhRvD..55.5112B. doi:10.1103/physrevd.55.5112.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000014-QINU`"'</ref>" does not exist.
- Bekenstein, Jacob (1973). "Black holes and entropy". Physical Review D. 7 (8): 2333–2346. Bibcode:1973PhRvD...7.2333B. doi:10.1103/PhysRevD.7.2333.
- Bergshoeff, Eric; Sezgin, Ergin; Townsend, Paul (1987). "Supermembranes and eleven-dimensional supergravity". Physics Letters B. 189 (1): 75–78. Bibcode:1987PhLB..189...75B. doi:10.1016/0370-2693(87)91272-X.
- Borcherds, Richard (1992). "Monstrous moonshine and Lie superalgebras". Inventiones Mathematicae. 109 (1): 405–444. Bibcode:1992InMat.109..405B. doi:10.1007/BF01232032.
- Candelas, Philip; de la Ossa, Xenia; Green, Paul; Parks, Linda (1991). "A pair of Calabi–Yau manifolds as an exactly soluble superconformal field theory". Nuclear Physics B. 359 (1): 21–74. Bibcode:1991NuPhB.359...21C. doi:10.1016/0550-3213(91)90292-6.
- Candelas, Philip; Horowitz, Gary; Strominger, Andrew; Witten, Edward (1985). "Vacuum configurations for superstrings". Nuclear Physics B. 258: 46–74. Bibcode:1985NuPhB.258...46C. doi:10.1016/0550-3213(85)90602-9.
- Castro, Alejandra; Maloney, Alexander; Strominger, Andrew (2010). "Hidden conformal symmetry of the Kerr black hole". Physical Review D. 82 (2). arXiv:1004.0996. Bibcode:2010PhRvD..82b4008C. doi:10.1103/PhysRevD.82.024008.
- Cheng, Miranda; Duncan, John; Harvey, Jeffrey (2013). "Umbral Moonshine". arXiv:1204.2779.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000001C-QINU`"'</ref>" does not exist.
- Connes, Alain; Douglas, Michael; Schwarz, Albert (1998). "Noncommutative geometry and matrix theory". Journal of High Energy Physics. 19981 (2): 003. arXiv:hep-th/9711162. Bibcode:1998JHEP...02..003C. doi:10.1088/1126-6708/1998/02/003.
- Conway, John; Norton, Simon (1979). "Monstrous moonshine". Bull. London Math. Soc. 11 (3): 308–339. doi:10.1112/blms/11.3.308.
- Cremmer, Eugene; Julia, Bernard; Scherk, Joel (1978). "Supergravity theory in eleven dimensions". Physics Letters B. 76 (4): 409–412. Bibcode:1978PhLB...76..409C. doi:10.1016/0370-2693(78)90894-8.
- de Haro, Sebastian; Dieks, Dennis; 't Hooft, Gerard; Verlinde, Erik (2013). "Forty Years of String Theory Reflecting on the Foundations". Foundations of Physics. 43 (1): 1–7. Bibcode:2013FoPh...43....1D. doi:10.1007/s10701-012-9691-3.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000021-QINU`"'</ref>" does not exist.
- Duff, Michael (1996). "M-theory (the theory formerly known as strings)". International Journal of Modern Physics A. 11 (32): 6523–41. arXiv:hep-th/9608117. Bibcode:1996IJMPA..11.5623D. doi:10.1142/S0217751X96002583.
- Duff, Michael (1998). "The theory formerly known as strings". Scientific American. 278 (2): 64–9. doi:10.1038/scientificamerican0298-64.
- Duff, Michael; Howe, Paul; Inami, Takeo; Stelle, Kellogg (1987). "Superstrings in D=10 from supermembranes in D=11". Nuclear Physics B. 191 (1): 70–74. Bibcode:1987PhLB..191...70D. doi:10.1016/0370-2693(87)91323-2.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000029-QINU`"'</ref>" does not exist.
- Duncan, John; Griffin, Michael; Ono, Ken (2015). "Proof of the Umbral Moonshine Conjecture". arXiv:1503.01472.
- Eguchi, Tohru; Ooguri, Hirosi; Tachikawa, Yuji (2011). "Notes on the K3 surface and the Mathieu group M24". Experimental Mathematics. 20 (1): 91–96. doi:10.1080/10586458.2011.544585.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000002E-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000002F-QINU`"'</ref>" does not exist.
- Givental, Alexander (1996). "Equivariant Gromov-Witten invariants". International Mathematics Research Notices. 1996 (13): 613–663. doi:10.1155/S1073792896000414.
{{cite journal}}: CS1 maint: unflagged free DOI (link) - Givental, Alexander (1998). "A mirror theorem for toric complete intersections". Topological field theory, primitive forms and related topics: 141–175. doi:10.1007/978-1-4612-0705-4_5. ISBN 978-1-4612-6874-1.
- Gubser, Steven; Klebanov, Igor; Polyakov, Alexander (1998). "Gauge theory correlators from non-critical string theory". Physics Letters B. 428: 105–114. arXiv:hep-th/9802109. Bibcode:1998PhLB..428..105G. doi:10.1016/S0370-2693(98)00377-3.
- Guica, Monica; Hartman, Thomas; Song, Wei; Strominger, Andrew (2009). "The Kerr/CFT Correspondence". Physical Review D. 80 (12). arXiv:0809.4266. Bibcode:2009PhRvD..80l4008G. doi:10.1103/PhysRevD.80.124008.
- Hawking, Stephen (1975). "Particle creation by black holes". Communications in Mathematical Physics. 43 (3): 199–220. Bibcode:1975CMaPh..43..199H. doi:10.1007/BF02345020.
- Hawking, Stephen (2005). "Information loss in black holes". Physical Review D. 72 (8). arXiv:hep-th/0507171. Bibcode:2005PhRvD..72h4013H. doi:10.1103/PhysRevD.72.084013.
- Hořava, Petr; Witten, Edward (1996). "Heterotic and Type I string dynamics from eleven dimensions". Nuclear Physics B. 460 (3): 506–524. arXiv:hep-th/9510209. Bibcode:1996NuPhB.460..506H. doi:10.1016/0550-3213(95)00621-4.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000037-QINU`"'</ref>" does not exist.
- Hull, Chris; Townsend, Paul (1995). "Unity of superstring dualities". Nuclear Physics B. 4381 (1): 109–137. arXiv:hep-th/9410167. Bibcode:1995NuPhB.438..109H. doi:10.1016/0550-3213(94)00559-W.
- Kapustin, Anton; Witten, Edward (2007). "Electric-magnetic duality and the geometric Langlands program". Communications in Number Theory and Physics. 1 (1): 1–236. arXiv:hep-th/0604151. Bibcode:2007CNTP....1....1K. doi:10.4310/cntp.2007.v1.n1.a1.
- Klarreich, Erica. "Mathematicians chase moonshine's shadow". Quanta Magazine. Retrieved March 2015.
{{cite web}}: Check date values in:|accessdate=(help) - Klebanov, Igor; Maldacena, Juan (2009). "Solving Quantum Field Theories via Curved Spacetimes" (PDF). Physics Today. 62: 28–33. Bibcode:2009PhT....62a..28K. doi:10.1063/1.3074260. Archived from the original (PDF) on 2013-07-02. Retrieved May 2013.
{{cite journal}}: Check date values in:|accessdate=(help); Unknown parameter|dead-url=ignored (|url-status=suggested) (help) - Kontsevich, Maxim (1995). "Homological algebra of mirror symmetry". Proceedings of the International Congress of Mathematicians: 120–139. arXiv:alg-geom/9411018. Bibcode:1994alg.geom.11018K.
- Kovtun, P. K.; Son, Dam T.; Starinets, A. O. (2001). "Viscosity in strongly interacting quantum field theories from black hole physics". Physical Review Letters. 94 (11): 111601. arXiv:hep-th/0405231. Bibcode:2005PhRvL..94k1601K. doi:10.1103/PhysRevLett.94.111601. PMID 15903845.
- Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (1997). "Mirror principle, I". Asian Journal of Math. 1: 729–763. arXiv:alg-geom/9712011. Bibcode:1997alg.geom.12011L.
- Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (1999a). "Mirror principle, II". Asian Journal of Math. 3: 109–146. arXiv:math/9905006. Bibcode:1999math......5006L.
- Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (1999b). "Mirror principle, III". Asian Journal of Math. 3: 771–800. arXiv:math/9912038. Bibcode:1999math.....12038L.
- Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (2000). "Mirror principle, IV". Surveys in Differential Geometry. 7: 475–496. arXiv:math/0007104. Bibcode:2000math......7104L. doi:10.4310/sdg.2002.v7.n1.a15.
- Luzum, Matthew; Romatschke, Paul (2008). "Conformal relativistic viscous hydrodynamics: Applications to RHIC results at √sNN=200 GeV". Physical Review C. 78 (3). arXiv:0804.4015. doi:10.1103/PhysRevC.78.034915.
- Maldacena, Juan (1998). "The Large N limit of superconformal field theories and supergravity". Advances in Theoretical and Mathematical Physics. 2: 231–252. arXiv:hep-th/9711200. Bibcode:1998AdTMP...2..231M. doi:10.1063/1.59653.
- Maldacena, Juan (2005). "The Illusion of Gravity" (PDF). Scientific American. 293 (5): 56–63. Bibcode:2005SciAm.293e..56M. doi:10.1038/scientificamerican1105-56. PMID 16318027. Archived from the original (PDF) on 2013-11-10. Retrieved July 2013.
{{cite journal}}: Check date values in:|accessdate=(help); Unknown parameter|dead-url=ignored (|url-status=suggested) (help) - Maldacena, Juan; Strominger, Andrew; Witten, Edward (1997). "Black hole entropy in M-theory". Journal of High Energy Physics. 1997 (12). doi:10.1088/1126-6708/1997/12/002.
- Merali, Zeeya (2011). "Collaborative physics: string theory finds a bench mate". Nature. 478 (7369): 302–304. Bibcode:2011Natur.478..302M. doi:10.1038/478302a. PMID 22012369.
- Moore, Gregory (2005). "What is ... a Brane?" (PDF). Notices of the AMS. 52: 214. Retrieved June 2013.
{{cite journal}}: Check date values in:|accessdate=(help) - Nahm, Walter (1978). "Supersymmetries and their representations". Nuclear Physics B. 135 (1): 149–166. Bibcode:1978NuPhB.135..149N. doi:10.1016/0550-3213(78)90218-3.
- Nekrasov, Nikita; Schwarz, Albert (1998). "Instantons on noncommutative R4 and (2,0) superconformal six dimensional theory". Communications in Mathematical Physics. 198 (3): 689–703. arXiv:hep-th/9802068. Bibcode:1998CMaPh.198..689N. doi:10.1007/s002200050490.
- Ooguri, Hirosi; Strominger, Andrew; Vafa, Cumrun (2004). "Black hole attractors and the topological string". Physical Review D. 70 (10). doi:10.1103/physrevd.70.106007.
- Polchinski, Joseph (2007). "All Strung Out?". American Scientist. Archived from the original on 2017-04-07. Retrieved April 2015.
{{cite journal}}: Check date values in:|accessdate=(help) - Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000052-QINU`"'</ref>" does not exist.
- Randall, Lisa; Sundrum, Raman (1999). "An alternative to compactification". Physical Review Letters. 83 (23): 4690–4693. arXiv:hep-th/9906064. Bibcode:1999PhRvL..83.4690R. doi:10.1103/PhysRevLett.83.4690.
- Sachdev, Subir (2013). "Strange and stringy". Scientific American. 308 (44): 44–51. Bibcode:2012SciAm.308a..44S. doi:10.1038/scientificamerican0113-44.
- Seiberg, Nathan; Witten, Edward (1999). "String Theory and Noncommutative Geometry". Journal of High Energy Physics. 1999 (9): 032. arXiv:hep-th/9908142. Bibcode:1999JHEP...09..032S. doi:10.1088/1126-6708/1999/09/032.
- Sen, Ashoke (1994a). "Strong-weak coupling duality in four-dimensional string theory". International Journal of Modern Physics A. 9 (21): 3707–3750. arXiv:hep-th/9402002. Bibcode:1994IJMPA...9.3707S. doi:10.1142/S0217751X94001497.
- Sen, Ashoke (1994b). "Dyon-monopole bound states, self-dual harmonic forms on the multi-monopole moduli space, and SL(2,Z) invariance in string theory". Physics Letters B. 329 (2): 217–221. arXiv:hep-th/9402032. Bibcode:1994PhLB..329..217S. doi:10.1016/0370-2693(94)90763-3.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000005A-QINU`"'</ref>" does not exist.
- Strominger, Andrew (1998). "Black hole entropy from near-horizon microstates". Journal of High Energy Physics. 1998 (2): 009. arXiv:hep-th/9712251. Bibcode:1998JHEP...02..009S. doi:10.1088/1126-6708/1998/02/009.
- Strominger, Andrew; Vafa, Cumrun (1996). "Microscopic origin of the Bekenstein–Hawking entropy". Physics Letters B. 379 (1): 99–104. arXiv:hep-th/9601029. Bibcode:1996PhLB..379...99S. doi:10.1016/0370-2693(96)00345-0.
- Strominger, Andrew; Yau, Shing-Tung; Zaslow, Eric (1996). "Mirror symmetry is T-duality". Nuclear Physics B. 479 (1): 243–259. arXiv:hep-th/9606040. Bibcode:1996NuPhB.479..243S. doi:10.1016/0550-3213(96)00434-8.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000005E-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000005F-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000060-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000061-QINU`"'</ref>" does not exist.
- Witten, Edward (1995). "String theory dynamics in various dimensions". Nuclear Physics B. 443 (1): 85–126. arXiv:hep-th/9503124. Bibcode:1995NuPhB.443...85W. doi:10.1016/0550-3213(95)00158-O.
- Witten, Edward (1998). "Anti-de Sitter space and holography". Advances in Theoretical and Mathematical Physics. 2: 253–291. arXiv:hep-th/9802150. Bibcode:1998AdTMP...2..253W.
- Witten, Edward (2007). "Three-dimensional gravity revisited". arXiv:0706.3359 [hep-th].
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000065-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000066-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000067-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000068-QINU`"'</ref>" does not exist.
ਹੋਰ ਅੱਗੇ ਪੜਾਈ
[ਸੋਧੋ]ਲੋਕ ਪ੍ਰਚਾਰ
[ਸੋਧੋ]ਸਰਵ ਸਧਾਰਨ
[ਸੋਧੋ]- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000069-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000006A-QINU`"'</ref>" does not exist.
ਅਲੋਚਨਾਤਮਿਕ
[ਸੋਧੋ]- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000006B-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000006C-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000006D-QINU`"'</ref>" does not exist.
ਪੁਸਤਕਾਂ
[ਸੋਧੋ]ਭੌਤਿਕ ਵਿਗਿਆਨੀਆਂ ਵਾਸਤੇ
[ਸੋਧੋ]- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000006E-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000006F-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000070-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000071-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000072-QINU`"'</ref>" does not exist.
- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000073-QINU`"'</ref>" does not exist.
ਗਣਿਤ ਸ਼ਾਸਤਰੀਆਂ ਵਾਸਤੇ
[ਸੋਧੋ]- Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000074-QINU`"'</ref>" does not exist.
