ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ
| ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ |
|---|
 |
| ਇਤਿਹਾਸ |
ਕਣ ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ, ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ (QED) ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਦੀ ਸਾਪੇਖਿਕ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਹੈ। ਸਾਰਾਂਸ਼ ਵਿੱਚ, ਇਹ ਦਰਸਾਉਂਦੀ ਹੈ ਕਿ ਕਿਵੇਂ ਪ੍ਰਕਾਸ਼ ਅਤੇ ਪਦਾਰਥ ਪਰਸਪਰ ਕ੍ਰਿਆ ਕਰਦੇ ਹਨ ਅਤੇ ਪਹਿਲੀ ਥਿਊਰੀ ਹੈ ਜਿਸਤੇ ਕੁਆਂਟਮ ਮਕੈਨਿਕਸ ਅਤੇ ਸਪੈਸ਼ਲ ਰਿਲੇਟੀਵਿਟੀ ਦਰਮਿਆਨ ਸੰਪੂਰਣ ਸਹਮਿਤੀ ਪ੍ਰਾਪਤ ਕੀਤੀ ਗਈ ਹੈ। QED ਗਣਿਤਿਕ ਤੌਰ ਤੇ ਉਹਨਾਂ ਸਾਰੇ ਘਟਨਾਕ੍ਰਮਾਂ ਨੂੰ ਸ਼ਾਮਲ ਕਰਦੀ ਹੈ ਜਿਹਨਾਂ ਵਿੱਚ ਇਲੈਕਟ੍ਰੀਕਲ ਤੌਰ ਤੇ ਚਾਰਜ ਹੋਏ ਕਣ ਫੋਟੌਨਾਂ ਦੇ ਵਟਾਂਦਰੇ ਦੇ ਅਰਥਾਂ ਰਾਹੀਂ ਪਰਸਪਰ ਕ੍ਰਿਆ ਕਰਦੇ ਹਨ ਅਤੇ ਪਦਾਰਥ ਅਰੇ ਪ੍ਰਕਾਸ਼ ਪਰਸਪਰ ਕ੍ਰਿਆ ਨੂੰ ਪੂਰੇ ਤੌਰ ਤੇ ਧਿਆਨ ਵਿੱਚ ਰੱਖਦੇ ਹੋਏ ਕਲਾਸੀਕਲ ਇਲੈਕਟ੍ਰੋਮੈਗਨਟਿਜ਼ਮ ਦੇ ਕੁਆਂਟਮ ਵਿਰੋਧੀਸਾਥੀ ਨੂੰ ਪੇਸ਼ ਕਰਦੇ ਹਨ।
ਤਕਨੀਕੀ ਭਾਸ਼ਾ ਵਿੱਚ, ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਨੂੰ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਕੁਆਂਟਮ ਵੈਕੱਮ ਦੀ ਪਰਚਰਬੇਸ਼ਨ ਥਿਊਰੀ ਦੇ ਤੌਰ ਤੇ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਰਿਚਰਡ ਫੇਨਮੈਨ ਨੇ ਇਸਨੂੰ ਇਸਦੇ, ਹਾਈਡ੍ਰੋਜਨ ਦੇ ਊਰਜਾ ਲੈਵਲਾਂ ਦੀ ਲੈਂਬ ਸ਼ਿਫਟ ਅਤੇ ਇਲੈਕਟ੍ਰੌਨ ਦੀ ਨਿਯਮਵਿਰੁੱਧ ਮੈਗਨੈਟਿਕ ਮੋਮੈਂਟ ਵਰਗੀਆਂ ਮਾਤਰਾਵਾਂ ਦੇ ਅਤਿ ਸ਼ੁੱਧ ਅਨੁਮਾਨਾਂ ਲਈ “ਭੌਤਿਕ ਵਿਗਿਆਨ ਦਾ ਗਹਿਣਾ” ਕਿਹਾ। [1]
ਇਤਿਹਾਸ
[ਸੋਧੋ]
ਰੇਡੀਏਸ਼ਨ ਅਤੇ ਪਦਾਰਥਕ ਪਰਸਪਰ ਕ੍ਰਿਆ ਦਰਸਾਉਂਦੀ ਕੁਆਂਟਮ ਥਿਊਰੀ ਦੀ ਪਹਿਲੀ ਫਾਰਮੂਲਾ ਬਣਤਰ ਸੂਤਰੀਕਰਨ ਦਾ ਸੇਹਰਾ ਬ੍ਰਿਟਿਸ਼ ਵਿਗਿਆਨਿਕ ਪੌਲ ਡੀਰਾਕ ਨੂੰ ਜਾਂਦਾ ਹੈ, ਜੋ (1920ਵੇਂ ਦਹਾਕੇ ਦੌਰਾਨ) ਕਿਸੇ ਐਟਮ ਦੇ ਤੁਰੰਤ ਨਿਕਾਸ ਦੇ ਗੁਣਾਂਕ ਦਾ ਪਤਾ ਲਗਾਉਣ ਵਿੱਚ ਸਫਲ ਨਹੀਂ ਹੋਇਆ ਸੀ। [2]
|bibcode = 1932RvMP....4...87F }}</ref>ਡੀਰਾਕ ਨੇ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਫੀਲਡ ਦੀ ਕੁਆਂਟਾਇਜ਼ੇਸ਼ਨ ਨੂੰ ਕਣਾਂ ਦੇ ਰਚਨਾਤਮਿਕ ਅਤੇ ਵਿਨਾਸ਼ਤਮਿਕ ਓਪਰੇਟਰਾਂ ਦੇ ਸੰਕਲਪ ਬਾਰੇ ਜਾਣ ਪਛਾਣ ਕਰਵਾ ਕੇ ਹਾਰਮੋਨਿਕ ਔਸੀਲੇਟਰਾਂ ਦੇ ਤੌਰ ਤੇ ਦਰਸਾਇਆ।
ਅਗਲੇ ਸਾਲਾਂ ਵਿੱਚ, ਵੁਲਫਗਾਂਗ ਪੌਲੀ, ਇਉਜੀਨ ਵਿਗਨਰ, ਪਾਸਕਲ ਜੌਰਡਨ, ਵਰਨਰ ਹੇਜ਼ਨਬਰਗ ਅਤੇ ਇੱਕ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਦੇ ਸ਼ਾਨਦਾਰ ਫਾਰਮੂਲਾ ਸੂਤਰੀਕਰਨ ਜੋ ਐਨ੍ਰੀਕੋ ਫਰਮੀ[3] ਕਾਰਨ ਸੀ, ਦੇ ਯੋਗਦਾਨ ਸਦਕਾ, ਭੌਤਿਕ ਵਿਗਿਆਨੀ ਇਹ ਯਕੀਨ ਕਰਨ ਲੱਗੇ ਕਿ, ਸਿਧਾਂਤ ਵਿੱਚ, ਫੋਟੌਨਾਂ ਅਤੇ ਚਾਰਜ ਕੀਤੇ ਕਣਾਂ ਵਾਲੀ ਕਿਸੇ ਭੌਤਿਕੀ ਪ੍ਰਕ੍ਰਿਆ ਲਈ ਕੋਈ ਵੀ ਹਿਸਾਬ ਕਿਤਾਬ ਲਗਾਉਣਾ ਸੰਭਵ ਹੋ ਸਕਦਾ ਹੈ। ਫੇਰ ਵੀ, ਫਲੈਕਸ ਬਲੋਚ ਦੇ ਅਰਨਾਲਡ ਨੌਰਡਸਿਕ</ref> and Victor Weisskopf,[4] ਅਤੇ ਵਿਕਟਰ ਵੇਸਕੌਫ[4] ਨਾਲ ਮਿਲ ਕੇ ਕੀਤੇ 1937 ਅਤੇ 1939 ਵਿੱਚ ਹੋਰ ਅੱਗੇ ਦੇ ਅਧਿਐਨਾਂ ਨੇ ਭੇਤ ਖੋਲਿਆ ਕਿ ਅਜਿਹੇ ਹਿਸਾਬ ਕਿਤਾਬ ਸਿਰਫ ਪਰਚਰਬੇਸ਼ਨ ਥਿਊਰੀ ਦੇ ਪਹਿਲੇ ਦਰਜੇ ਉੱਤੇ ਹੀ ਭਰੋਸੇਯੋਗ ਹੋ ਸਕਦੇ ਸਨ, ਜੋ ਅਜਿਹੀ ਸਮੱਸਿਆ ਸੀ। ਜਿਸ ਬਾਰੇ ਪਹਿਲਾਂ ਹੀ ਰੌਬਰਟ ਅੱਪਨਹੀਮਰ[5] ਨੇ ਇਸ਼ਾਰਾ ਕੀਤਾ ਸੀ। ਲੜੀਆਂ ਵਿੱਚ ਉੱਚ ਦਰਜਿਆਂ ਉੱਤੇ ਅਨੰਤ ਪੈਦਾ ਹੋ ਜਾਂਦੇ ਹਨ, ਜੋ ਅਜਿਹੇ ਹਿਸਾਬ ਕਿਤਾਬਾਂ ਨੂੰ ਅਰਥਹੀਣ ਬਣਾਉਂਦੇ ਹੋਏ ਥਿਊਰੀ ਦੀ ਅਪਣੀ ਅੰਦਰੂਨੀ ਸਥਿਰਤਾ ਉੱਤੇ ਗੰਭੀਰ ਸ਼ੱਕ ਪੈਦਾ ਕਰਦੇ ਹਨ। ਵਕਤ ਉੱਤੇ ਇਸ ਸਮੱਸਿਆ ਦੇ ਅਣਸੁਲ਼ਝੇ ਹੱਲ ਨਾਲ, ਇਹ ਨਜ਼ਰ ਆਇਆ ਹੈ ਕਿ ਸਪੈਸ਼ਲ ਰਿਲੇਟੀਵਿਟੀ ਅਤੇ ਕੁਆਂਟਮ ਮਕੈਨਿਕਸ ਦਰਮਿਆਨ ਇੱਕ ਮੁਢਲੀ ਬੇਮੇਲਤਾ ਮੌਜੂਦ ਰਹਿੰਦੀ ਹੈ।

1940 ਦੇ ਅੰਤ ਵਿੱਚ ਥਿਊਰੀ ਨਾਲ ਸਮੱਸਿਆਵਾਂ ਵਧ ਗਈਆਂ। ਮਾਈਕ੍ਰੋਵੇਵ ਤਕਨੀਕ ਵਿੱਚ ਸੁਧਾਰਾਂ ਨੇ ਹਾਈਡ੍ਰੋਜਨ ਐਟਮ[6] ਦੇ ਲੈਵਲਾਂ ਦੇ ਖਿਸਕਾਓ ਦੇ ਹੋਰ ਸ਼ੁੱਧ ਨਾਪਾਂ ਨੂੰ ਲੈਣਾ ਸੰਭਵ ਕੀਤਾ, ਜਿਸਨੂੰ ਲੈਂਬ ਸ਼ਿਫਟ ਅਤੇ ਇਲੈਕਟ੍ਰੌਨ ਦੀ ਚੁੰਬਕੀ ਮੋਮੈਂਟ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।[7] ਇਹਨਾਂ ਪ੍ਰਯੋਗਾਂ ਨੇ ਸਪੱਸ਼ਟ ਰੂਪ ਵਿੱਚ ਉਹਨਾਂ ਵਿਸੰਗਤੀਆਂ ਨੂੰ ਸਾਹਮਣੇ ਲਿਆਂਦਾ ਜਿਹਨਾਂ ਬਾਰੇ ਥਿਊਰੀ ਸਮਝਾਉਣ ਤੋਂ ਅਸਮਰਥ ਰਹੀ ਸੀ।
ਇੱਕ ਸੰਭਵ ਤਰੀਕੇ ਦਾ ਪਹਿਲਾ ਸੰਕੇਤ ਹੰਸ ਬੈਥੇ ਦੁਆਰਾ ਦਿੱਤਾ ਗਿਆ ਸੀ। 1947 ਵਿੱਚ, ਜਦੋਂ ਉਹ ਨਿਊਯੌਰਕ ਤੋਂ ਸ਼ੈਨੇਕਟਡੀ ਪਹੁੰਚਣ ਲਈ ਰੇਲਗੱਡੀ ਵਿੱਚ ਯਾਤਰਾ ਕਰ ਰਿਹਾ ਸੀ[8], ਤਾਂ ਸ਼ੈਲਟਰ ਆਈਸਲੈਂਡ ਵਿਖੇ ਵਿਸ਼ੇ ਉੱਤੇ ਭਾਸ਼ਣ ਦੇਣ ਤੋਂ ਬਾਦ, ਬੈਥੇ ਨੇ ਲੈਂਬ ਅਤੇ ਰੇਥਰਫੋਰਡ[9] ਦੁਆਰਾ ਨਾਪੀਆਂ ਹਾਈਡ੍ਰੋਜਨ ਐਟਮ ਦੀਆਂ ਰੇਖਾਵਾਂ ਦੇ ਖਿਸਕਾਓ ਦੇ ਪਹਿਲੇ ਗੈਰ-ਸਾਪੇਖਿਕ ਹਿਸਾਬ ਕਿਤਾਬ ਨੂੰ ਪੂਰਾ ਕੀਤਾ। ਹਿਸਾਬ ਕਿਤਾਬ ਦੀਆਂ ਕਮੀਆਂ ਦੇ ਬਾਵਜੂਦ, ਸਹਿਮਤੀ ਸ਼ਾਨਦਾਰ ਸੀ। ਵਿਚਾਰ ਸਰਲਤਾ ਨਾਲ ਇਹ ਸੀ ਕਿ ਪ੍ਰਯੋਗਾਂ ਰਾਹੀਂ ਇੱਕ ਸੀਮਤ ਮੁੱਲ ਨਿਰਧਾਰਿਤ ਕੀਤੇ ਹੋਏ ਪੁੰਜ ਅਤੇ ਚਾਰਜ ਦੇ ਸੁਧਾਰਾਂ ਪ੍ਰਤਿ ਅਨੰਤਾਂ ਨੂੰ ਜੋੜਨਾ ਹੈ। ਇਸ ਤਰੀਕੇ ਨਾਲ, ਅਨੰਤ ਉਹਨਾਂ ਸਥਿਰਾਂਕਾਂ ਵਿੱਚ ਸੋਖ ਲਏ ਜਾਂਦੇ ਹਨ ਅਤੇ ਪ੍ਰਯੋਗਾਂ ਨਾਲ ਚੰਗੀ ਸਹਿਮਤੀ ਵਿੱਚ ਇੱਕ ਸੀਮਤ ਨਤੀਜਾ ਪੈਦਾ ਕਰਦੇ ਹਨ। ਇਸ ਵਿਧੀ ਨੂੰ ਪੁਨਰਮਾਨਕੀਕਰਨ (ਰੀਨੌਰਮਲਾਈਜ਼ੇਸ਼ਨ) ਦਾ ਨਾਮ ਦਿੱਤਾ ਗਿਆ।

ਬੈਥੇ ਦੇ ਸਹਿਜ ਗਿਆਨ ਅਤੇ ਸਿਨ-ਲਤੀਰੋ ਟੋਮੋਨਾਗਾ[10], ਜੂਲੀਅਨ ਸ਼ਵਿੰਗਰ,[11][12] ਰਿਚਰਡ ਫੇਨਮੈਨ[13][14][15] ਅਤੇ ਫਰੀਮੈਨ ਡੇਅਸਨ[16][17] ਦੁਆਰਾ ਵਿਸ਼ੇ ਉੱਤੇ ਬੁਨਿਆਦੀ ਪੇਪਰਾਂ ਉੱਤੇ ਅਧਾਰਿਤ, ਅੰਤ ਵਿੱਚ ਪੂਰੀ ਤਰਾਂ ਕੋਵੇਰੀਅੰਟ ਫਾਰਮੂਲਾ ਵਿਊਂਤਬੰਦੀਆਂ ਪ੍ਰਾਪਤ ਕਰਨੀਆਂ ਸੰਭਵ ਹੋ ਗਈਆਂ ਜੋ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਦੀਆਂ ਪਰਚਰਬੇਸ਼ਨ ਲੜੀਆਂ ਵਿੱਚ ਕਿਸੇ ਵੀ ਦਰਜੇ ਉੱਤੇ ਸੀਮਤ ਸਨ। ਸਿਨ-ਲਤੀਰੋ ਟੋਮੋਨਾਗਾ, ਜੂਲੀਅਨ ਸ਼ਵਿੰਗਰ ਅਤੇ ਰਿਚਰਡ ਫੇਨਮੈਨ ਨੇ ਇਕੱਠੇ ਹੋ ਕੇ ਇਸ ਖੇਤਰ ਵਿੱਚ ਅਪਣੇ ਕੰਮ ਲਈ 1965 ਵਿੱਚ ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ ਨੋਬਲ ਪੁਰਸਕਾਰ ਪ੍ਰਾਪਤ ਕੀਤਾ। ਉਹਨਾਂ ਦੇ ਯੋਗਦਾਨ, ਅਤੇ ਫਰੀਮੈਨ ਡੇਅਸਨ ਦਾ ਯੋਗਦਾਨ, ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਦੇ ਕੋਵੇਰੀਅੰਟ ਅਤੇ ਗੇਜ ਇਨਵੇਰੀਅੰਟ ਫਾਰਮੂਲਿਆਂ ਬਾਰੇ ਸੀ, ਜੋ ਪਰਚਰਬੇਸ਼ਨ ਥਿਊਰੀ ਦੇ ਕਿਸੇ ਦਰਜੇ ਉੱਤੇ ਨਿਰੀਖਣਾਂ ਦੇ ਹਿਸਾਬ ਕਿਤਾਬ ਪਤਾ ਕਰਨ ਦੀ ਆਗਿਆ ਦਿੰਦੇ ਹਨ। ਫੇਨਮੈਨ ਦੀ ਗਣਿਤਿਕ ਤਕਨੀਕ, ਜੋ ਉਸਦੇ ਚਿੱਤਰਾਂ ਉੱਤੇ ਅਧਾਰਿਤ ਹੈ, ਸ਼ੁਰੂ ਸ਼ੁਰੂ ਵਿੱਚ ਫੀਲਡ-ਥਿਊਰੈਟਿਕ ਤੋਂ ਬਹੁਤ ਵੱਖਰੀ ਲਗਦੀ ਸੀ ਜੋ ਸ਼ਵਿੰਗਰ ਅਤੇ ਟੋਮੋਨਾਗਾ ਦੀ ਓਪਰੇਟਰ-ਅਧਾਰਿਤ ਪਹੁੰਚ ਸੀ, ਪਰ ਫਰੀਮੈਨ ਡੇਅਸਨ ਨੇ ਬਾਦ ਵਿੱਚ ਸਾਬਤ ਕੀਤਾ ਕਿ ਦੋਵੇਂ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਸਮਾਨ ਹੀ ਸਨ। ਪੁਨਰਮਾਨਕੀਕਰਨ, ਜੋ ਇੰਟਗ੍ਰਲਾਂ ਰਾਹੀਂ ਥਿਊਰੀ ਵਿੱਚ ਦਿਸਦੇ ਨਿਸ਼ਚਿਤ ਡਾਇਵਰਜੰਸਾਂ ਉੱਤੇ ਇੱਕ ਭੌਤਿਕੀ ਅਰਥ ਜੋੜਨ ਦੀ ਜਰੂਰਤ ਹੈ, ਬਾਦ ਵਿੱਚ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਦੇ ਬੁਨਿਆਦੀ ਪਹਿਲੂਆਂ ਵਿੱਚੋਂ ਇੱਕ ਬਣ ਗਈ ਅਤੇ ਕਿਸੇ ਥਿਊਰੀ ਦੀ ਸਰਵ ਸਧਾਰਨ ਸਵੀਕ੍ਰਿਤੀ ਲਈ ਇੱਕ ਸਾਧਨ ਦੇ ਤੌਰ ਤੇ ਦੇਖੀ ਜਾਣ ਲੱਗੀ ਹੈ। ਭਾਵੇਂ ਰੀਨੌਰਮਲਾਇਜ਼ੇਸ਼ਨ (ਪੁਨਰਮਾਨਕੀਕਰਨ) ਅਭਿਆਸ ਵਿੱਚ ਬਹੁਤ ਚੰਗੀ ਤਰਾਂ ਕੰਮ ਕਰਦੀ ਹੈ, ਫੇਰ ਵੀ ਫੇਨਮੈਨ ਇਸਦੀ ਗਣਿਤਿਕ ਪ੍ਰਮਾਣਿਕਤਾ ਨਾਲ ਕਦੇ ਵੀ ਪੂਰੀ ਤਰਾਂ ਸਹਿਮਤ ਨਹੀਂ ਹੋਇਆ ਸੀ, ਇੱਥੋਂ ਤੱਕ ਕਿ ਪੁਨਰਮਾਨਕੀਕਰਨ ਨੂੰ ਇੱਕ “ਸ਼ੈੱਲ ਗੇਮ” ਅਤੇ “ਹੋਕੁਸ ਪੋਕੁਸ” (ਧੋਖਾ ਦੇਣਾ) ਦੇ ਤੌਰ ਤੇ ਇਸ਼ਾਰਾ ਕਰਦਾ ਸੀ।
ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਨੇ ਸਾਰੀਆਂ ਬਾਦ ਵਾਲੀਆਂ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀਆਂ ਲਈ ਮਾਡਲ ਅਤੇ ਨਮੂਨੇ ਦੇ ਤੌਰ ਤੇ ਭੂਮਿਕਾ ਨਿਭਾਈ ਹੈ। ਇੱਕ ਹੋਰ ਅਜਿਹੀ ਬਾਦ ਵਾਲੀ ਥਿਊਰੀ ਕੁਆਂਟਮ ਕ੍ਰੋਮੋਡਾਇਨਾਮਿਕਸ ਹੈ, ਜੋ 1960ਵੇਂ ਦਹਾਕੇ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਸ਼ੁਰੂ ਹੋਈ ਸੀ। ਅਤੇ ਅਪਣੀ ਮੌਜੂਦਾ ਕਿਸਮ ਐੱਚ. ਡੇਵਿਡ ਪੋਲੀਟਜ਼ਰ, ਸਿਡਨੇ ਕੋਲੇਮਨ, ਡੇਵਿਡ ਗ੍ਰੌਸ, ਅਤੇ ਫ੍ਰੈਂਕ ਵਿਲਜ਼ੱਕ ਦੁਆਰਾ 1975 ਵਿੱਚ ਆਈ। ਸ਼ਵਿੰਗਰ, ਗੇਰਾਲਡ ਗੁਰਾਲਨਿਕ, ਡਿਕ ਹਾਗਨ, ਅਤੇ ਟੌਮ ਕਿੱਬਲ, ਪੀਟਰ ਹਿੱਗਜ਼, ਜੈੱਫ੍ਰੀ ਗੋਲਡਸਟੋਨ ਅਤੇ ਹੋਰਾਂ ਦੀਆਂ ਖੋਜਾਂ ਉੱਤੇ ਬਣਾਉਂਦੇ ਹੋਏ, ਸ਼ੈਲਡਨ ਗਲਾਸ਼ੋਅ, ਸਟੀਵਨ ਵੇਨਬਰਗ ਅਤੇ ਅਬਡਸ ਸਾਲਮ ਨੇ ਸੁਤੰਤਰ ਤੌਰ ਤੇ ਦਿਖਾਇਆ ਕਿ ਕਿਵੇਂ ਕਮਜੋਰ ਨਿਊਕਲੀਅਰ ਬਲ ਅਤੇ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਇੱਕੋ ਸਿੰਗਲ ਇਲੈਕਟ੍ਰੋਵੀਕ ਫੋਰਸ ਵਿੱਚ ਇੱਕਠੇ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ।
ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਪ੍ਰਤਿ ਫੇਨਮੈਨ ਦਾ ਨਜ਼ਰੀਆ
[ਸੋਧੋ]ਜਾਣ ਪਛਾਣ
[ਸੋਧੋ]ਅਪਣੀ ਜਿੰਦਗੀ ਦੇ ਅੰਤ ਦੇ ਨੇੜੇ, ਰਿਚਰਡ ਪੀ. ਫੇਨਮੈਨ ਨੇ ਆਮ ਜਨਤਾ ਨੂੰ ਧਿਆਨ ਵਿੱਚ ਰੱਖ ਕੇ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਉੱਤੇ ਲੈਕਚਰਾਂ ਦੀ ਇੱਕ ਸੀਰੀਜ਼ ਦਿੱਤੀ। ਇਹ ਲੈਕਚਰ ਫੇਨਮੈਨ ਦੀ ਲਿਖਤ ਸਨ ਜੋ ਫੇਨਮੈਨ (1985), ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ: ਦਿ ਸਟ੍ਰੇਂਜ ਥਿਊਰੀ ਆਫ ਲਾਈਟ ਐਂਡ ਮੈਟਰ, (ਪ੍ਰਕਾਸ਼ ਅਤੇ ਪਦਾਰਥ ਦੀ ਅਨੋਖੀ ਥਿਊਰੀ) ਦੇ ਨਾਮ ਛਾਪੇ ਗਏ, ਜੋ ਹੇਠਾਂ ਦਰਸਾਏ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਤੋਂ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਦੀ ਇੱਕ ਗੈਰ-ਗਣਿਤਿਕ ਕਲਾਸੀਕਲ ਪ੍ਰਦਰਸ਼ਨੀ ਹੈ।
ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਦੀ ਫੇਨਮੈਨ ਦੀ ਪੇਸ਼ਕਸ਼ ਦੇ ਪ੍ਰਮੁੱਖ ਹਿੱਸੇ ਤਿੰਨ ਬੁਨਿਆਦੀ ਕਾਰਜ ਹਨ।
- ਇੱਕ ਫੋਟੌਨ ਇੱਕ ਸਥਾਨ ਅਤੇ ਵਕਤ ਤੋਂ ਇੱਕ ਹੋਰ ਸਥਾਨ ਅਤੇ ਵਕਤ ਤੱਕ ਜਾਂਦਾ ਹੈ।
- ਇੱਕ ਇਲੈਕਟ੍ਰੌਨ ਇੱਕ ਸਥਾਨ ਅਤੇ ਵਕਤ ਤੋਂ ਇੱਕ ਹੋਰ ਸਥਾਨ ਅਤੇ ਵਕਤ ਤੱਕ ਜਾਂਦਾ ਹੈ।
- ਇੱਕ ਇਲੈਕਟ੍ਰੌਨ ਇੱਕ ਨਿਸ਼ਚਿਤ ਸਥਾਨ ਅਤੇ ਵਕਤ ਉੱਤੇ ਇੱਕ ਫੋਟੌਨ ਦਾ ਨਿਕਾਸ ਕਰਦਾ ਹੈ ਜਾਂ ਇੱਕ ਫੋਟੌਨ ਨੂੰ ਸੋਖ ਲੈਂਦਾ ਹੈ।

ਇਹ ਕਾਰਜ ਫੇਨਮੈਨ ਚਿੱਤਰਾਂ ਦੇ ਤਿੰਨ ਬੁਨਿਆਦੀ ਤੱਤਾਂ ਰਾਹੀਂ ਦ੍ਰਿਸ਼ ਸੰਖੇਪ ਸੰਕੇਤਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਪ੍ਰਸਤੁਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ: ਫੋਟੌਨ ਲਈ ਇੱਕ ਤਰੰਗੀ ਰੇਖਾ, ਇਲੈਕਟ੍ਰੌਨ ਲਈ ਇੱਕ ਸਿੱਧੀ ਰੇਖਾ ਅਤੇ ਦੋ ਸਿੱਧੀਆਂ ਰੇਖਾਵਾਂ ਅਤੇ ਇੱਕ ਤਰੰਗੀ ਰੇਖਾ ਦਾ ਜੰਕਸ਼ਨ ਕਿਸੇ ਇਲੈਕਟ੍ਰੌਨ ਦੁਆਰਾ ਇੱਕ ਫੋਟੌਨ ਦੇ ਸੋਖੇ ਜਾਣ ਜਾਂ ਨਿਕਾਸ ਨੂੰ ਪ੍ਰਸਤੁਤ ਕਰਦੇ ਹੋਇਆ ਇੱਕ ਸ਼ਿਖਰ ਲਈ। ਇਹਨਾਂ ਸਭ ਨੂੰ ਨਾਲ ਦਿਖਾਏ ਚਿੱਤਰ ਵਿੱਚ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ।
ਇਹਨਾਂ ਚਿੱਤਰਾਂ ਦੀ ਅਤਿਕਥਨੀ ਨਾ ਕਰਨੀ ਮਹੱਤਵਪੂਰਨ ਹੈ। ਕੁੱਝ ਵੀ ਅਜਿਹਾ ਭਾਵ ਨਹੀਂ ਦਿੱਤਾ ਗਿਆ ਕਿ ਕਿਵੇਂ ਇੱਕ ਕਣ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਦੂਜੇ ਬਿੰਦੂ ਤੱਕ ਜਾਂਦਾ ਹੈ। ਚਿੱਤਰ ਇਹ ਅਰਥ ਨਹੀਂ ਦਰਸਾਉਂਦੇ ਕਿ ਕਣ ਸਿੱਧੀਆਂ ਰੇਖਾ ਵਿੱਚ ਗਤੀਸ਼ੀਲ ਹਨ ਜਾਂ ਵਕਰਿਤ ਰੇਖਾਵਾਂ ਵਿੱਚ ਗਤੀ ਕਰਦੇ ਹਨ। ਇਹਨਾਂ ਤੋਂ ਇਹ ਭਾਵ ਵੀ ਨਹੀਂ ਹੈ ਕਿ ਕਣ ਸਥਿਰ ਸਪੀਡਾਂ ਨਾਲ ਗਤੀ ਕਰਦੇ ਹਨ। ਫੋਟੌਨਾਂ ਦਾ ਇੱਕ ਸਿੱਧੀ ਰੇਖਾ ਦੀ ਵਜਾਏ ਤਰੰਗੀ ਰੇਖਾ ਵਿੱਚ ਗਤੀਸ਼ੀਲ ਹੋਣਾ ਪ੍ਰਸਤੁਤ ਕੀਤੇ ਜਾਣ ਦੀ ਪ੍ਰੰਪਰਾ ਦਾ ਤੱਥ ਇਹ ਭਾਵ ਨਹੀਂ ਰੱਖਦਾ ਕਿ ਇਹ ਸੋਚਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਇਹ ਇਲੈਕਟ੍ਰੌਨ ਤੋਂ ਜਿਆਦਾ ਤਰੰਗ ਵਰਗਾ ਵਰਤਾਓ ਕਰਦਾ ਹੈ। ਉੱਪਰ ਲਿਖੇ ਕਾਰਜਾਂ ਨੂੰ ਪ੍ਰਸਤੁਤ ਕਰਨ ਲਈ ਤਸਵੀਰਾਂ ਸਿਰਫ ਚਿੰਨ ਹਨ: ਫੋਟੌਨ ਅਤੇ ਇਲੈਕਟ੍ਰੌਨ, ਕਿਵੇਂ ਨਾ ਕਿਵੇਂ, ਬਿੰਦੂ ਤੋਂ ਬਿੰਦੂ ਤੱਕ ਗਤੀ ਕਰਦੇ ਹਨ, ਅਤੇ ਇਲੈਕਟ੍ਰੌਨ ਕਿਵੇਂ ਨਾ ਕਿਵੇਂ ਫੋਟੌਨਾਂ ਨੂੰ ਸੋਖਦੇ ਅਤੇ ਨਿਕਾਸਦੇ ਹਨ। ਅਸੀਂ ਨਹੀਂ ਜਾਣਦੇ ਕਿ ਕਿਵੇਂ ਇਹ ਕੁੱਝ ਵਾਪਰਦਾ ਹੈ, ਪਰ ਥਿਊਰੀ ਸਾਨੂੰ ਇਹਨਾਂ ਚੀਜ਼ਾਂ ਦੇ ਵਾਪਰਨ ਦੀਆਂ ਪ੍ਰੋਬੇਬਿਲਟੀਆਂ (ਸੰਭਾਵਨਾਵਾਂ) ਬਾਰੇ ਦੱਸਦੀ ਹੈ।
ਜਿਵੇਂ ਕਾਰਜਾਂ ਲਈ ਫੇਨਮੈਨ ਨੇ ਦ੍ਰਿਸ਼ ਸੰਖੇਪ ਸੰਕੇਤਾਂ ਨਾਲ ਜਾਣ ਪਛਾਣ ਕਰਵਾਈ ਇਸੇ ਤਰਾਂ ਫੇਨਮੈਨ ਨੇ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡਾਂ ਨਾਮਕ ਸੰਖਿਅਕ ਮਾਤਰਾਵਾਂ ਲਈ ਵੀ ਇੱਕ ਹੋਰ ਕਿਸਮ ਦੇ ਸੰਖੇਪ ਸੰਕੇਤ ਪੇਸ਼ ਕੀਤੇ। ਪ੍ਰੋਬੇਬਿਲਟੀ ਕੁੱਲ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡ ਦਾ ਵਰਗ ਹੁੰਦੀ ਹੈ। ਜੇਕਰ ਕੋਈ ਫੋਟੌਨ ਇੱਕ ਸਥਾਨ ਅਤੇ ਵਕਤ- ਸੰਖੇਪ ਸੰਕੇਤ A – ਤੋਂ- ਦੀਜੇ ਸਥਾਨ ਅਤੇ ਵਕਤ – B- ਤੱਕ ਗਤੀ ਕਰਦਾ ਹੈ, ਤਾਂ ਸਬੰਧਤ ਮਾਤਰਾ ਨੂੰ ਫੇਨਮੈਨ ਸੰਖੇਪ ਸੰਕੇਤ ਪ੍ਰਣਾਲੀ ਵਿੱਚ P(A ਤੋਂ B) ਲਿਖਿਆ ਜਾਂਦਾ ਹੈ। ਕਿਸੇ ਇਲੈਕਟ੍ਰੌਨ ਲਈ ਇਹੀ ਮਾਤਰਾ E(C ਤੋਂ D) ਲਿਖੀ ਜਾਂਦੀ ਹੈ ਜੋ C ਤੋਂ D ਤੱਕ ਗਤੀ ਕਰਦਾ ਹੈ। ਜੋ ਮਾਤਰਾ ਸਾਨੂੰ ਕਿਸੇ ਫੋਟੌਨ ਦੇ ਸੋਖੇ ਜਾਣ ਜਾਂ ਨਿਕਾਸ ਲਈ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਉਡ ਬਾਰੇ ਦੱਸਦੀ ਹੈ ਉਸਨੂੰ ਉਸਨੇ “j” ਕਿਹਾ। ਇਹ ਇਲੈਕਟ੍ਰੌਨ ਚਾਰਜ “e” ਨਾਪਣ ਵਾਂਗ ਨਹੀਂ ਹੈ, ਪਰ ਇਸ ਨਾਲ ਸਬੰਧਤ ਹੈ।
ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਇਸ ਮਾਨਤਾ ਉੱਤੇ ਅਧਾਰਿਤ ਹੈ ਕਿ ਬਹੁਤ ਸਾਰੇ ਇਲੈਕਟ੍ਰੌਨਾਂ ਅਤੇ ਫੋਟੌਨਾਂ ਦੀਆਂ ਗੁੰਝਲਦਾਰ ਪਰਸਪਰ ਕ੍ਰਿਆਵਾਂ ਨੂੰ ਉੱਪਰ ਦਰਸਾਏ ਤਿੰਨ ਬੁਨਿਆਦੀ ਕਾਰਜਾਂ ਦੇ ਢੁਕਵੇਂ ਸਮੂਹ ਨੂੰ ਇਕੱਠਾ ਫਿੱਟ ਕਰਕੇ ਪ੍ਰਸਤੁਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਇਹ ਨਤੀਜਾ ਨਿਕਲਦਾ ਹੈ ਕਿ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਦਾ ਮੁਢਲਾ ਵਿਚਾਰਇਹ ਧਾਰਨਾ ਬਣਾ ਕੇ ਪ੍ਰਸਾਰਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਉੱਪਰ ਦਰਸਾਏ (P(A ਤੋਂ B), E(A ਤੋਂ B) ਅਤੇ 'j') ਕੁੱਲ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡਾਂ ਦਾ ਵਰਗ ਸਿਰਫ ਇੱਕ ਰੋਜ਼ਾਨਾ “ਸ਼ਾਇਦ” (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਵਾਂਗ ਕ੍ਰਿਆ ਕਰਦਾ ਹੈ। ਬਾਦ ਵਿੱਚ, ਫੇਨਮੈਨ ਨੂੰ ਅਪਣਾਉਂਦੇ ਹੋਏ, ਇਸਨੂੰ ਸੁਧਾਰ ਕੇ ਇਸ ਵਿੱਚ ਵਿਸ਼ੇਸ਼ ਤੌਰ ਤੇ ਕੁਆਂਟਮ-ਅੰਦਾਜ਼ ਗਣਿਤ ਸ਼ਾਮਿਲ ਕੀਤਾ ਜਾਵੇਗਾ।
ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡਾਂ ਦੇ ਬੁਨਿਆਦੀ ਕਨੂੰਨ ਜੋ ਵਰਤੇ ਜਾਣਗੇ ਇਹ ਹਨ;
- ਜੇਕਰ ਕੋਈ ਘਟਨਾ ਵਿਭਿੰਨ ਵੱਖਰੇ ਤਰੀਕਿਆਂ ਨਾਲ ਵਾਪਰ ਸਕਦੀ ਹੋਵੇ, ਤਾਂ ਇਸਦਾ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡ ਸੰਭਵ ਤਰੀਕਿਆਂ ਦੇ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡਾਂ ਦਾ ਜੋੜ ਹੁੰਦਾ ਹੈ।
- ਜੇਕਰ ਕੋਈ ਪ੍ਰਕ੍ਰਿਆ ਬਹੁਤ ਸਾਰੀਆਂ ਸੁਤੰਤਰ ਉੱਪ-ਪ੍ਰਕ੍ਰਿਆਵਾਂ ਸਮੇਤ ਹੋਵੇ ਤਾਂ ਇਸਦਾ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡ ਹਿੱਸਿਆਂ ਦੇ ਪ੍ਰੋਬਿਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡਾਂ ਦੇ ਗੁਣਨਫਲ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।
ਬੁਨਿਆਦੀ ਬਣਤਰਾਂ
[ਸੋਧੋ]ਮੰਨ ਲਓ ਅਸੀਂ ਕਿਸੇ ਨਿਸ਼ਚਿਤ ਸਥਾਨ ਅਤੇ ਵਕਤ (ਇਸ ਸਥਾਨ ਅਤੇ ਵਕਤ ਨੂੰ ਮਨਚਾਹਿਆ ਨਾਮਕਰਨ A ਦਿੱਤਾ ਜਾ ਸਕਦਾ ਹੈ) ਉੱਤੇ ਇੱਕ ਇਲੈਕਟ੍ਰੌਨ ਅਤੇ ਕਿਸੇ ਹੋਰ ਸਥਾਨ ਅਤੇ ਵਕਤ (ਜਿਸਨੂੰ B ਨਾਮ ਦਿੱਤਾ ਗਿਆ ਹੋਵੇ) ਉੱਤੇ ਇੱਕ ਫੋਟੌਨ ਨਾਲ ਸ਼ੁਰੂ ਕਰਦੇ ਹਾਂ। ਕਿਸੇ ਭੌਤਿਕੀ ਨਜ਼ਰੀਏ ਤੋਂ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਸਵਾਲ ਇਹ ਹੈ: ਕਿਸੇ ਇਲੈਕਟ੍ਰੌਨ ਨੂੰ C (ਇੱਕ ਹੋਰ ਸਥਾਨ ਅਤੇ ਬਾਦ ਵਾਲੇ ਵਕਤ) ਅਤੇ ਇੱਕ ਫੋਟੌਨ ਨੂੰ D (ਇੱਕ ਹੋਰ ਸਥਾਨ ਅਤੇ ਵਕਤ) ਉੱਤੇ ਖੋਜਣ ਦੀ ਖੋਜਣਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਕੀ ਹੈ?। ਇਸ ਸਿਰੇ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸਰਲਤਮ ਕ੍ਰਿਆ, ਇਲੈਕਟ੍ਰੌਨ ਲਈ A ਤੋਂ C ਤੱਕ ਗਤੀ ਕਰਨ ਦੀ (ਇੱਕ ਮੁਢਲੇ ਕਾਰਜ) ਅਤੇ ਫੋਟੌਨ ਲਈ B ਤੋਂ D ਤੱਕ ਗਤੀ ਕਰਨ ਦੀ (ਇੱਕ ਹੋਰ ਮੁਢਲੇ ਕਾਰਜ) ਹੈ। ਇਹਨਾਂ ਉੱਪ-ਪ੍ਰਕ੍ਰਿਆਵਾਂ E(A ਤੋਂ C) ਅਤੇ P(B ਤੋਂ D) ਵਿੱਚੋਂ ਹਰੇਕ ਦੇ ਖੋਜਯੋਗਤਾ ਐਂਪਲੀਟਿਊਡਾਂ ਦੀ ਜਾਣਕਾਰੀ ਤੋਂ- ਫੇਰ ਅਸੀਂ ਉੱਪਰ ਦਰਸਾਏ ਦੂਜੇ ਕਨੂੰਨ ਦੀ ਵਰਤੋਂ ਨਾਲ ਇਹਨਾਂ ਨੂੰ ਗੁਣਾਂ ਕਰਕੇ ਦੋਵੇਂ ਇਕੱਠੀਆਂ ਘਟਨਾਵਾਂ ਦੇ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡਾਂ ਦਾ ਪਤਾ ਲਗਾਉਣ ਦੀ ਉਮੀਦ ਕਰ ਸਕਦੇ ਹਾਂ। ਇਹ ਇੱਕ ਸਰਲ ਅਨੁਮਾਨਿਤ ਕੀਤਾ ਹੋਇਆ ਸਾਰੇ ਦਾ ਸਾਰਾ ਖੋਜਯੋਗਤਾ ਐਂਪਲੀਟਿਊਡ ਦਿੰਦਾ ਹੈ, ਜਿਸਦਾ ਇੱਕ ਅਨੁਮਾਨਿਤ ਖੋਜਯੋਗਤਾ ਦੇਣ ਲਈ ਵਰਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ।

ਪਰ ਹੋਰ ਤਰੀਕੇ ਵੀ ਹੁੰਦੇ ਹਨ ਜਿਹਨਾਂ ਵਿੱਚ ਅੰਤਿਮ ਨਤੀਜਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਇਲੈਕਟ੍ਰੌਨ ਹੋ ਸਕਦਾ ਹੈ ਕਿ ਇੱਕ ਸਥਾਨ ਅਤੇ ਵਕਤ E ਤੱਕ ਗਤੀ ਕਰਦਾ ਗਿਆ ਹੋਵੇ ਜਿੱਥੇ ਇਹ ਫੋਟੌਨ ਨੂੰ ਸੋਖ ਗਿਆ ਹੋਵੇ; ਫੇਰ F ਉੱਤੇ ਇੱਕ ਹੋਰ ਫੋਟੌਨ ਦਾ ਨਿਕਾਸ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਅੱਗੇ ਵਧਿਆ ਹੋਵੇ; ਫੇਰ C ਤੱਕ ਗਤੀ ਕਰਦਾ ਹੋਵੇ ਜਿੱਥੇ ਇਹ ਡਿਕੈਕਟ ਕਰ ਲਿਆ ਜਾਂਦਾ ਹੋਵੇ, ਜਦੋਂਕਿ ਨਵਾਂ ਫੋਟੌਨ D ਤੱਕ ਗਤੀ ਕਰ ਗਿਆ ਹੋਵੇ। ਇਸ ਗੁੰਝਲਦਾਰ ਪ੍ਰਕ੍ਰਿਆ ਦੀ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਫੇਰ ਤੋਂ ਵਿਅਕਤੀਗਤ ਕਾਰਜਾਂ (ਐਕਸ਼ਨਾਂ): ਤਿੰਨ ਇਲੈਕਟ੍ਰੌਨ ਐਕਸ਼ਨਾਂ, ਦੋ ਫੋਟੌਨ ਐਕਸ਼ਨਾਂ ਅਤੇ ਦੋ ਸ਼ਿਖਰਾਂ- ਇੱਕ ਨਿਕਾਸ ਅਤੇ ਇੱਕ ਸੋਖਣਾ (ਅਬਜ਼ੌਰਪਸ਼ਨ)- ਵਿੱਚੋਂ ਹਰੇਕ ਦੇ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡਾਂ ਨੂੰ ਜਾਣ ਕੇ ਕੈਲਕੁਲੇਟ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ। ਅਸੀਂ ਕੁੱਲ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਉਡ ਨੂੰ ਖੋਜਣ ਦੀ ਉਮੀਦ E ਅਤੇ F ਦੀ ਕਿਸੇ ਵੀ ਚੁਣੀਆਂ ਹੋਈਆਂ ਪੁਜੀਸ਼ਨਾਂ ਲਈ ਹਰੇਕ ਕਾਰਜ (ਐਕਸ਼ਨ) ਦੇ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡਾਂ ਨੂੰ ਗੁਣਾਂ ਕਰਕੇ ਕਰਾਂਗੇ। ਫੇਰ ਅ ਸਾਨੂੰ ਉੱਪਰ ਦਰਸਾਇਆ ਪਹਿਲਾ ਕਨੂੰਨ ਵਰਤ ਕੇ, E ਅਤੇ F ਲਈ ਸਾਰੇ ਬਦਲਵੇਂ ਤਰੀਕਿਆਂ ਲਈ ਇਹਨਾਂ ਸਾਰੇ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡਾਂ ਨੂੰ ਜੋੜਨਾ ਪਏਗਾ। (ਇਹ ਅਭਿਆਸ ਵਿੱਚ ਮੁਢਲਾ ਨਹੀਂ ਹੈ, ਅਤੇ ਇੰਟੀਗ੍ਰੇਸ਼ਨ ਸ਼ਾਮਿਲ ਕਰਦਾ ਹੈ)।
ਪਰ ਇੱਕ ਹੋਰ ਸੰਭਾਵਨਾ ਹੁੰਦੀ ਹੈ, ਜੋ ਇਹ ਹੈ ਕਿ ਇਲੈਕਟ੍ਰੌਨ ਪਹਿਲਾਂ ਤਾਂ G ਤੱਕ ਗਤੀ ਕਰਦਾ ਹੈ, ਜਿੱਥੇ ਇਹ ਇੱਕ ਫੋਟੌਨ ਦਾ ਨਿਕਾਸ ਕਰਦਾ ਹੈ ਜੋ D ਤੱਕ ਜਾਂਦਾ ਹੈ, ਜਦੋਂਕਿ ਇਲੈਕਟ੍ਰੌਨ H ਤੱਕ ਗਤੀ ਕਰਦਾ ਹੈ, ਜਿੱਥੇ ਇਹ ਪਹਿਲੇ ਫੋਟੌਨ ਨੂੰ C ਤੱਕ ਪਹੁੰਚਣ ਤੋਂ ਪਹਿਲਾਂ ਹੀ ਇਸਨੂੰ ਸੋਖ ਲੈਂਦਾ ਹੈ। ਇੱਕ ਵਾਰ ਫੇਰ ਤੋਂ ਅਸੀਂ ਇਹਨਾਂ ਸੰਭਾਵਨਾਵਾਂ (ਸਾਰੇ G ਅਤੇ H ਬਿੰਦੂਆਂ ਲਈ) ਦੇ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡ ਕੈਲਕੁਲੇਟ ਕਰਦੇ ਹਾਂ। ਸਾਡੇ ਕੋਲ ਫੇਰ ਸਾਡੇ ਅਸਲੀ ਸਰਲ ਅਨੁਮਾਨ ਨਾਲੋਂ ਇਹਨਾਂ ਦੋ ਸੰਭਾਵਨਾਂਵਾਂ ਦੇ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡਾਂ ਨੂੰ ਜੋੜ ਕੇ ਬਣੇ ਕੁੱਲ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡ ਦਾ ਇੱਕ ਬੇਹਤਰ ਅਨੁਮਾਨ ਹੁੰਦਾ ਹੈ। ਇੱਤਫਾਕ ਨਾਲ ਇੱਕ ਫੋਟੌਨ ਦੀ ਇੱਕ ਇਲੈਕਟ੍ਰੌਨ ਨਾਲ ਇੱਸ ਤਰਾਂ ਦੀ ਇਸ ਪਰਸਪਰ ਕ੍ਰਿਆ ਨੂੰ ਕੌਂਪਟਨ ਸਕੈਟ੍ਰਿੰਗ ਦਾ ਨਾਮ ਦਿੱਤਾ ਗਿਆ ਹੈ।
ਹੋਰ ਮੱਧ ਪ੍ਰਕ੍ਰਿਆਵਾਂ ਦੀ ਅਜਿਹੀ ਬਹੁਗਿਣਤੀ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿੱਚ ਹੋਰ ਅਤੇ ਹੋਰ ਜਿਆਦਾ ਫੋਟੌਨ ਸੌਖੇ ਅਤੇ/ਜਾਂ ਨਿਕਾਸੇ ਜਾਂਦੇ ਹਨ। ਇਹਨਾਂ ਸਾਰੀਆਂ ਸੰਭਾਵਨਾਵਾਂ ਵਿੱਚੋਂ ਹਰੇਕ ਸੰਭਾਵਨਾ ਲਈ ਇਸ ਨੂੰ ਦਰਸਾਉਣ ਵਾਲਾ ਇੱਕ ਫੇਨਮੈਨ ਚਿੱਤਰ ਹੁੰਦਾ ਹੈ। ਇਹ ਨਤੀਜਨ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡਾਂ ਲਈ ਇੱਕ ਗੁੰਝਲਦਾਰ ਹਿਸਾਨ ਕਿਤਾਬ ਦਰਸਾਉਂਦਾ ਹੈ, ਪਰ ਇਸ ਗੱਲ ਦੇ ਦਿੱਤੇ ਹੋਣ ਤੇ ਕਿ ਇਹ ਇੱਕ ਅਜਿਹਾ ਮਾਮਲਾ ਹੈ ਜਿਸ ਵਿੱਚ ਚਿੱਤਰ ਜਿੰਨਾ ਗੁੰਝਲਦਾਰ ਹੋਵੇਗਾ ਉੰਨਾ ਹੀ ਘੱਟ ਇਹ ਨਤੀਜੇ ਵਿੱਚ ਯੋਗਦਾਨ ਦੇਵੇਗਾ, ਇਹ ਸਿਰਫ ਮੂਲ ਸਵਾਲ ਜਿੰਨਾ ਸ਼ੁੱਧ ਜਵਾਬ ਖੋਜਣ ਲਈ ਇੱਕ ਵਕਤ ਅਤੇ ਯਤਨ ਦਾ ਮਸਲਾ ਹੁੰਦਾ ਹੈ। ਇਹ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਦੀ ਬੁਨਿਆਦੀ ਪਹੁੰਚ ਹੈ। ਇਲੈਕਟ੍ਰੌਨਾਂ ਅਤੇ ਫੋਟੌਨਾਂ ਦਰਮਿਆਨ ਕਿਸੇ ਵੀ ਪਰਸਪਰ ਕ੍ਰਿਆ ਦੀ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਕੈਲਕੁਲੇਟ ਕਰਨ ਲਈ ਇਹ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਫੇਨਮੈਨ ਚਿੱਤਰਾਂ ਵਿੱਚ ਉਹ ਸਾਰੇ ਸੰਭਵ ਤਰੀਕੇ ਨੋਟ ਕਰਨ ਦਾ ਮਸਲਾ ਹੈ ਜਿਹਨਾਂ ਵਿੱਚ ਤਿੰਨ ਬੁਨਿਆਦੀ ਤੱਤਾਂ ਤੋਂ ਕ੍ਰਿਆ ਨੂੰ ਰਚਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਹਰੇਕ ਚਿੱਤਰ ਸਬੰਧਤ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡ ਖੋਜਣ ਲਈ ਨਿਸ਼ਚਿਤ ਕਨੂੰਨਾਂ ਵਾਲੇ ਕੁੱਝ ਹਿਸਾਬ ਕਿਤਾਬ ਵਾਲਾ ਹੁੰਦਾ ਹੈ।
ਇਹ ਬੁਨਿਆਦੀ ਕੱਚਾ ਢਾਂਚਾ ਬਣਿਆ ਰਹਿੰਦਾ ਹੈ ਜਦੋਂ ਕੋਈ ਇੱਕ ਕੁਆਂਟਮ ਵਿਵਰਣ ਤੱਕ ਗਤੀ ਕਰਦਾ ਹੈ ਪਰ ਕੁੱਝ ਸੰਕਲਪਿਕ ਤਬਦੀਲੀਆਂ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ। ਇੱਕ ਲੋੜ ਇਹ ਪੈਂਦੀ ਹੈ ਕਿ ਜਿੱਥੇ ਸਾਨੂੰ ਰੋਜ਼ਾਨਾ ਜਿੰਦਗੀ ਵਿੱਚ ਇਹ ਉਮੀਦ ਰੱਖਣੀ ਚਾਹੀਦੀ ਹੈ ਕਿ ਬਿੰਦੂਆਂ ਉੱਤੇ ਕੁੱਝ ਰੁਕਾਵਟਾਂ ਹੋ ਸਕਦੀਆਂ ਹੋਣਗੀਆਂ ਜਿਹਨਾਂ ਤੱਕ ਕੋਈ ਕਣ ਗਤੀ ਕਰ ਸਕਦਾ ਹੈ, ਇਹ ਪੂਰੇ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਵਿੱਚ ਸੱਚ ਨਹੀਂ ਹੈ। ਕਿਸੇ ਇਲੈਕਟ੍ਰੌਨ ਦੀ A ਉੱਤੇ, ਜਾਂ ਇੱਕ ਫੋਟੌਨ ਦੀ B ਉੱਤੇ, ਇੱਕ ਸੰਭਾਵਨਾ ਹੁੰਦੀ ਹੈ, ਜੋ ਬ੍ਰਹਿਮੰਡ ਵਿੱਚ ਕਿਸੇ ਹੋਰ ਸਥਾਨ ਅਤੇ ਵਕਤ ਤੱਕ ਇੱਕ ਮੁਢਲੇ ਕਾਰਜ ਦੇ ਤੌਰ ਤੇ ਗਤੀ ਕਰ ਰਿਹਾ ਹੁੰਦਾ ਹੈ। ਇਸ ਵਿੱਚ ਉਹ ਸਥਾਨ ਵੀ ਸ਼ਾਮਿਲ ਹੁੰਦੇ ਹਨ ਜੋ ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਤੋਂ ਜਿਆਦਾ ਸਪੀਡ ਉੱਤੇ ਹੀ ਪਹੁੰਚਣਯੋਗ ਹੁੰਦੇ ਹਨ ਅਤੇ ਵਕਤ ਤੋਂ ਪਹਿਲਾਂ ਪਹੁੰਚਣ ਵਾਲੇ ਸਥਾਨ ਵੀ ਹੁੰਦੇ ਹਨ। (ਵਕਤ ਵਿੱਚ ਪਿੱਛੇ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਗਤੀਸ਼ੀਲ ਇੱਕ ਇਲੈਕਟ੍ਰੌਨ ਵਕਤ ਵਿੱਚ ਅੱਗੇ ਵੱਲ ਨੂੰ ਗਤੀਸ਼ੀਲ ਕਿਸੇ ਪੌਜ਼ੀਟ੍ਰੌਨ ਦੇ ਤੌਰ ਤੇ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ)
ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡ
[ਸੋਧੋ]
ਕੁਆਂਟਮ ਮਕੈਨਿਕਸ ਖੋਜਯੋਗਤਾਵਾਂ (ਪ੍ਰੋਬੇਬਿਲਟੀਆਂ) ਦਾ ਪਤਾ ਲਗਾਉਣ ਦੇ ਤਰੀਕੇ ਵਿੱਚ ਇੱਕ ਮਹੱਤਵਪੂਰਨ ਤਬਦੀਲੀ ਪੇਸ਼ ਕਰਦਾ ਹੈ। ਪ੍ਰੋਬੇਬਿਲਟੀਆਂ ਅਜੇ ਵੀ ਸਾਡੀ ਰੋਜ਼ਾਨਾ ਸੰਸਾਰ ਵਿੱਚ ਸਾਡੇ ਦੁਆਰਾ ਵਰਤੀਆਂ ਜਾਣ ਵਾਲੇ ਪ੍ਰੋਬੇਬਿਲਟੀਆਂ ਲਈ ਆਮ ਵਾਸਤਵਿਕ ਨੰਬਰਾਂ ਦੁਆਰਾ ਪ੍ਰਸਤੁਤ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ, ਪਰ ਪ੍ਰੋਬੇਬਿਲਟੀਆਂ ਨੂੰ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡਾਂ ਦੇ ਵਰਗ (ਸਕੁਏਅਰ) ਦੇ ਤੌਰ ਤੇ ਪਤਾ ਲਗਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ। ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡ ਕੰਪਲੈਕਸ ਨੰਬਰ ਹੁੰਦੇ ਹਨ।
ਫੇਨਮੈਨ ਕਿਸੇ ਕਾਗਜ਼ ਦੇ ਟੁਕੜੇ ਜਾਂ ਸਕਰੀਨ ਉੱਤੇ ਤੀਰਾਂ ਦੇ ਤੌਰ ਤੇ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਨੂੰ ਇੱਕ ਸਰਲ ਪਰ ਸ਼ੁੱਧ ਤਰੀਕਾ ਵਰਤਕੇ ਪ੍ਰਸਤੁਤ ਕਰਕੇ ਪਾਠਕਾਂ ਅੱਗੇ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੀ ਪ੍ਰਦ੍ਰਸ਼ਨੀ ਤੋਂ ਗੁਰੇਜ਼ ਕਰਦਾ ਹੈ। (ਇਹਨਾਂ ਨੂੰ ਫੇਨਮੈਨ ਚਿੱਤਰਾਂ ਦੇ ਤੀਰ ਨਹੀਂ ਸਮਝਣਾ ਚਾਹੀਦਾ ਜੋ ਸੱਚਮੁੱਚ ਸਪੇਸ ਦੀਆਂ ਤਿੰਨ ਡਾਇਮੈਨਸ਼ਨਾਂ ਅਤੇ ਇੱਕ ਵਕਤ ਦੇ ਅਯਾਮ ਵਿੱਚ ਬਿੰਦੂਆਂ ਦਰਮਿਆਨ ਇੱਕ ਸਬੰਧ ਵਾਲੀਆਂ ਦੋ ਡਾਇਮੈਨਸ਼ਨਾਂ ਵਿੱਚ ਸਰਲ ਕੀਤੀਆਂ ਗਈਆਂ ਪ੍ਰਸਤੁਤੀਆਂ ਹਨ)। ਐਂਪਲੀਟਿਊਡ ਤੀਰ ਕੁਆਂਟਮ ਥਿਊਰੀ ਦੁਆਰਾ ਦਿੱਤੇ ਜਾਂਦੇ ਸੰਸਾਰ ਦੇ ਵਿਵਰਣ ਲਈ ਬੁਨਿਆਦੀ ਹਨ। ਇਹਨਾਂ ਦੀ ਜਰੂਰਤ ਲਈ ਕੋਈ ਸੰਤੁਸ਼ਟੀਜਨਕ ਕਾਰਣ ਨਹੀਂ ਦਿੱਤਾ ਗਿਆ ਹੈ। ਪਰ ਵਿਵਹਾਰਿਕ ਤੌਰ ਤੇ ਸਾਨੂੰ ਇਹ ਸਵੀਕਾਰ ਕਰਨਾ ਹੀ ਪੈਂਦਾ ਹੈ ਕਿ ਇਹ ਸਾਰੇ ਕੁਆਂਟਮ ਘਟਨਾਕ੍ਰਮ ਦੇ ਸਾਡੇ ਵਿਚਰਣ ਦਾ ਇੱਕ ਲਾਜ਼ਮੀ ਹਿੱਸਾ ਹਨ।
ਇਹ ਇਸ ਸਰਲ ਕਨੂੰਨ ਦੁਆਰਾ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਦੇ ਸਾਡੇ ਰੋਜ਼ਾਨਾ ਵਿਚਾਰਾਂ ਨਾਲ ਸਬੰਧਤ ਹੈ ਕਿ ਕਿਸੇ ਘਟਨਾ ਦੀ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਸਬੰਧਤ ਐਂਪਲੀਟਿਊਡ ਤੀਰ ਦੀ ਲੰਬਾਈ ਦਾ ਵਰਗ ਹੁੰਦਾ ਹੈ। ਇਸਲਈ, ਕਿਸੇ ਦਿੱਤੀ ਹੋਈ ਪ੍ਰਕ੍ਰਿਆ ਲਈ, ਜੇਕਰ ਦੋ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡ v ਅਤੇ w ਸ਼ਾਮਿਲ ਹੁੰਦੇ ਹੋਣ, ਤਾਂ ਪ੍ਰਕ੍ਰਿਆ ਦੀ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਇਹਨਾਂ ਦੋ ਸਮੀਕਰਨਾਂ ਵਿੱਚੋਂ ਕਿਸੇ ਇੱਕ ਸਮੀਕਰਨ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾਂਦੀ ਹੈ:
ਜਾਂ
ਕਨੂੰਨ ਜਿਵੇਂ ਜੋੜਨਾ ਜਾਂ ਗੁਣਾ ਕਰਨਾ ਕਹੇ ਜਾਂਦੇ ਹਨ, ਫੇਰ ਵੀ, ਉੱਪਰ ਦੱਸੇ ਮੁਤਾਬਿਕ ਉਹੀ ਹੁੰਦੇ ਹਨ। ਪਰ ਜਿੱਥੇ ਤੁਸੀਂ ਖੋਜਯੋਗਤਾਵਾਂ (ਪ੍ਰੋਬੇਬਿਲਟੀਆਂ) ਨੂੰ ਜੋੜਨ ਜਾਂ ਗੁਣਾ ਕਰਨ ਦੀ ਉਮੀਦ ਕਰਦੇ ਹੋ, ਉੱਥੇ ਤੁਸੀਂ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡਾਂ ਨੂੰ ਜੋੜਨ ਜਾਂ ਗੁਣਾ ਕਰਦੇ ਹੋ ਜੋ ਹੁਣ ਕੰਪਲੈਕਸ ਨੰਬਰ ਹੁੰਦੇ ਹਨ।

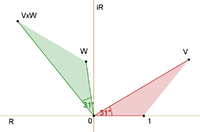
ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੀ ਥਿਊਰੀ ਵਿੱਚ ਜੋੜਫਲ ਅਤੇ ਗੁਣਨਫਲ ਪ੍ਰਾਪਤ ਕਰਨਾ ਜਾਣੇ ਪਛਾਣੇ ਓਪਰੇਸ਼ਨ ਹਨ ਅਤੇ ਤਸਵੀਰਾਂ ਵਿੱਚ ਦਿਖਾਏ ਗਏ ਹਨ। ਜੋੜ ਇਸਤਰਾਂ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਦੂਜੇ ਤੀਰ ਨੂੰ ਪਹਿਲੇ ਦੇ ਅੰਤ ਉੱਤੇ ਸ਼ੁਰੂ ਹੋਣ ਦਿਓ। ਜੋੜ ਫੇਰ ਇੱਕ ਤੀਜਾ ਤੀਰ ਹੁੰਦਾ ਹੈ ਜੋ ਸਿੱਧਾ ਹੀ ਦੂਜੇ ਦੇ ਅੰਤ ਤੱਕ ਪਹਿਲੇ ਤੋਂ ਸ਼ੁਰੂ ਹੋ ਕੇ ਜਾਂਦਾ ਹੈ। ਦੋਵੇਂ ਤੀਰਾਂ ਦਾ ਗੁਣਨਫਲ ਇੱਕ ਅਜਿਹਾ ਤੀਰ ਹੁੰਦਾ ਹੈ ਜਿਸਦੀ ਲੰਬਾਈ ਦੋਵੇਂ ਲੰਬਾਈਆਂ ਦਾ ਗੁਣਨਫਲ ਹੁੰਦੀ ਹੈ। ਗੁਣਨਫਲ ਦੀ ਦਿਸ਼ਾ ਉਹਨਾਂ ਐਂਗਲਾਂ ਨੂੰ ਜੋੜ ਕੇ ਖੋਜੀ ਜਾਂਦੀ ਹੈ ਜਿਹਨਾਂ ਰਾਹੀਂ ਕਿਸੇ ਰੈੱਫਰੈਂਸ ਦਿਸ਼ਾ ਦੇ ਸਾਪੇਖਿਕ ਦੋਵਾਂ ਨੂੰ ਘੁਮਾਇਆ ਜਾਂਦਾ ਹੈ: ਜੋ ਉਹ ਐਂਗਲ ਦਿੰਦਾ ਹੈ ਜਿਸ ਰਾਹੀਂ ਗੁਣਨਫਲ ਨੂੰ ਰੈੱਫਰੈਂਸ ਦਿਸ਼ਾ ਦੇ ਸਾਪੇਖਿਕ ਘੁਮਾਇਆ ਜਾਂਦਾ ਹੈ।
ਪ੍ਰੋਬੇਬਿਲਟੀਆਂ ਤੋਂ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡਾਂ ਤੱਕ ਦੀ ਇਹ ਤਬਦੀਲੀ, ਬੁਨਿਆਦੀ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਬਦਲੇ ਬਗੈਰ ਹੀ ਗਣਿਤ ਨੂੰ ਗੁੰਝਲਦਾਰ ਬਣਾਉਂਦੀ ਹੈ। ਪਰ ਇਹ ਤਬਦੀਲੀ ਅਜੇ ਵੀ ਕਾਫੀ ਨਹੀਂ ਹੁੰਦੀ ਕਿਉਂਕਿ ਇਹ ਇਸ ਤੱਥ ਨੂੰ ਲੈਣ ਵਿੱਚ ਅਸਫਲ ਰਹਿੰਦੀ ਹੈ ਕਿ ਫੋਟੌਨਾਂ ਅਤੇ ਇਲੈਕਟ੍ਰੌਨਾਂ ਦੋਵਾਂ ਨੂੰ ਹੀ ਪੋਲਰਾਈਜ਼ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਜਿਸਦਾ ਕਹਿਣ ਦਾ ਅਰਥ ਹੈ ਕਿ ਸਪੇਸ ਅਤੇ ਸਮੇਂ ਵਿੱਚ ਇਹਨਾਂ ਦੀਆਂ ਦਿਸ਼ਾਵਾਂ ਦਾ ਲਟਕਾਓ ਵੀ ਲੈਣਾ ਪੈਂਦਾ ਹੈ। ਇਸਲਈ, P(A ਤੋਂ B) ਅਸਲ ਵਿੱਚ 16 ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਜਾਂ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡਾਂ ਦੀ ਬਣੀ ਹੁੰਦੀ ਹੈ। ਮਾਤਰਾ “j” ਨਾਲ ਵੀ ਕੁੱਝ ਸੂਖਮ ਤਬਦੀਲੀਆਂ ਹੁੰਦੀਆਂ ਹਨ, ਜਿਸਨੂੰ ਕੁੱਝ ਪੋਲਰਾਇਜ਼ੇਸ਼ਨਾਂ ਲਈ 90 ਡਿਗਰੀ ਦੇ ਗੁਣਾਂਕ ਵਿੱਚ ਘੁਮਾਇਆ ਜਾਣਾ ਪੈ ਸਕਦਾ ਹੈ, ਜੋ ਵਿਸਥਾਰਪੂਰਵਕ ਰਿਕਾਰਡ ਰੱਖਣ ਲਈ ਇੱਕੋ ਇੱਕ ਦਿਲਚਸਪ ਚੀਜ਼ ਹੈ।
ਇਸ ਤੱਥ ਨਾਲ ਸਬੰਧਤ ਕਿ ਇਲੈਕਟ੍ਰੌਨ ਨੂੰ ਪੋਲਰਾਇਜ਼ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਇੱਕ ਹੋਰ ਛੋਟਾ ਲਾਜ਼ਮੀ ਵਿਵਰਣ ਹੈ ਜੋ ਇਸ ਤੱਥ ਨਾਲ ਜੁੜਿਆ ਹੁੰਦਾ ਹੈ ਕਿ ਇੱਕ ਇਲੈਕਟ੍ਰੌਨ ਇੱਕ ਫਰਮੀਔਨ ਹੁੰਦਾ ਹੈ ਅਤੇ ਫਰਮੀ-ਡੀਰਾਕ ਸਟੈਟਿਸਟਿਕਸ ਦੀ ਪਾਲਣਾ ਕਰਦਾ ਹੈ। ਬੁਨਿਆਦੀ ਕਨੂੰਨ ਇਹ ਹੈ ਕਿ ਜੇਕਰ ਸਾਡੇ ਕੋਲ ਇੱਕ ਇਲੈਕਟ੍ਰੌਨ ਤੋਂ ਜਿਆਦਾ ਇਲੈਕਟ੍ਰੌਨਾਂ ਵਾਲੀ ਕਿਸੇ ਦਿੱਤੀ ਹੋਈ ਕੰਪਲੈਕਸ ਪ੍ਰਕ੍ਰਿਆ ਲਈ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡ ਹੋਣ, ਤਾਂ ਜਦੋਂ ਅਸੀਂ ਪੂਰਕ ਫੇਨਮੈਨ ਚਿੱਤਰ ਸ਼ਾਮਿਲ ਕਰਦੇ ਹਾਂ (ਜੋ ਸਾਨੂੰ ਹਮੇਸ਼ਾਂ ਹੀ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ) ਜਿਹਨਾਂ ਵਿੱਚ ਅਸੀਂ ਸਿਰਫ ਦੋ ਇਲੈਕਟ੍ਰੌਨ ਘਟਨਾਵਾਂ ਦਾ ਹੀ ਵਟਾਂਦਰਾ ਕਰਦੇ ਹਾਂ, ਨਤੀਜਨ ਐਂਪਲੀਟਿਊਡ ਪਹਿਲੇ ਦਾ ਨੈਗਟਿਵ- ਉਲਟਾ ਹੁੰਦਾ ਹੈ। ਸਰਲਤਮ ਮਾਮਲਾ A ਅਤੇ B ਤੋਂ ਸ਼ੁਰੂ ਹੋ ਕੇ C ਅਤੇ D ਉੱਤੇ ਮੁੱਕਣ ਵਾਲੇ ਦੋ ਇਲੈਕਟ੍ਰੌਨਾਂ ਵਾਲਾ ਹੁੰਦਾ ਹੈ। ਐਂਪਲੀਟਿਊਡ ਦਾ ਹਿਸਾਬ “ਅੰਤਰ”, E(A ਤੋਂ D) × E(B ਤੋਂ C) − E(A ਤੋਂ C) × E(B ਤੋਂ D) ਦੇ ਰੂਪ ਵਿੱਚ ਲਗਾਇਆ ਜਾਂਦਾ ਹੈ , ਜਿੱਥੇ ਅਸੀਂ ਪ੍ਰੋਬੇਬਿਲਟੀਆਂ ਦੇ ਅਪਣੇ ਰੋਜ਼ਾਨਾ ਵਿਚਾਰਾਂ ਤੋਂ ਉਮੀਦ ਕਰਦੇ ਹਾਂ ਕਿ ਇਹ ਇੱਕ ਜੋੜ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ।
ਪ੍ਰਸਾਰਕ
[ਸੋਧੋ]ਅੰਤ ਵਿੱਚ, ਫੋਟੌਨ ਅਤੇ ਇਲੈਕਟ੍ਰੌਨ ਲਈ ਕ੍ਰਮਵਾਰ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡਾਂ ਨਾਲ ਸਬੰਧਤ P (A ਤੋਂ B) ਅਤੇ E (C ਤੋਂ D) ਦਾ ਹਿਸਾਬ ਲਗਾਉਣਾ ਹੁੰਦਾ ਹੈ। ਇਹ ਲਾਜ਼ਮੀ ਤੌਰ ਤੇ ਡੀਰਾਕ ਇਕੁਏਸ਼ਨ ਦੇ ਹੱਲ ਹੁੰਦੇ ਹਨ ਜੋ ਇਲੈਕਟ੍ਰੌਨ ਦੇ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡ ਦਾ ਵਰਤਾਓ ਦਰਸਾਉਂਦੇ ਹਨ ਅਤੇ ਕਲੇਇਨ-ਜੌਰਡਨ ਇਕੁਏਸ਼ਨ ਦੇ ਹੱਲ ਹੁੰਦੇ ਹਨ ਜੋ ਫੋਟੌਨ ਦੇ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡ ਦਾ ਵਰਤਾਓ ਦਰਸਾਉਂਦੇ ਹਨ। ਇਹਨਾਂ ਨੂੰ ਫੇਨਮੈਨ ਪ੍ਰੌਪੇਗੇਟਰ (ਪ੍ਰਸਾਰਕ) ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਮਿਆਰੀ ਸਾਹਿਤ ਵਿੱਚ ਸਾਂਝੇ ਤੌਰ ਤੇ ਵਰਤੀ ਜਾਂਦੀ ਇੱਕ ਧਾਰਨਾ ਦਾ ਬਦਲ ਇਸਤਰਾਂ ਹੈ:
ਜਿੱਥੇ ਵਰਗਾ ਇੱਕ ਸੰਖੇਪ ਸੰਕੇਤ ਚਿੰਨ ਚਾਰ ਵਾਸਤਵਿਕ ਨੰਬਰਾਂ ਲਈ ਹੁੰਦਾ ਹੈ ਜੋ A ਨਾਮਕ ਬਿੰਦੂ ਦਾ ਤਿੰਨ ਅਯਾਮਾਂ ਵਿੱਚ ਪੁਜ਼ੀਸ਼ਨ ਅਤੇ ਵਕਤ ਦਿੰਦੇ ਹਨ।
ਪੁੰਜ ਪੁਨਰ-ਮਾਨਕੀਕਰਨ
[ਸੋਧੋ]
ਇੱਕ ਸਮੱਸਿਆ ਇਤਿਹਾਸਿਕ ਤੌਰ ਤੇ ਪੈਦਾ ਹੋਈ ਜਿਸਨੇ ਵੀਹ ਸਾਲਾਂ ਤੱਕ ਅੱਗੇ ਤਰੱਕੀ ਰੋਕੀਂ ਰੱਖੀ: ਭਾਵੇਂ ਅਸੀਂ ਤਿੰਨ ਬੁਨਿਆਦੀ “ਸਰਲ” ਐਕਸ਼ਨਾਂ ਦੀ ਮਾਨਤਾ ਨਾਲ ਸ਼ੁਰੂ ਕਰਦੇ ਹਾਂ, ਖੇਡ ਦੇ ਕਨੂੰਨ ਕਹਿੰਦੇ ਹਨ ਕਿ ਜੇਕਰ ਅਸੀਂ ਇੱਕ ਇਲੈਕਟ੍ਰੌਨ ਦੇ A ਤੋਂ B ਤੱਕ ਜਾਣ ਵਾਸਤੇ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡ ਕੈਲਕੁਲੇਟ ਕਰਦੇ ਹਾਂ ਤਾਂ ਸਾਨੂੰ ਸਾਰੇ ਸੰਭਵ ਰਸਤੇ ਹਿਸਾਬ ਕਿਤਾਬ ਅੰਦਰ ਵਿਚਾਰਨੇ ਪੈਣਗੇ: ਉਹਨਾਂ ਅੰਤਿਮ ਸਿਰਿਆਂ ਵਾਲੇ ਬਿੰਦੂਆਂ ਵਾਲੇ ਸਾਰੇ ਸੰਭਵ ਫੇਨਮੈਨ ਚਿੱਤਰ। ਇਸ ਕਾਰਣ ਇੱਕ ਅਜਿਹਾ ਰਸਤਾ ਹੋਵੇਗਾ ਜਿਸ ਵਿੱਚ ਇਲੈਕਟ੍ਰੌਨ C ਤੱਕ ਯਾਤਰਾ ਕਰਦਾ ਹੋਵੇਗਾ, ਉੱਥੇ ਇੱਕ ਫੋਟੋਨ ਬਾਹਰ ਕੱਢਦਾ ਹੋਵੇਗਾ ਅਤੇ ਫੇਰ ਇਸਨੂੰ B ਤੱਕ ਪਹੁੰਚਣ ਤੋਂ ਪਹਿਲਾਂ ਹੀ ਦੁਬਾਰਾ ਸੋਖ ਲੈਂਦਾ ਹੋਵੇਗਾ। ਜਾਂ ਇਸ ਕਿਸਮ ਦੀ ਚੀਜ਼ ਨੂੰ ਦੋ ਵਾਰ ਕਰਦਾ ਹੋ ਸਕਦਾ ਹੋਵੇਗਾ, ਜਾਂ ਜਿਆਦਾ ਵਾਰ ਵੀ। ਸੰਖੇਪ ਵਿੱਚ, ਸਾਡੇ ਕੋਲ ਇੱਕ ਭਿੰਨ-ਵਰਗੀ ਪ੍ਰਸਥਿਤੀ ਪੈਦਾ ਹੋ ਜਾਂਦੀ ਹੈ ਜਿਸ ਵਿੱਚ ਜੇਕਰ ਅਸੀਂ ਕਿਸੇ ਰੇਖਾ ਉੱਤੇ ਨਜ਼ਦੀਕ ਤੋਂ ਨਜ਼ਰ ਪਾਈਏ ਤਾਂ ਇਹ “ਸਰਲ” ਰੇਖਾਵਾਂ ਦੇ ਸਮੂਹ ਵਿੱਚ ਟੁੱਟੀ ਨਜ਼ਰ ਆਉਂਦੀ ਹੈ, ਜਿਹਨਾਂ ਵਿੱਚੋਂ ਹਰੇਕ ਰੇਖਾ, ਜੇਕਰ ਨਜ਼ਦੀਕ ਤੋਂ ਦੇਖੀ ਜਾਵੇ, ਤਾਂ ਬਦਲੇ ਵਿੱਚ ਹੋਰ “ਸਰਲ” ਰੇਖਾਵਾਂ ਤੋਂ ਬਣੀ ਨਜ਼ਰ ਆਉਂਦੀ ਹੈ, ਅਤੇ ਅਸੀਮ ਰੂਪ ਵਿੱਚ ਹੋਰ ਅੱਗੇ ਇਸੇ ਤਰਾਂ ਹੁੰਦਾ ਜਾਂਦਾ ਹੈ। ਇਹ ਸੰਭਾਲਨ ਲਈ ਕਾਫੀ ਕਠਿਨ ਪ੍ਰਸਥਿਤੀ ਹੁੰਦੀ ਹੈ। ਜੇਕਰ ਇਸ ਵਿਵਰਣ ਨੂੰ ਜੋੜਨ ਨਾਲ ਚੀਜ਼ਾਂ ਜਰਾ ਜਿੰਨੀਆਂ ਹੀ ਬਦਲਦੀਆਂ ਹਨ ਤਾਂ ਇੰਨੀ ਜਿਆਦਾ ਬੁਰੀ ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ ਸੀ, ਪਰ ਬਦਕਿਸਮਤੀ ਉਦੋਂ ਹੋਈ ਜਦੋਂ ਇਹ ਖੋਜਿਆ ਗਿਆ ਕਿ ਉੱਪਰ ਦੱਸੀ ਸਰਲ ਸੋਧ ਨੇ ਅਨੰਤ ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡਾਂ ਵੱਲ ਮਜਬੂਰ ਕੀਤਾ। ਓਸ ਵਕਤ ਇਹ ਸਮੱਸਿਆ ਪੁਨਰਮਾਨਕੀਕਰਨ ਦੀ ਤਕਨੀਕ ਰਾਹੀਂ ਸੁਲਝਾ ਦਿੱਤੀ ਗਈ। ਫੇਰ ਵੀ, ਫੇਨਮੈਨ ਖੁਸ ਇਸ ਬਾਰੇ ਨਾਖੁਸ਼ ਰਿਹਾ, ਤੇ ਇਸਨੂੰ ਉਸਨੇ ਇੱਕ “ਪਾਗਲ ਵਿਧੀ” ਕਿਹਾ।
ਪਰਿਣਾਮ
[ਸੋਧੋ]ਉੱਪਰ ਦਰਸਾਏ ਢਾਂਚੇ ਅੰਦਰ ਭੌਤਿਕ ਵਿਗਿਆਨੀ ਫੇਰ ਅਸੰਗਤ ਚੁੰਬਕੀ ਡਾਇਪੋਲ ਮੋਮੈਂਟ ਵਰਗੀਆਂ ਇਲੈਕਟ੍ਰੌਨਾਂ ਦੀਆਂ ਕੁੱਝ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਨੂੰ ਉੱਚ ਸ਼ੁੱਧਤਾ ਦੀ ਡਿਗਰੀ ਤੱਕ ਕੈਲਕੁਲੇਟ ਕਰਨ ਦੇ ਯੋਗ ਰਹੇ ਸਨ। ਫੇਰ ਵੀ, ਜਿਵੇਂ ਫੇਨਮੈਨ ਨੇ ਇਸ਼ਾਰਾ ਕੀਤਾ, ਇਹ ਕੁੱਲ ਮਿਲਾ ਕੇ ਇਹ ਸਮਝਾਉਣ ਵਿੱਚ ਅਸਫਲ ਰਹੀ ਕਿ ਇਲੈਕਟ੍ਰੌਨਾਂ ਵਰਗੇ ਕਣ ਪੁੰਜ ਕਿਉਂ ਰੱਖਦੇ ਹਨ। “ਕੋਈ ਅਜਿਹੀ ਥਿਊਰਿ ਨਹੀਂ ਹੈ ਜੋ ਜਰੂਰੀ ਮਾਤਰਾ ਵਿੱਚ ਇਹਨਾਂ ਨੰਬਰਾਂ ਬਾਰੇ ਸਮਝਾ ਸਕਦੀ ਹੋਵੇ। ਅਸੀਂ ਅਪਣੀਆਂ ਸਭ ਥਿਊਰੀਆਂ ਵਿੱਚ ਨੰਬਰ ਵਰਤਦੇ ਹਾਂ, ਪਰ ਅਸੀਂ ਉਹਨਾਂ ਨੂੰ ਨਹੀਂ ਸਮਝਦੇ- ਉਹ ਕੀ ਹਨ, ਜਾਂ ਉਹ ਕਿੱਥੋਂ ਆਏ ਹਨ। ਮੈਂ ਮੰਨਦਾ ਹਾਂ ਕਿ ਇੱਕ ਬੁਨਿਆਦੀ ਨਜ਼ਰੀਏ ਤੋਂ, ਇਹ ਬਹੁਤ ਹੀ ਦਿਲਚਸਪ ਅਤੇ ਗੰਭੀਰ ਸਮੱਸਿਆ ਹੈ। ”
ਗਣਿਤ
[ਸੋਧੋ]ਗਣਿਤਿਕ ਤੌਰ ਤੇ, ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ U(1) ਸਮਿੱਟਰੀ ਗਰੁੱਪ ਵਾਲੀ ਇੱਕ ਅਬੇਲੀਅਨ ਗੇਜ ਥਿਊਰੀ ਹੈ। ਗੇਜ ਫੀਲਡ ਜੋ ਚਾਰਜ ਕੀਤੀਆਂ ਹੋਈਆਂ ਸਪਿੱਨ-½ ਫੀਲਡਾਂ ਦਰਮਿਆਨ ਪਰਸਪਰ ਕ੍ਰਿਆ ਦੀ ਵਿਚੋਲਗਿਰੀ ਕਰਦੀ ਹੈ, ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਫੀਲਡ ਹੁੰਦੀ ਹੈ। ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਫੀਲਡ ਨਾਲ ਪਰਸਪਰ ਕ੍ਰਿਆ ਕਰਨ ਵਾਲੀ ਸਪਿੱਨ-½ ਫੀਲਡ ਲਈ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਲਗਰਾਂਜੀਅਨ ਇਸ ਹੇਠਾਂ ਲਿਖੀ ਸਮੀਕਰਨ ਦੇ ਵਾਸਤਵਿਕ ਹਿੱਸੇ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ,
ਜਿੱਥੇ
- ਡੀਰਾਕ ਮੈਟ੍ਰੀਸੀਜ਼ ਹਨ;
- ਸਪਿੱਨ-½ ਕਣਾਂ ਦੀ ਬਾਇਸਪਿੱਨੌਰ ਫੀਲਡ ਹੈ (ਯਾਨਿ ਕਿ ਇਲੈਕਟ੍ਰੌਨ-ਪੌਜ਼ੀਟ੍ਰੌਨ ਫੀਲਡ);
- , ਨੂੰ "ਸਾਈ-ਬਾਰ" ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਜਿਸਨੂੰ ਕਦੇ ਕਦੇ ਡੀਰਾਕ ਅਡਜੋਆਇੰਟ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ;
- ਗੇਜ ਕੋਵੇਰੀਅੰਟ ਡੈਰੀਵੇਟਿਵ ਹੈ;
- e ਕਪਲਿੰਗ ਸਥਿਰਾਂਕ ਹੈ, ਜੋ ਬਾਇਸਪਿੱਨੌਰ ਫੀਲਡ ਦੇ ਇਲੈਕਟ੍ਰਿਕ ਚਾਰਜ ਬਰਾਬਰ ਹੈ;
- m ਇਲੈਕਟ੍ਰੌਨ ਜਾਂ ਪੌਜ਼ੀਟ੍ਰੌਨ ਦਾ ਪੁੰਜ ਹੈ;
- ਖੁਦ ਇਲੈਕਟ੍ਰੌਨ ਦੁਆਰਾ ਪੈਦਾ ਕੀਤੀ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਫੀਲਡ ਦਾ ਕੋਵੇਰੀਅੰਟ ਫੋਰ-ਪੁਟੈਂਸ਼ਲ ਹੈ;
- ਬਾਹਰੀ ਸੋਮੇ ਦੁਆਰਾ ਥੋਪੀ ਗਈ ਬਾਹਰੀ ਫੀਲਡ ਹੈ;
- ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਫੀਲਡ ਟੈਂਸਰ ਹੈ।
ਗਤੀ ਦੀਆਂ ਸਮੀਕਰਨਾਂ
[ਸੋਧੋ]ਸ਼ੁਰੂਆਤ ਲਈ, ਲਗਰਾਂਜੀਅਨ ਵਿੱਚ D ਦੀ ਪਰਿਭਾਸ਼ਾ ਭਰਦੇ ਹੋਏ ਸਾਨੂੰ ਇਹ ਮਿਲਦਾ ਹੈ,
ਇਸਤੋਂ ਬਾਦ, ਅਸੀਂ ਲਗਰਾਂਜੀਅਨ ਨੂੰ ਕਿਸੇ ਫੀਲਡ ਲਈ ਗਤੀ ਦੀ ਇਲੁਰ-ਲਗਰਾਂਜੀਅਨ ਸਮੀਕਰਨ ਵਿੱਚ ਭਰਦੇ ਹਾਂ, ਤਾਂ ਜੋ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਲਈ ਫੀਲਡ ਸਮੀਕਰਨਾਂ ਮਿਲ ਸਕਣ।
- --- 2
ਫੇਰ, ਇਸ ਲਗਰਾਂਜੀਅਨ ਤੋਂ ਇਹ ਦੋ ਰਕਮਾਂ ਮਿਲਦੀਆਂ ਹਨ,
ਇਹਨਾਂ ਨੂੰ ਵਾਪਿਸ ਇਲੁਰ-ਲਗਰਾਂਜੀਅਨ ਸਮੀਕਰਨ 2 ਵਿੱਚ ਭਰਦੇ ਹੋਏ,
ਕੰਪਲੈਕਸ ਕੰਜੂਗੇਟ ਨਾਲ
ਵਿਚਕਾਰਲੀ ਰਕਮ ਨੂੰ ਸੱਜੇ ਪਾਸੇ ਲਿਆਉਣ ਨਾਲ ਦੂਜੀ ਸਮੀਕਰਨ ਇਸ ਵਿੱਚ ਤਬਦੀਲ ਹੋ ਜਾਂਦੀ ਹੈ,
ਖੱਬਾ ਪਾਸਾ ਮੂਲ ਡੀਰਾਕ ਇਕੁਏਸ਼ਨ ਵਰਗਾ ਹੈ ਅਤੇ ਸੱਜਾ ਪਾਸਾ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਫੀਲਡ ਨਾਲ ਪਰਸਪਰ ਕ੍ਰਿਆ ਹੈ।
ਇਸ ਵਕਤ ਫੀਲਡ ਲਈ, ਉੱਪਰ ਦਰਸਾਏ ਲਗਰਾਂਜੀਅਨ ਨੂੰ ਇੱਕ ਹੋਰ ਇਲੁਰ-ਲਗਰਾਂਜੀਅਨ ਇਕੁਏਸ਼ਨ ਵਿੱਚ ਭਰਕੇ ਇੱਕ ਹੋਰ ਮਹੱਤਵਪੂਰਨ ਇਕੁਏਸ਼ਨ ਖੋਜੀ ਜਾ ਸਕਦੀ ਹੈ:
- ----3
ਇਸ ਵਕਤ ਦੋਵੇਂ ਰਕਮਾਂ ਇਹ ਹੁੰਦੀਆਂ ਹਨ,
ਅਤੇ ਇਹ ਦੋਵੇਂ ਰਕਮਾਂ, ਜਦੋਂ ਵਾਪਿਸ ਸਮੀਕਰਨ 3 ਵਿੱਚ ਭਰੀਆਂ ਜਾਂਦੀਆਂ ਹਨ, ਸਾਨੂੰ ਇਹ ਦਿੰਦੀਆਂ ਹਨ,
ਹੁਣ, ਜੇਕਰ ਅਸੀਂ ਲੌਰੰਜ ਗੇਜ ਕੰਡੀਸ਼ਨ ਥੋਪੀਏ, ਤਾਂ ਫੋਰ ਪੁਟੈਸ਼ਨ ਦਾ ਡਾਇਵੇਰਜੰਸ ਮੁੱਕ ਜਾਂਦਾ ਹੈ,
ਫੇਰ ਸਾਨੂੰ ਇਹ ਮਿਲਦਾ ਹੈ,
ਜੋ ਫੋਰ ਪੁਟੈਂਸ਼ਲ ਲਈ ਵੇਵ ਇਕੁਏਸ਼ਨ ਹੁੰਦੀ ਹੈ, ਜੋ ਲੌਰੰਜ਼ ਗੇਜ ਵਿੱਚ ਕਲਾਸੀਕਲ ਮੈਕਸਵੈੱਲ ਸਮੀਕਰਨਾਂ ਦਾ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਰੂਪ ਹੈ। (ਉੱਪਰ ਦਰਸਾਈ ਸਮੀਕਰਨ ਵਿੱਚ, ਵਰਗ, ਡੀ’ਅਲਬ੍ਰਟ ਓਪਰੇਟਰ ਨੂੰ ਪ੍ਰਸਤੁਤ ਕਰਦਾ ਹੈ)
ਪਰਸਪਰ ਕ੍ਰਿਆ ਤਸਵੀਰ
[ਸੋਧੋ]ਇਹ ਥਿਊਰੀ ਬੋਸੌਨਿਕ ਅਤੇ ਫਰਮੀਔਨਿਕ ਸੈਕਟਰਾਂ ਨੂੰ ਸੁਤੰਤਰ ਸਮਝ ਕੇ ਸਿੱਧੀ ਹੀ ਕੁਆਂਟਾਇਜ਼ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ। ਇਹ ਸਾਨੂੰ ਅਸਿੰਪਟੋਟਿਕ ਅਵਸਥਾਵਾਂ ਦਾ ਇੱਕ ਸੈੱਟ ਰਚਣ ਦੀ ਪ੍ਰਵਾਨਗੀ ਦਿੰਦੀ ਹੈ ਜੋ ਵੱਖਰੀਆਂ ਪ੍ਰਕ੍ਰਿਆਵਾਂ ਲਈ ਖੋਜਯੋਗਤਾ (ਪ੍ਰੋਬੇਬਿਲਟੀ) ਐਂਪਲੀਟਿਊਡਾਂ ਦਾ ਹਿਸਾਬ ਲਗਾਉਣਾ ਸ਼ੁਰੂ ਕਰਨ ਲਈ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਅਜਿਹਾ ਕਰਨ ਲਈ, ਸਾਨੂੰ ਇੱਕ ਐਵੋਲੀਊਸ਼ਨ (ਉਤਪਤੀ) ਓਪਰੇਟਰ ਦਾ ਹਿਸਾਬ ਲਗਾਉਣਾ ਪਵੇਗਾ ਜੋ , ਕਿਸੇ ਦਿੱਤੀ ਹੋਈ ਸ਼ੁਰੂਆਤੀ ਅਵਸਥਾ ਲਈ, ਇੱਕ ਅਜਿਹੇ ਤਰੀਕੇ ਨਾਲ ਅੰਤਿਮ ਅਵਸਥਾ ਦੇਵੇਗਾ ਕਿ ਇਹ ਮਿਲ ਸਕੇ
ਇਸ ਤਕਨੀਕ ਨੂੰ S-ਮੈਟ੍ਰਿਕਸ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਉਤਪਤੀ ਓਪਰੇਟਰ ਪਰਸਪਰ ਕ੍ਰਿਆ ਤਸਵੀਰ ਵਿੱਚੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ਜਿੱਥੇ ਪਰਸਪਰ ਕ੍ਰਿਆ ਹੈਮਿਲਟੋਨੀਅਨ ਦੁਆਰਾ ਵਕਤ ਉਤਪਤੀ ਮਿਲਦੀ ਹੈ, ਜੋ ਉੱਪਰ ਦਰਸਾਈ ਲਗਰਾਂਜੀਅਨ ਘਣਤਾ ਵਿਚਲੀ ਦੂਜੀ ਰਕਮ ਦੀ ਸਪੇਸ ਉੱਪਰ ਇੰਟਗ੍ਰਲ ਹੁੰਦਾ ਹੈ;
ਅਤੇ ਇਸਤਰਾਂ, ਇਹ ਮਿਲਦਾ ਹੈ,
ਜਿੱਥੇ T ਟਾਈਮ ਔਰਡਰਿੰਗ ਓਪਰੇਟਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇਹ ਉਤਪਤੀ ਓਪਰੇਟਰ ਸਿਰਫ ਇੱਕ ਲੜੀ ਵਜੋਂ ਅਰਥ ਰੱਖਦਾ ਹੈ, ਅਤੇ ਜੋ ਸਾਨੂੰ ਇੱਥੇ ਮਿਲਦਾ ਹੈ ਉਹ ਵਿਕਾਸ ਮਾਪਦੰਡ ਦੇ ਤੌਰ ਤੇ ਬਾਰੀਕ ਬਣਤਰ ਸਥਿਰਾਂਕ ਵਾਲਾ ਪਰਚਬੇਸ਼ਨ ਸੀਰੀਜ਼ ਹੈ। ਇਸ ਸੀਰੀਜ਼ ਨੂੰ ਡੇਅਸਨ ਸੀਰੀਜ਼ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।
ਫੇਨਮੈਨ ਚਿੱਤਰ
[ਸੋਧੋ]ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਪ੍ਰਤਿ ਇਸ ਫੇਨਮੈਨ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਦੀ ਸੰਕਲਪਿਕ ਸਪੱਸ਼ਟਤਾ ਦੇ ਬਾਵਜੂਦ, ਲੱਗਭੱਗ ਕਿਸੇ ਵੀ ਸ਼ੁਰੂਆਤੀ ਪੁਸਤਕ ਨੇ ਅਪਣੀ ਪੇਸ਼ਕਸ਼ ਵਿੱਚ ਫੇਨਮੈਨ ਨੂੰ ਨਹੀਂ ਅਪਣਾਇਆ। ਕੈਲਕੁਲੇਸ਼ਨਾਂ ਕਰਦੇ ਵਕਤ ਪ੍ਰਚਾਰਕਾਂ ਦੇ ਫੋਰੀਅਰ ਟਰਾਂਸਫੌਰਮਾਂ ਨਾਲ ਕੰਮ ਕਰਨਾ ਬਹੁਤ ਅਸਾਨ ਹੁੰਦਾ ਹੈ। ਕੁਆਂਟਮ ਫਿਜ਼ਿਕਸ ਕਣਾਂ ਦੀਆਂ ਪੁਜ਼ੀਸ਼ਨਾਂ ਦੀ ਜਗਹ ਉਹਨਾਂ ਦੇ ਮੋਮੈਂਟਾਂ ਨੂੰ ਲੈਂਦੀ ਹੈ, ਅਤੇ ਕਣਾਂ ਬਾਰੇ ਇਹ ਸੋਚਣਾ ਅਸਾਨੀਜਨਕ ਰਹਿੰਦਾ ਹੈ ਕਿ ਉਹ ਬਣਦੇ ਤੇ ਵਿਨਾਸ਼ ਹੁੰਦੇ ਰਹਿੰਦੇ ਹਨ ਜਦੋਂ ਉਹ ਪਰਸਪਰ ਕ੍ਰਿਆ ਕਰਦੇ ਹਨ। ਫੇਨਮੈਨ ਚਿੱਤਰ ਫੇਰ ਉਸੇ ਤਰਾਂ ਨਜ਼ਰ ਆਉਂਦੇ ਹਨ, ਪਰ ਰੇਖਾਵਾਂ ਵੱਖਰੀਆਂ ਵਿਆਖਿਆਵਾਂ ਰੱਖਦੀਆਂ ਹਨ। ਇਲੈਕਟ੍ਰੌਨ ਰੇਖਾ ਦਿੱਤੀ ਹੋਈ ਊਰਜਾ ਅਤੇ ਮੋਮੈਂਟਮ ਵਾਲੇ ਇੱਕ ਇਲੈਕਟ੍ਰੌਨ ਨੂੰ ਪ੍ਰਸਤੁਤ ਕਰਦੀ ਹੈ, ਜੋ ਫੋਟੌਨ ਰੇਖਾ ਦੀ ਵਿਆਖਿਆ ਨਾਲ ਮਿਲਦੀ ਜੁਲਦੀ ਹੈ। ਇੱਕ ਵਰਟੈਕਸ ਚਿੱਤਰ ਇੱਕ ਫੋਟੌਨ ਦੀ ਰਚਨਾ ਜਾਂ ਵਿਨਾਸ਼ ਰਾਹੀਂ ਇੱਕ ਇਲੈਕਟ੍ਰੌਨ ਦਾ ਵਿਨਾਸ਼ ਤੇ ਦੂਜੇ ਦੀ ਰਚਨਾ ਪ੍ਰਸਤੁਤ ਕਰਦਾ ਹੈ, ਜਿਸ ਵਿੱਚ ਹਰੇਕ ਕਣ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ ਊਰਜਾਵਾਂ ਅਤੇ ਮੋਮੈਂਟਾ ਹੁੰਦੇ ਹਨ। ਡੇਅਸਨ ਸੀਰੀਜ਼ ਦੀਆਂ ਰਕਮਾਂ ਉੱਤੇ ਵਿੱਕ ਥਿਊਰਮ ਵਰਤਦੇ ਹੋਏ, ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਲਈ S-ਮੈਟ੍ਰਿਕਸ ਦੀਆਂ ਸਾਰੀਆਂ ਰਕਮਾਂ ਨੂੰ ਫੇਨਮੈਨ ਚਿੱਤਰਾਂ ਦੀ ਤਕਨੀਕ ਰਾਹੀਂ ਗਿਣਿਆ ਮਿਣਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਇਸ ਮਾਮਲੇ ਵਿੱਚ ਡਰਾਇੰਗ ਲਈ ਕਨੂੰਨ ਹੇਠਾਂ ਲਿਖੇ ਹਨ;
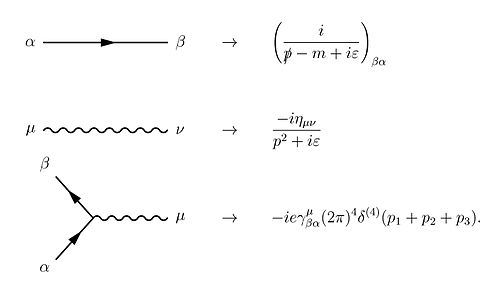

ਇਹਨਾਂ ਕਨੂੰਨਾਂ ਵਿੱਚ ਸਾਨੂੰ ਬੰਦ ਲੂਪਾਂ ਵਾਸਤੇ ਇੱਕ ਹੋਰ ਕਨੂੰਨ ਜੋੜਨਾ ਪਏਗਾ ਜੋ ਮੋਮੈਂਟਾ ਉੱਤੇ ਇੱਕ ਇੰਟੀਗ੍ਰੇਸ਼ਨ ਦਾ ਅਰਥ ਰੱਖਦਾ ਹੈ, ਕਿਉਂਕਿ ਇਹ ਅੰਦਰੂਨੀ (ਵਰਚੁਅਲ) ਕਣ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਊਰਜਾ-ਮੋਮੈਂਟਮ ਤੱਕ ਸੀਮਤ ਨਹੀਂ ਹੁੰਦੇ- ਭਾਵੇਂ ਜੋ ਸਪੈਸ਼ਲ ਰਿਲੇਟੀਵਿਟੀ ਰਾਹੀਂ ਆਮ ਤੌਰ ਤੇ ਜਰੂਰੀ ਹੁੰਦਾ ਹੈ। ਇਹਨਾਂ ਤੋਂ, ਪ੍ਰੋਬੇਬਿਲਟੀ ਐਂਪਲੀਟਿਊਡਾਂ ਦੇ ਹਿਸਾਬ ਕਿਤਾਬ ਸਿੱਧੇ ਹੀ ਮਿਲ ਜਾਂਦੇ ਹਨ। ਇੱਕ ਉਦਾਹਰਨ, ਇਲਾਸਟਿਕ ਸਕੈਟ੍ਰਿੰਗ ਅਧੀਨ ਇੱਕ ਇਲੈਕਟ੍ਰੌਨ ਅਤੇ ਇੱਕ ਫੋਟੌਨ ਵਾਲੀ ਕੌਂਪਟਨ ਸਕੈਟ੍ਰਿੰਗ ਹੈ।

ਅਤੇ ਇਸਤਰਾਂ ਅਸੀਂ S-ਮੈਟ੍ਰਿਕਸ ਲਈ ਇੱਕ ਪਰਚਰਬੇਸ਼ਨ ਸੀਰੀਜ਼ ਦੇ ਪਹਿਲੇ ਦਰਜੇ ਉੱਤੇ ਸਬੰਧਤ ਐਂਪਲੀਟਿਊਡ ਪ੍ਰਾਪਤ ਕਰਨ ਵਿੱਚ ਸਫਲ ਰਹਿੰਦੇ ਹਾਂ:
ਜਿਸਤੋਂ ਅਸੀਂ ਇਸ ਸਕੈਟ੍ਰਿੰਗ ਵਾਸਤੇ ਕ੍ਰੌਸ ਸੈਕਸ਼ਨ (ਕਾਟ ਹਿੱਸਾ) ਪਤਾ ਕਰਨ ਵਿੱਚ ਸਫਲ ਰਹਿੰਦੇ ਹਾਂ।
ਪੁਨਰ-ਮਾਨਕੀਕਰਨ
[ਸੋਧੋ]ਉੱਚ ਕ੍ਰਮ ਰਕਮਾਂ ਨੂੰ ਉਤਪਤੀ ਓਪਰੇਟਰ ਲਈ ਸਿੱਧਾ ਹੀ ਪਤਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਪਰ ਇਹ ਰਕਮਾਂ ਹੇਠਾਂ ਦਰਸਾਏ ਅਜਿਹੇ ਸਰਲ ਚਿੱਤਰ ਦਿਖਾਉਂਦੀਆਂ ਹਨ, ਜੋ ਬੰਦ ਲੂਪ ਹੁੰਦੇ ਹੋਏ, ਗਣਿਤਿਕ ਅਰਥ ਤੋਂ ਬਗੈਰ ਫੈਲ ਰਹੇ ਇੰਟਗ੍ਰਲ ਦੀ ਹਾਜ਼ਰੀ ਦੱਸਦੇ ਹਨ।
-
ਵੈਕੱਮ ਪੋਲਰਾਇਜ਼ੇਸ਼ਨ ਫੰਕਸ਼ਨ ਪ੍ਰਤਿ ਇੱਕ-ਲੂਪ ਯੋਗਦਾਨ
-
ਇਲੈਕਟ੍ਰੌਨ ਸਵੈ-ਊਰਜਾ ਫੰਕਸ਼ਨ ਪ੍ਰਤਿ ਇੱਕ-ਲੂਪ ਯੋਗਦਾਨ
-
ਵਰਟੈਕਸ ਫੰਕਸ਼ਨ ਪ੍ਰਤਿ ਇੱਕ-ਲੂਪ ਯੋਗਦਾਨ
ਇਸ ਕਠਿਨਾਈ ਨਾਲ ਨਿਬਟਣ ਲਈ, ਪੁਨਰ-ਮਾਨਕੀਕਰਨ (ਰੀਨੌਰਮਲਾਇਜ਼ੇਸ਼ਨ) ਨਾਮ ਦੀ ਤਕਨੀਕ ਤਿਆਰ ਕੀਤੀ ਗਈ ਹੈ, ਜਿਸਨੇ ਪ੍ਰਯੋਗਾਂ ਨਾਲ ਬਹੁਤ ਨਜ਼ਦੀਕੀ ਸਹਿਮਤੀ ਵਿੱਚ ਸੀਮਤ ਨਤੀਜੇ ਦਿੱਤੇ ਹਨ। ਇਹ ਨੋਟ ਕਰਨਾ ਮਹੱਤਵਪੂਰਨ ਹੈ ਕਿ ਪੁਨਰ-ਮਾਨਕੀਕਰਨ ਤੋਂ ਬਾਦ ਥਿਊਰੀ ਦੇ ਅਰਥ-ਭਰਪੂਰ ਹੋਣ ਲਈ ਕਸੌਟੀ ਇਹ ਹੁੰਦੀ ਹੈ ਕਿ ਫੈਲ ਰਹੇ ਚਿੱਤਰਾਂ ਦੀ ਸੰਖਿਆ ਸੀਮਤ ਹੋਵੇ। ਇਸ ਮਾਮਲੇ ਵਿੱਚ ਥਿਊਰੀ ਨੂੰ ਪੁਨਰ-ਮਾਨਕੀਕਰਨਯੋਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇਸਦੇ ਪਿੱਛੇ ਦਾ ਕਾਰਣ ਇਹ ਹੈ ਕਿ ਨਿਰੀਖਣਯੋਗਾਂ (ਔਬਜ਼ਰਵੇਬਲਾਂ) ਦੀ ਪੁਨਰ-ਮਾਨਕੀਕਰਨਯੋਗਤਾ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਸੀਮਤ ਸੰਖਿਆ ਦੇ ਸਥਿਰਾਂਕਾਂ ਦੀ ਜਰੂਰਤ ਪੈਂਦੀ ਹੈ ਤਾਂ ਜੋ ਥਿਊਰੀ ਦੇ ਅਨੁਮਾਨਿਤ ਮੁੱਲ ਨੂੰ ਅਣਛੂਹਿਆ ਕਾਇਮ ਰੱਖਿਆ ਜਾਵੇ। ਇਹ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਦਾ ਉਹ ਮਾਮਲਾ ਹੈ ਜਿਸ ਵਿੱਚ ਸਿਰਫ ਤਿੰਨ ਫੈਲ ਰਹੇ ਚਿੱਤਰ (ਡਾਇਵਰਜਿੰਗ ਡਾਇਗ੍ਰਾਮ) ਹੀ ਦਿਖਾਏ ਜਾਂਦੇ ਹਨ। ਇਹ ਵਿਧੀ ਅਜਿਹੇ ਨਿਰੀਖਣਯੋਗ (ਔਬਜ਼ਰਵੇਬਲ) ਦਿੰਦੀ ਹੈ ਜੋ ਪ੍ਰਯੋਗਾਂ ਨਾਲ ਬਹੁਤ ਨਜ਼ਦੀਕੀ ਸਹਿਮਤੀ ਵਿੱਚ ਹੁੰਦੇ ਹਨ ਜਿਵੇਂ ਉਦਾਹਰਨ ਵਜੋਂ ਇਲੈਕਟ੍ਰੌਨ ਜਾਇਰੋਮੈਗਨੈਟਿਕ ਅਨੁਪਾਤ ਵਿੱਚ ਦੇਖਿਆ ਜਾਂਦਾ ਹੈ।
ਪੁਨਰਮਾਨਕੀਕਰਨਯੋਗਤਾ ਕਿਸੇ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਦੇ ਸਫਲਤਾ ਪੂਰਵਕ ਕੰਮ ਕਰਨ ਵਾਲੀ ਥਿਊਰੀ ਦੇ ਤੌਰ ਤੇ ਵਿਚਾਰੇ ਜਾਣ ਲਈ ਇੱਲ ਲਾਜ਼ਮੀ ਕਸੌਟੀ ਬਣ ਗਈ ਹੈ। ਗਰੈਵੀਟੇਸ਼ਨ, ਜਿਸਦਾ ਕੁਆਂਟਮ ਵਿਰੋਧੀਸਾਥੀ ਅਜੱਕਲ ਖੋਜ ਅਧੀਨ ਹੈ, ਨੂੰ ਛੱਡ ਕੇ ਮੁਢਲੀਆਂ ਪਰਸਪਰ ਕ੍ਰਿਆਵਾਂ ਦਰਸਾਉਣ ਵਾਲੀਆਂ ਸਾਰੀਆਂ ਥਿਊਰੀਆਂ ਪੁਨਰ-ਮਾਨਕੀਕਰਨਯੋਗ ਥਿਊਰੀਆਂ ਹੁੰਦੀਆਂ ਹਨ।
ਸੀਰੀਜ਼ ਦੀ ਗੈਰ-ਕਨਵਰਜੰਸ
[ਸੋਧੋ]ਫਰੀਮੈਨ ਡੇਅਸਨ ਦਾ ਇੱਕ ਤਰਕ ਦਿਖਾਉਂਦਾ ਹੈ ਕਿ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਵਿੱਚ ਪਰਚਰਬੇਸ਼ਨ ਸੀਰੀਜ਼ ਦੇ ਕਨਵਰਜੰਸ ਦਾ ਰੇਡੀਅਸ ਜ਼ੀਰੋ ਹੁੰਦਾ ਹੈ। ਮੁਢਲਾ ਤਰਕ ਕੁੱਝ ਇਸਤਰਾਂ ਹੈ: ਜੇਕਰ ਕਪਲਿੰਗ ਸਥਿਰਾਂਕ ਨੈਗਟਿਵ ਹੁੰਦੇ, ਤਾਂ ਇਹ ਕੂਲੌਂਬ ਫੋਰਸ ਸਥਿਰਾਂਕ ਦੇ ਨੈਗੈਟਵ ਹੋਣ ਬਰਾਬਰ ਹੁੰਦਾ। ਇਸਨੇ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਪਰਸਪਰ ਕ੍ਰਿਆ ਉਲਟਾ ਦਿੱਤੀ ਹੁੰਦੀ ਤਾਂ ਜੋ ਇੱਕੋ ਜਿਹੇ ਚਾਰਜ ਖਿੱਚਦੇ ਅਤੇ ਉਲਟੇ ਚਾਰਜ ਧੱਕਦੇ। ਇਸਨੇ ਵੈਕੱਮ ਨੂੰ ਬ੍ਰਹਿਮੰਡ ਦੇ ਇੱਕ ਪਾਸੇ ਇਲੈਕਟ੍ਰੌਨਾਂ ਦੇ ਝੁੰਡ ਨੂੰ ਅਤੇ ਦੂਜੇ ਪਾਸੇ ਪੌਜ਼ੀਟ੍ਰੌਨਾਂ ਦੇ ਝੁੰਡ ਵਿੱਚ ਵਿਕੀਰਣ ਤੋਂ ਉਲਟ ਅਸਥਿਰ ਛੱਡ ਦਿੱਤਾ ਹੁੰਦਾ। ਕਿਉਂਕਿ ਕਪਲਿੰਗ ਸਥਿਰਾਂਕ ਦੇ ਨੈਗਟਿਵ ਮੁੱਲ ਵਾਸਤੇ ਥਿਊਰੀ ਕਮਜੋਰ ਹੈ, ਇਸਲਈ ਸੀਰੀਜ਼ ਇੱਕੋ ਬਿੰਦੂ ਉੱਤੇ ਇਕੱਠੇ ਨਹੀਂ ਹੁੰਦੇ, ਸਗੋਂ ਇੱਕ ਅਸਿੰਪਟੋਟਿਕ ਸੀਰੀਜ਼ ਹੁੰਦੇ ਹਨ।
ਇੱਕ ਅਜੋਕੇ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਤੋਂ, ਅਸੀਂ ਕਹਿੰਦੇ ਹਾਂ ਕਿ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ, ਮਨਚਾਹੀ ਉੱਚ ਊਰਜਾ ਤੱਕ ਕਿਸੇ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਦੇ ਰੂਪ ਵਿੱਚ ਚੰਗੀ ਤਰਾਂ ਪਰਿਭਾਸ਼ਿਤ ਥਿਊਰੀ ਨਹੀਂ ਹੈ। ਸੀਮਤ ਊਰਜਾ ਉੱਤੇ ਮੇਲਣ ਵਾਲੇ (ਕਪਲਿੰਗ) ਸਥਿਰਾਂਕ, ਇੱਕ ਲਾਨਦਾਓ ਪੋਲ ਵੱਲ ਇਸ਼ਾਰਾ ਕਰਦੇ ਹੋਏ, ਅਨੰਤ ਤੱਕ ਭੱਜ ਤੁਰਦੇ ਹਨ। ਲਾਜ਼ਮੀ ਤੌਰ ਤੇ ਸਮੱਸਿਆ ਇਹ ਹੈ ਕਿ ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ, ਕੁਆਂਟਮ ਸੂਖਮਤਾ ਮਸਲਿਆਂ ਤੋਂ ਮੁਸ਼ਕਿਲਾਂ ਨਾਲ ਘਿਰੀ ਦਿਸਦੀ ਹੈ। ਕੁਆਂਟਮ ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਨੂੰ ਕਿਸੇ ਵਿਸ਼ਾਲ ਸੰਯੁਕਤ ਥਿਊਰੀ (ਗ੍ਰੈਂਡ ਯੂਨੀਫਾਈਡ ਥਿਊਰੀ) ਅੰਦਰ ਜੜੇ ਜਾਣ ਲਈ ਪ੍ਰੇਰਣਾਵਾਂ ਵਿੱਚੋਂ ਇਹ ਇੱਕ ਪ੍ਰੇਰਣਾ ਹੈ।
ਇਹ ਵੀ ਦੇਖੋ
[ਸੋਧੋ]ਹਵਾਲੇ
[ਸੋਧੋ]- ↑ Feynman, Richard (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN 978-0-691-12575-6.
- ↑ P.A.M. Dirac (1927). "The Quantum Theory of the Emission and Absorption of Radiation". Proceedings of the Royal Society of London A. 114 (767): 243–265. Bibcode:1927RSPSA.114..243D. doi:10.1098/rspa.1927.0039.
- ↑ E. Fermi (1932). "Quantum Theory of Radiation". Reviews of Modern Physics. 4: 87–132. Bibcode:1932RvMP....4...87F. doi:10.1103/RevModPhys.4.87.
- ↑ 4.0 4.1 V. F. Weisskopf (1939). "On the Self-Energy and the Electromagnetic Field of the Electron". Physical Review. 56: 72–85. Bibcode:1939PhRv...56...72W. doi:10.1103/PhysRev.56.72.
- ↑ R. Oppenheimer (1930). "Note on the Theory of the Interaction of Field and Matter". Physical Review. 35 (5): 461–477. Bibcode:1930PhRv...35..461O. doi:10.1103/PhysRev.35.461.
- ↑ Lamb, Willis; Retherford, Robert (1947). "Fine Structure of the Hydrogen Atom by a Microwave Method,". Physical Review. 72 (3): 241–243. Bibcode:1947PhRv...72..241L. doi:10.1103/PhysRev.72.241.
- ↑ Foley, H.; Kusch, P. (1948). "On the Intrinsic Moment of the Electron". Physical Review. 73 (3): 412. Bibcode:1948PhRv...73..412F. doi:10.1103/PhysRev.73.412.
- ↑ Schweber, Silvan (1994). "Chapter 5". QED and the Men Who Did it: Dyson, Feynman, Schwinger, and Tomonaga. Princeton University Press. p. 230. ISBN 978-0-691-03327-3.
- ↑ H. Bethe (1947). "The Electromagnetic Shift of Energy Levels". Physical Review. 72 (4): 339–341. Bibcode:1947PhRv...72..339B. doi:10.1103/PhysRev.72.339.
- ↑ S. Tomonaga (1946). "On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields". Progress of Theoretical Physics. 1 (2): 27–42. doi:10.1143/PTP.1.27.
- ↑ J. Schwinger (1948). "On Quantum-Electrodynamics and the Magnetic Moment of the Electron". Physical Review. 73 (4): 416–417. Bibcode:1948PhRv...73..416S. doi:10.1103/PhysRev.73.416.
- ↑ J. Schwinger (1948). "Quantum Electrodynamics. I. A Covariant Formulation". Physical Review. 74 (10): 1439–1461. Bibcode:1948PhRv...74.1439S. doi:10.1103/PhysRev.74.1439.
- ↑ R. P. Feynman (1949). "Space–Time Approach to Quantum Electrodynamics". Physical Review. 76 (6): 769–789. Bibcode:1949PhRv...76..769F. doi:10.1103/PhysRev.76.769.
- ↑ R. P. Feynman (1949). "The Theory of Positrons". Physical Review. 76 (6): 749–759. Bibcode:1949PhRv...76..749F. doi:10.1103/PhysRev.76.749.
- ↑ R. P. Feynman (1950). "Mathematical Formulation of the Quantum Theory of Electromagnetic Interaction". Physical Review. 80 (3): 440–457. Bibcode:1950PhRv...80..440F. doi:10.1103/PhysRev.80.440.
- ↑ F. Dyson (1949). "The Radiation Theories of Tomonaga, Schwinger, and Feynman". Physical Review. 75 (3): 486–502. Bibcode:1949PhRv...75..486D. doi:10.1103/PhysRev.75.486.
- ↑ F. Dyson (1949). "The S Matrix in Quantum Electrodynamics". Physical Review. 75 (11): 1736–1755. Bibcode:1949PhRv...75.1736D. doi:10.1103/PhysRev.75.1736.
ਹੋਰ ਲਿਖਤਾਂ
[ਸੋਧੋ]ਪੁਸਤਕਾਂ
[ਸੋਧੋ]- De Broglie, Louis (1925). Recherches sur la theorie des quanta [Research on quantum theory]. France: Wiley-Interscience.
- Feynman, Richard Phillips (1998). Quantum Electrodynamics (New ed.). Westview Press. ISBN 978-0-201-36075-2.
- Jauch, J.M.; Rohrlich, F. (1980). The Theory of Photons and Electrons. Springer-Verlag. ISBN 978-0-387-07295-1.
- Greiner, Walter; Bromley, D.A.; Müller, Berndt (2000). Gauge Theory of Weak Interactions. Springer. ISBN 978-3-540-67672-0.
- Kane, Gordon, L. (1993). Modern Elementary Particle Physics. Westview Press. ISBN 978-0-201-62460-1.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Miller, Arthur I. (1995). Early Quantum Electrodynamics: A Sourcebook. Cambridge University Press. ISBN 978-0-521-56891-3.
- Milonni, Peter W., (1994) The quantum vacuum - an introduction to quantum electrodynamics. Academic Press. ISBN 0-12-498080-5
- Schweber, Silvan S. (1994). QED and the Men Who Made It. Princeton University Press. ISBN 978-0-691-03327-3.
- Schwinger, Julian (1958). Selected Papers on Quantum Electrodynamics. Dover Publications. ISBN 978-0-486-60444-2.
- Tannoudji-Cohen, Claude; Dupont-Roc, Jacques; Grynberg, Gilbert (1997). Photons and Atoms: Introduction to Quantum Electrodynamics. Wiley-Interscience. ISBN 978-0-471-18433-1.
ਰਸਾਲੇ
[ਸੋਧੋ]- Dudley, J.M.; Kwan, A.M. (1996). "Richard Feynman's popular lectures on quantum electrodynamics: The 1979 Robb Lectures at Auckland University". American Journal of Physics. 64 (6): 694–698. Bibcode:1996AmJPh..64..694D. doi:10.1119/1.18234.































![{\displaystyle U=T\exp \left[-{\frac {i}{\hbar }}\int _{t_{0}}^{t}dt'V(t')\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6e8e9f54c6af1da0a81554513dab4bb8ba02f18)






