ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼
| ਇਹ ਲੇਖ ਅਧਾਰ ਹੈ। ਤੁਸੀਂ ਇਸਨੂੰ ਵਧਾਕੇ ਵਿਕੀਪੀਡੀਆ ਦੀ ਮੱਦਦ ਕਰ ਸਕਦੇ ਹੋ। |
ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ (ਜਿਸਨੂੰ ਸੁਪਰਲਿਊਮੀਨਲ ਜਾਂ FTL ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ) ਸੰਚਾਰ (ਕਮਿਉਨੀਕੇਸ਼ਨ) ਅਤੇ ਯਾਤਰਾ ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਤੋਂ ਵੀ ਤੇਜ਼ ਸਪੀਡ ਨਾਲ ਪਦਾਰਥ ਜਾਂ ਸੂਚਨਾ ਦੇ ਸੰਚਾਰ ਵੱਲ ਇਸ਼ਾਰਾ ਕਰਦੀ ਹੈ। ਸਪੈਸ਼ਲ ਰਿਲੇਟੀਵਿਟੀ ਦੀ ਥਿਊਰੀ ਅਧੀਨ, ਸਬਲਿਊਮੀਨਲ ਵਿਲੌਸਿਟੀ ਵਾਲਾ ਕੋਈ ਕਣ (ਜਿਸਦਾ ਰੈਸਟ ਪੁੰਜ ਹੋਵੇ) ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਤੱਕ ਪ੍ਰਵੇਗਿਤ (ਐਕਸਲਰੇਟ) ਕਰਨ ਵਾਸਤੇ ਅਨੰਤ ਊਰਜਾ ਦੀ ਮੰਗ ਕਰਦਾ ਹੈ, ਬੇਸ਼ੱਕ ਸਪੈਸ਼ਲ ਰਿਲੇਟੀਵਿਟੀ ਅਜਿਹੇ ਕਣਾਂ ਦੀ ਮੌਜੂਦਗੀ ਤੇ ਕੋਈ ਪਾਬੰਧੀ ਨਹੀਂ ਲਗਾਉ਼ਦੀ ਜੋ ਸਾਰੇ ਵਕਤਾਂ ਉੱਤੇ (ਟੈਕਿਔਨ) ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਸਫ਼ਰ ਕਰਦੇ ਹਨ।
ਦੂਜੇ ਪਾਸੇ, ਜਿਸ ਵੱਲ ਕੁੱਝ ਭੌਤਿਕ ਵਿਗਿਆਨੀ ਸਪੱਸ਼ਟ ਜਾਂ ਪ੍ਰਭਾਵੀ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਹੋਣ ਦਾ ਇਸ਼ਾਰਾ ਕਰਦੇ ਹਨ, ਉਹ ਇਸ ਪਰਿਕਲਪਨਾ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ਕਿ ਸਪੇਸਟਾਈਮ ਦੇ ਖਾਸ ਤੌਰ 'ਤੇ ਵੋਗੜੇ ਹੋਏ ਖੇਤਰ ਪਦਾਰਥ ਨੂੰ ਨਾ ਵਿਗੜੇ ਹੋਏ ਸਪੇਸਟਾਈਮ ਜਾਂ ਸਧਾਰਨ ਸਪੇਸਟਾਈਮ ਅੰਦਰ ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਵਾਲੇ ਵਕਤ ਨਾਲ਼ੋਂ ਘੱਟ ਵਕਤ ਵਿੱਚ ਦੂਰ ਸਥਿਤ ਸਥਾਨਾਂ ਉੱਤੇ ਪਹੁੰਚਣ ਦੀ ਆਗਿਆ ਦੇ ਸਕਦੇ ਹੋਣਗੇ। ਬੇਸ਼ੱਕ ਅਜੋਕੀਆਂ ਥਿਊਰੀਆਂ ਮੁਤਾਬਿਕ ਦੁਆਰਾ ਸਥਾਨਿਕ ਤੌਰ 'ਤੇ ਵਿਗੜੇ ਹੋਏ ਸਪੇਸਟਾਈਮ ਖੇਤਰ ਦੇ ਤੁਲਨਾਤਮਿਕ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਸਪੀਡ ਨਾਲ ਸਫ਼ਰ ਕਰਨ ਵਾਸਤੇ ਅਜੇ ਵੀ ਪਦਾਰਥ ਦੀ ਜਰੂਰਤ ਪੈਂਦੀ ਹੈ, ਜਨਰਲ ਰਿਲੇਟੀਵਿਟੀ ਦੁਆਰਾ ਸਪੱਸ਼ਟ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਸਪੀਡ ਬਾਹਰ ਨਹੀਂ ਕੱਢੀ ਜਾਂਦੀ। ਸਪੱਸ਼ਟ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਪ੍ਰਸਤਾਵਾਂ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਵਿੱਚ ਅਲਕੁਬਿੱਰੇ ਡਰਾਈਵ ਅਤੇ ਟ੍ਰਾਵਰਸੇਬਲ ਵਰਮਹੋਲ ਸ਼ਾਮਿਲ ਹਨ, ਭਾਵੇਂ ਇਹਨਾਂ ਦੀ ਭੌਤਿਕੀ ਮੁਮਕਿਨਤਾ ਅਨਿਸ਼ਚਿਤ ਹੈ।
ਗੈਰ-ਸੂਚਨਾ ਦੀ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਯਾਤਰਾ
[ਸੋਧੋ]ਇਸ ਲੇਖ ਦੇ ਸੰਦਰਭ ਵਿੱਚ, ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਸੂਚਨਾ ਜਾਂ ਪਦਾਰਥ ਦਾ c ਤੋਂ ਤੇਜ਼ ਸੰਚਾਰ ਹੈ, ਜੋ ਕਿਸੇ ਵੈਕੱਮ ਅੰਦਰ ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਸਮਾਨ ਇੱਕ ਸਥਿਰਾਂਕ ਹੈ, ਜਿਸਦਾ ਮੁੱਲ 299,792,458 m/s (ਪਰਿਭਾਸ਼ਾ ਤੋਂ) ਜਾਂ ਤਕਰੀਬਨ 186,282.4 ਮੀਲ ਪ੍ਰਤਿ ਸਕਿੰਟ ਹੁੰਦਾ ਹੈ। ਇਹ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਯਾਤਰਾ ਵਾਂਗ ਨਹੀਂ ਹੈ, ਕਿਉਂਕਿ:
- c ਤੋਂ ਤੇਜ਼ ਕੁੱਝ ਪ੍ਰਕ੍ਰਿਆਵਾਂ ਸੰਚਾਰਿਤ ਹੁੰਦੀਆਂ ਹਨ, ਪਰ ਸੂਚਨਾ ਨਹੀਂ ਲਿਜਾ ਸਕਦੀਆਂ (ਨਾਲ ਵਾਲੇ ਅਗਲੇ ਸੈਕਸ਼ਨ ਵਿੱਚ ਉਦਾਹਰਨਾਂ ਦੇਖੋ)
- ਪ੍ਰਕਾਸ਼ ਉਦੋਂ c/n ਸਪੀਡ ਨਾਲ ਯਾਤਰਾ ਕਰਦਾ ਹੈ ਜਦੋਂ ਕਿਸੇ ਵੈਕੱਮ ਵਿੱਚ ਨਹੀਂ ਹੁੰਦਾ, ਸਗੋਂ ਰਿੱਫਰੈਕਟਿਵ ਸੂਚਕਾਂਕ = n (ਰਿੱਫ੍ਰੈਕਸ਼ਨ ਲਈ ਜਿਮੇਵਾਰ) ਵਾਲੇ ਕਿਸੇ ਮਾਧਿਅਮ ਵਿੱਚੋਂ ਗੁਜ਼ਰ ਰਿਹਾ ਹੁੰਦਾ ਹੈ, ਅਤੇ ਕੁੱਝ ਪਦਾਰਥਾਂ ਵਿੱਚੋਂ ਹੋਰ ਕਣ c/n ਤੋਂ ਤੇਜ਼ ਗਤੀ ਕਰ ਸਕਦੇ ਹਨ, ਜੋ ਚੇਰੇਂਕੋਵ ਰੇਡੀਏਸ਼ਨ ਵੱਲ ਲਿਜਾਂਦਾ ਹੈ। (ਥੱਲੇ ਫੇਜ਼ ਵਿਲੌਸਿਟੀ ਦੇਖੋ)
ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਵੀ ਘਟਨਾਕ੍ਰਮ ਸਪੈਸ਼ਲ ਰਿਲੇਟੀਵਿਟੀ ਦੀ ਉਲੰਘਣਾ ਨਹੀਂ ਕਰਦਾ ਜਾਂ ਕਾਰਣਾਤਮਿਕਤਾ ਨਾਲ ਸਮੱਸਿਆ ਪੈਦਾ ਨਹੀਂ ਕਰਦਾ, ਅਤੇ ਇਸਤਰਾਂ ਨਾ ਹੀ ਇੱਥੇ ਦਰਸਾਇਆ ਕੁੱਝ ਵੀ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਗਤੀ ਵਾਸਤੇ ਨਿਯਮਾਂ ਉੱਤੇ ਪੂਰਾ ਨਹੀਂ ਉਤਰਦਾ।
ਅੱਗੇ ਦਿੱਤੀਆਂ ਉਦਾਹਰਨਾਂ ਵਿੱਚ, ਕੁੱਝ ਪ੍ਰਭਾਵ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਗਤੀ ਕਰਦੇ ਦਿਸ ਸਕਦੇ ਹਨ, ਪਰ ਉਹਨਾਂ ਊਰਜਾ ਜਾਂ ਸੂਚਨਾ ਨੂੰ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਨਹੀਂ ਲਿਜਾਉਂਦੇ, ਇਸਲਈ ਉਹ ਸਪੈਸ਼ਲ ਰਿਲੇਟੀਵਿਟੀ ਦੀ ਉਲੰਘਣਾ ਨਹੀਂ ਕਰਦੇ।
ਅਕਾਸ਼ ਦੀ ਰੋਜ਼ਾਨਾ ਗਤੀ
[ਸੋਧੋ]ਧਰਤੀ ਨਾਲ ਬੰਨੇ (ਜੁੜੇ) ਹੋਏ ਕਿਸੇ ਔਬਜ਼ਰਵਰ (ਨਿਰੀਖਕ) ਲਈ, ਅਕਾਸ਼ ਵਿੱਚ ਚੀਜ਼ਾਂ ਧਰਤੀ ਦੁਆਲੇ 1 ਦਿਨ ਵਿੱਚ ਇੱਕ ਚੱਕਰ ਪੂਰਾ ਕਰਦੀਆਂ ਹਨ। ਸੂਰਜੀ ਸਿਸਟਮ ਤੋਂ ਬਾਹਰ ਦਾ ਸਭ ਤੋਂ ਨਜ਼ਦੀਕੀ ਤਾਰਾ, ਪ੍ਰੌਗਜ਼ਿਮਾ ਸੈਂਚੁਰੀ, ਤਕਰੀਬਨ 4 ਪ੍ਰਕਾਸ਼-ਸਾਮ ਦੂਰ ਹੈ। ਕਿਸੇ ਜੀਓਸਟੇਸ਼ਨਰੀ (ਭੂ-ਸਥਿਰ) ਨਜ਼ਰੀਏ ਨਾਲ, ਪ੍ਰੌਗਜ਼ਿਮਾ ਸੇਂਚੁਰੀ ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ c ਤੋਂ ਕਈ ਗੁਣਾ ਜਿਆਦਾ ਸਪੀਡ ਰੱਖਦਾ ਹੈ ਕਿਉਂਕਿ ਕਿਸੇ ਚੱਕਰ ਵਿੱਚ ਗਤੀਸ਼ੀਲ ਕਿਸੇ ਵਸਤੂ ਦੀ ਰਿਮ (ਕਿਨਾਰਿਆਂ ਵਾਲੀ) ਸਪੀਡ ਰੇਡੀਅਸ ਅਤੇ ਐਂਗੁਲਰ ਸਪੀਡ ਦਾ ਗੁਣਨਫਲ ਹੁੰਦੀ ਹੈ। ਕਿਸੇ ਭੂਸਥਿਰ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਤੋਂ ਇਹ ਵੀ ਸੰਭਵ ਹੈ ਕਿ ਧੁਮਕੇਤੂਆਂ ਵਰਗੀਆਂ ਚੀਜ਼ਾਂ ਅਪਣੀ ਸਪੀਡ ਨੂੰ ਸਬਲਿਊਮੀਨਲ (ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਤੋਂ ਘੱਟ) ਤੋਂ ਸੁਪਰਲਿਊਮੀਨਲ (ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਤੋਂ ਤੇਜ਼) ਸਪੀਡ ਤੱਕ ਤਬਦੀਲ ਕਰਦੀਆਂ ਹੋਣ ਅਤੇ ਸੁਪਰਲਿਊਮੀਨਲ ਤੋਂ ਸਬਲਿਊਮੀਨਲ ਸਪੀਡ ਤੱਕ ਤਬਦੀਲ ਕਰਦੀਆਂ ਹੋਣ ਕਿਉਂਕਿ ਧਰਤੀਂ ਤੋਂ ਦੂਰੀ ਤਬਦੀਲ ਹੁੰਦੀ ਰਹਿੰਦੀ ਹੈ। ਧੁਮਕੇਤੂ ਅਜਿਹੇ ਚੱਕਰਪਥ ਰੱਖਦੇ ਹੋ ਸਕਦੇ ਹਨ ਜੋ ਉਹਨਾਂ ਨੂੰ 1000 AU ਤੋਂ ਵੀ ਜਿਆਦਾ ਬਾਹਰ ਲਿਜਾਂਦੇ ਹੋਣ। 1000 AU ਜਿੰਨੇ ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਕਿਸੇ ਚੱਕਰ ਦਾ ਘੇਰਾ (ਸਰਕਿਉਮਫ੍ਰੈਂਸ) ਇੱਕ ਪ੍ਰਕਾਸ਼ ਦਿਨ ਤੋਂ ਜਿਆਦਾ ਹੁੰਦਾ ਹੈ। ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਕਿਸੇ ਭੂਸਥਿਰ (ਜੀਓਸਟੈਟਿਕ) ਅੰਦਰ ਇੰਨੀ ਅਜਿਹੀ ਦੂਰੀ ਉੱਤੇ ਸਥਿਤ ਧੁਮਕੇਤੂ ਸੁੱਪਰਲਿਊਮੀਨਲ (ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼) ਹੁੰਦੇ ਹਨ, ਅਤੇ ਇਸਲਈ ਗੈਰ-ਇਨਰਸ਼ੀਅਲ (ਗੈਰ-ਜੜਤਾ ਵਾਲੀ) ਫ੍ਰੇਮ (ਢਾਂਚੇ) ਹੁੰਦੇ ਹਨ।
ਪ੍ਰਕਾਸ਼ ਦੇ ਧੱਬੇ ਅਤੇ ਪਰਛਾਵੇਂ
[ਸੋਧੋ]ਜੇਕਰ ਇੱਕ ਲੇਜ਼ਰ ਨੂੰ ਕਿਸੇ ਦੂਰ ਸਥਿਤ ਵਸਤੂ ਦੇ ਆਰਪਾਰ ਲੰਘਾਇਆ ਜਾਵੇ, ਤਾਂ ਲੇਜ਼ਰ ਦਾ ਧੱਬਾ ਅਸਾਨੀ ਨਾਲ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਸਪੀਡ ਉੱਤੇ ਲੰਘਣ ਲਈ ਮਹਬੂਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਇਸੇਤਰਾਂ, ਕਿਸੇ ਦੂਰ ਸਥਿਤ ਵਸਤੂ ਉੱਤੇ ਪਾਇਆ ਗਿਆ ਕੋਈ ਪਰਛਾਵਾਂ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਸਪੀਡ ਨਾਲ ਗਤੀਸ਼ੀਲ ਹੋਣ ਲਈ ਮਜਬੂਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਕਿਸੇ ਵੀ ਮਾਮਲੇ ਵਿੱਚ ਨਾ ਹੀ ਪ੍ਰਕਾਸ਼ ਸੋਮੇ ਤੋਂ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਯਾਤਰਾ ਕਰਦਾ ਹੈ ਅਤੇ ਨਾ ਹੀ ਕੋਈ ਸੂਚਨਾ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਸੰਚਾਰਿਤ ਹੁੰਦੀ ਹੈ।
ਸਥਿਰ ਫੀਲਡ ਪ੍ਰਭਾਵਾਂ ਦਾ ਸਪੱਸ਼ਟ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਸੰਚਾਰ
[ਸੋਧੋ]ਕਿਉਂਕਿ ਸਥਿਰ ਵੇਗ ਨਾਲ ਗਤੀਸ਼ੀਲ ਸੋਮੇ ਵੇਲੇ ਗਰੈਵੀਟੇਸ਼ਨਲ ਜਾਂ ਇਲੈਕਟ੍ਰਿਕ ਸਟੈਟਿਕ ਫੀਲਡ ਦੇ ਸੋਮੇ ਦੀ ਸਪੱਸ਼ਟ ਪੁਜੀਸ਼ਨ ਦੀ ਰਿਟਾਰਡੇਸ਼ਨ (ਰੁਕਾਵਟ) (ਜਾਂ ਅਬੈਰਸ਼ਨ, ਪਤਨ) ਨਹੀਂ ਹੁੰਦੀ, ਇਸਲਈ ਸਥਿਰ ਫੀਲਡ ਪ੍ਰਭਾਵ ਪਹਿਲੀ ਨਜ਼ਰ ਵਿੱਚ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਸਪੀਡ ਨਾਲ ਸੰਚਾਰਿਤ ਹੋਇਆ ਲੱਗ ਸਕਦਾ ਹੈ। ਫੇਰ ਵੀ, ਸਥਿਰ ਸੋਮੇ ਦੀ ਇੱਕਸਾਰ ਗਤੀ ਨੂੰ ਰੈੱਫਰੈਂਸ ਫ੍ਰੇਮ ਅੰਦਰ ਇੱਕ ਤਬਦੀਲੀ ਕਰਕੇ ਹਟਾਇਆ ਜਾ ਸਕਦਾ ਹੈ, ਜੋ ਸਥਿਰ ਫੀਲਡ ਦੀ ਦਿਸ਼ਾ ਨੂੰ ਸਾਰੀਆਂ ਹੀ ਦੂਰੀਆਂ ਉੱਤੇ ਤੁਰੰਤ ਬਦਲਣ ਲਈ ਮਜਬੂਰ ਕਰ ਦਿੰਦੀ ਹੈ। ਇਹ ਕੋਈ ਪੁਜੀਸ਼ਨ ਦੀ ਤਬਦੀਲੀ ਨਹੀਂ ਹੁੰਦੀ ਜੋ ਸੰਚਾਰਿਤ ਹੁੰਦੀ ਹੈ, ਅਤੇ ਇਸੇ ਕਾਰਨ ਇਹ ਤਬਦੀਲੀ ਸਪਮੇ ਤੋਂ ਸੂਚਨਾ ਸੰਚਾਰ ਵਾਸਤੇ ਨਹੀਂ ਵਰਤੀ ਜਾ ਸਕਦੀ। ਕੋਈ ਵੀ ਸੂਚਨਾ ਜਾਂ ਪਦਾਰਥ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਸੰਚਾਰਿਤ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ ਜਾਂ ਸੋਮੇ ਤੋਂ ਰਿਸੀਵਰ/ਨਿਰੀਖਕ ਤੱਕ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਫੀਲਡ ਦੁਆਰਾ ਸੰਚਾਰਿਤ ਨਹੀਂ ਹੋ ਸਕਦਾ।
ਨੇੜੇ ਹੁੰਦੀਆਂ ਗਤੀਆਂ
[ਸੋਧੋ]
ਕਿਸੇ ਇਕਲੌਤੀ ਰੈਫਰੈਂਸ ਫ੍ਰੇਮ ਅੰਦਰ ਗਤੀਸ਼ੀਲ ਦੋ ਵਸਤੂਆਂ ਜਿਸ ਦਰ ਨਾਲ ਇੱਕ ਦੂਜੀ ਦੇ ਨੇੜੇ ਆਉਂਦੀਆਂ ਹਨ ਉਸਨੂੰ ਪਰਸਪਰ ਜਾਂ ਨੇੜੇ ਹੁੰਦੀ ਸਪੀਡ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇਹ ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਤੋਂ ਦੁੱਗਣੀ ਤੱਕ ਪਹੁੰਚ ਸਕਦੀ ਹੋਵੇਗੀ, ਜਿਵੇਂ ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਉੱਤੇ ਰੈਫਰੈਂਸ ਫ੍ਰੇਮ ਪ੍ਰਤਿ ਪਰਸਪਰ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਗਤੀਸ਼ੀਲ ਦੋ ਕਣਾਂ ਦੇ ਮਾਮਲੇ ਵਿੱਚ ਹੁੰਦਾ ਹੈ।
ਟਕਰਾਉਣ ਵਾਲੀ ਕਿਸਮ ਦੇ ਪਾਰਟੀਕਲ ਐਕਸਲਰੇਟਰ ਦੀਆਂ ਆਹਮੋ-ਸਾਹਮਣੀਆਂ ਦਿਸ਼ਾਵਾਂ ਤੋਂ ਇੱਕ ਦੂਜੇ ਦੇ ਨੇੜੇ ਆਉਂਦੇ ਤੇਜ਼ ਗਤੀਸ਼ੀਲ ਦੋ ਕਣਾਂ ਦੀ ਕਲਪਨਾ ਕਰੋ। ਨੇੜੇ ਹੁੰਦੀ ਸਪੀਡ ਉਹ ਦਰ ਹੋਵੇਗੀ ਜਿਸ ਉੱਤੇ ਦੋਵੇਂ ਕਣਾਂ ਦਰਮਿਆਨ ਦੂਰੀ ਘਟ ਰਹੀ ਹੁੰਦੀ ਹੈ। ਐਕਸਲਰੇਟਰ ਦੇ ਸਾਪੇਖਿਕ ਅਰਾਮ ਨਾਲ ਖੜੇ ਕਿਸੇ ਦਰਸ਼ਕ (ਔਬਜ਼ਰਵਰ) ਦੇ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਤੋਂ, ਇਹ ਦਰ ਪ੍ਰਕਾਸ਼ ਦੀ ਗਤੀ ਦੇ ਦੁੱਗਣੇ ਤੋਂ ਕੁੱਝ ਘੱਟ ਹੋਵੇਗੀ।
ਸਪੈਸ਼ਲ ਰਿਲੇਟੀਵਿਟੀ ਇਸ ਤੇ ਕੋਈ ਪਾਬੰਧੀ ਨਹੀਂ ਲਗਾਉਂਦੀ। ਇਹ ਸਾਨੂੰ ਦੱਸਦੀ ਹੈ ਕਿ ਕਣਾਂ ਵਿੱਚੋਂ ਕਿਸੇ ਇੱਕ ਕਣ ਦੀ ਵਿਲੌਸਿਟੀ ਨਾਪਣ ਵਾਸਤੇ ਜਨਰਲ ਰਿਲੇਟੀਵਿਟੀ ਵਰਤਣੀ ਗਲਤ ਗੱਲ ਹੈ, ਜਿਵੇਂ ਦੂਜੇ ਕਣ ਦੀ ਦਿਸ਼ਾ ਦੇ ਨਾਲ ਯਾਤਰਾ ਕਰ ਰਹੇ ਕਿਸੇ ਔਬਜ਼ਰਵਰ ਦੁਆਰਾ ਵਿਲੌਸਿਟੀ ਨਾਪਣੀ। ਯਾਨਿ ਕਿ, ਸਪੈਸ਼ਲ ਰਿਲੇਟੀਵਿਟੀ ਅਜਿਹੀਆਂ ਸਾਪੇਖਿਕ ਵਿਲੌਸਿਟੀਆਂ ਨਾਪਣ ਲਈ ਸਹੀ ਫਾਰਮੂਲਾ ਦਿੰਦੀ ਹੈ।
ਪ੍ਰਵੇਗਿਤ ਢਾਂਚੇ ਅੰਦਰ v ਅਤੇ –v ਗਤੀ ਕਰ ਰਹੇ ਕਣਾਂ ਦੀ ਸਾਪੇਖਿਕ ਵਿਲੌਸਿਟੀ ਨੂੰ ਨਾਪਣਾ ਅਨੁਦੇਸ਼ਾਤਮਿਕ ਹੈ, ਜੋ 2v > c ਨੇੜੇ ਹੋ ਰਹੀ ਸਪੀਡ ਨਾਲ ਸਬੰਧਤ ਹੈ। ਸਪੀਡਾਂ ਨੂੰ c, β = v/c ਦੀਆਂ ਯੂਨਿਟਾਂ (ਇਕਾਈਆਂ) ਵਿੱਚ ਲਿਖਦੇ ਹੋਏ:
ਸਹੀ ਗਤੀਆਂ
[ਸੋਧੋ]ਜੇਕਰ ਕੋਈ ਸਪੇਸ-ਸ਼ਿਪ ਕਿਸੇ ਗ੍ਰਹਿ ਤੱਕ ਧਰਤੀ ਤੋਂ ਦੂਰ ਉੱਚ-ਸਪੀਡ ਨਾਲ ਇੱਕ ਪ੍ਰਕਾਸ਼-ਸਾਲ (ਜਿਵੇਂ ਧਰਤੀ ਦੀ ਰੈਸਟ ਫ੍ਰੇਮ ਵਿੱਚ ਨਾਪਿਆ ਜਾਵੇ) ਵਿੱਚ ਯਾਤਰਾ ਕਰਦਾ ਹੈ, ਤਾਂ ਗ੍ਰਹਿ ਤੱਕ ਪਹੁੰਚਣ ਲਈ ਲੱਗਿਆ ਸਮਾਂ ਯਾਤਰੀ ਦੀ ਘੜੀ ਦੁਆਰਾ ਨਾਪਿਆ ਜਾਣ ਤੇ ਇੱਕ ਸਾਲ ਤੋਂ ਘੱਟ ਸਮਾਂ ਹੋ ਸਕਦਾ ਹੈ (ਭਾਵੇਂ ਇਹ ਧਰਤੀ ਉੱਤੇ ਕਿਸੇ ਘੜੀ ਦੁਆਰਾ ਨਾਪਣ ਤੇ ਹਮੇਸ਼ਾਂ ਹੀ ਇੱਕ ਸਾਲ ਤੋਂ ਵੱਧ ਸਮਾਂ ਰਹੇਗਾ)। ਧਰਤੀ ਵਾਲੀ ਫਰੇਮ ਵਿੱਚ ਨਾਪੀ ਗਈ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਨੂੰ ਯਾਤਰੀ ਦੀ ਘੜੀ ਦੁਆਰਾ ਨਾਪੇ ਗਏ ਲੱਗੇ ਸਮੇਂ ਨਾਲ ਵੰਡ (ਤਕਸੀਮ ਕਰ) ਕੇ ਪ੍ਰਾਪਤ ਮੁੱਲ ਨੂੰ ਇੱਕ ਪ੍ਰੌਪਰ (ਸਹੀ) ਸਪੀਡ ਜਾਂ ਇੱਕ ਪ੍ਰੌਪਰ ਵਿਲੌਸਿਟੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਕਿਸੇ ਸਹੀ ਸਪੀਡ ਦੇ ਮੁੱਲ ਉੱਤੇ ਕੋਈ ਸੀਮਾ ਨਹੀਂ ਹੁੰਦੀ ਕਿਉਂਕਿ ਕੋਈ ਸਹੀ ਸਪੀਡ ਕਿਸੇ ਇਕਲੌਤੀ ਇਨਰਸ਼ੀਅਲ ਫਰੇਮ ਅੰਦਰ ਨਾਪੀ ਗਈ ਕਿਸੇ ਸਪੀਡ ਨੂੰ ਪ੍ਰਸਤੁਤ ਨਹੀਂ ਕਰਦੀ। ਇੱਕੋ ਵਕਤ ਉੱਤੇ ਧਰਤੀ ਤੋਂ ਛੱਡਿਆ ਜਾਣ ਵਾਲਾ ਇੱਕ ਪ੍ਰਕਾਸ਼ ਇਸ਼ਾਰਾ (ਲਾਈਟ ਸਿਗਨਲ) ਯਾਤਰੀ ਤੋਂ ਪਹਿਲਾਂ ਨਿਸ਼ਾਨੇ ਉੱਤੇ ਪਹੁੰਚੇਗਾ।
ਧਰਤੀ ਤੋਂ ਕੋਈ ਕਿੰਨੀ ਦੂਰ ਜਾ ਸਕਦਾ ਹੈ?
[ਸੋਧੋ]ਕਿਉਂਕਿ ਕੋਈ ਵੀ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਯਾਤਰਾ ਨਹੀਂ ਕਰ ਸਕਦਾ, ਇਸਲਈ ਇਹ ਨਤੀਜਾ ਕੱਢਿਆ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਜੇਕਰ ਇੱਕ ਇਨਸਾਨ 20 ਅਤੇ 60 ਸਾਲ ਦਰਮਿਆਨ ਵਿਅਸਤ ਰਹੇ ਤਾਂ ਉਹ ਧਰਤੀ ਤੋਂ 40 ਪ੍ਰਕਾਸ਼-ਸਾਲ ਦੂਰ ਤੱਕ ਯਾਤਰਾ ਕਰ ਸਕਦਾ ਹੈ। ਕੋਈ ਯਾਤਰੀ ਕਦੇ ਵੀ ਕੁੱਝ ਉਹਨਾਂ ਤਾਰਾ ਮੰਡਲ਼ਾਂ ਤੋਂ ਜਿਆਦਾ ਦੂਰ ਤੱਕ ਨਹੀਂ ਪਹੁੰਚ ਸਕੇਗਾ ਜੋ ਧਰਤੀ ਤੋਂ 20-40 ਪ੍ਰਕਾਸ਼-ਸਾਲਾਂ ਦੀ ਸੀਮਾ ਅੰਦਰ ਮੌਜੂਦ ਹੁੰਦੇ ਹਨ। ਇਹ ਇੱਕ ਗਲਤ ਸਮਝੀ ਗਈ ਗੱਲ ਹੈ: ਟਾਈਮ ਡਿਲੇਸ਼ਨ ਕਾਰਣ ਯਾਤਰੀ ਅਪਣੇ ਵਿਅਸਤ 40 ਸਾਲਾਂ ਦੌਰਾਨ ਹਜ਼ਾਰਾਂ ਪ੍ਰਕਾਸ਼ ਸਾਲਾਂ ਜਿੰਨੀ ਦੂਰ ਯਾਤਰਾ ਕਰ ਸਕਦਾ ਹੈ। ਜੇਕਰ ਸਪੇਸ-ਸ਼ਿਪ ਕਿਸੇ ਸਥਿਰ 1 g ਪ੍ਰਵੇਗ ਨਾਲ ਪ੍ਰਵੇਗਿਤ ਹੁੰਦਾ ਹੋਵੇ (ਅਪਣੀ ਖੁਦ ਦੀ ਰੈਫਰੈਂਸ ਫਰੇਮ ਅੰਦਰ), ਤਾਂ ਇਹ 354 ਦਿਨਾਂ ਬਾਦ, ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਤੋਂ ਜਰਾ ਘੱਟ ਸਪੀਡ ਤੱਕ ਦੀ ਸਪੀਡ ਪ੍ਰਾਪਤ ਕਰ ਲਵੇਗਾ (ਧਰਤੀ ਉੱਤੇ ਕਿਸੇ ਔਬਜ਼ਰਵਰ ਦੇ ਹਿਸਾਬ ਨਾਲ), ਅਤੇ ਟਾਈਮ ਡਿਲੇਸ਼ਨ, ਸੂਰਜੀ ਮੰਡਲ ਦੇ ਰੈਫਰੈਂਸ ਸਿਸਟਮ ਤੋਂ ਦੇਖੇ ਜਾਣ ਤੇ ਧਰਤੀ ਦੇ ਸਾਲਾਂ ਦੇ ਹਜ਼ਾਰਾਂ ਗੁਣਾਂ ਜਿਆਦਾ ਉਸਦੇ ਜੀਵਨਕਾਲ ਨੂੰ ਵਧਾ ਦੇਵੇਗੀ, ਪਰ ਯਾਤਰੀ ਦਾ ਸਾਹਮਣਾ ਕੀਤਾ ਜਾਣ ਵਾਲਾ ਜੀਵਨਕਾਲ ਇਸਤਰਾਂ ਨਹੀਂ ਬਦਲੇਗਾ। ਜੇਕਰ ਯਾਤਰੀ ਧਰਤੀ ਉੱਤੇ ਵਾਪਿਸ ਆ ਜਾਂਦਾ ਹੈ ਤਾਂ, ਧਰਤੀ ਦੇ ਭਵਿੱਖ ਵਿੱਚ ਹਜ਼ਾਰਾਂ ਸਾਲਾਂ ਅੱਗੇ ਉਤਰੇਗਾ। ਉਸਦੀ ਸਪੀਡ ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਤੋਂ ਜਿਆਦਾ ਹੁੰਦੀ ਨਹੀਂ ਨਾਪੀ ਜਾਵੇਗੀ, ਪਰ ਯਾਤਰਾ ਦੀ ਉਸਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਬ੍ਰਹਿਮੰਡ ਦੀ ਲੰਬਾਈ ਵਿੱਚ ਇੱਕ ਕਮੀ ਨਜ਼ਰ ਆਏਗੀ। ਅਤੇ ਜਿਉਂ ਹੀ ਯਾਤਰੀ ਧਰਤੀ ਉੱਤੇ ਪਰਤਦਾ ਹੈ, ਧਰਤੀ ਯਾਤਰੀ ਨਾਲ਼ੋਂ ਬਹੁਤ ਜਿਆਦਾ ਸਮਾਂ ਅਨੁਭਵ ਕਰਦੀ ਲੱਗੇਗੀ। ਇਸਲਈ, ਭਾਵੇਂ ਉਸਦੀ (ਸਧਾਰਨ) ਸਪੀਡ ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ c ਤੋਂ ਨਹੀਂ ਵਧ ਸਕਦੀ, ਤਾਂ ਵੀ ਚਾਰ-ਵਿਲੌਸਿਟੀ (ਉਸਦੇ ਸਹੀ, ਯਾਨਿ ਕਿ, ਸਾਹਮਣਾ ਕੀਤੇ ਜਾਣ ਵਾਲੇ ਸਮੇਂ ਦੁਆਰਾ ਵੰਡੀ ਗਈ ਧਰਤੀ ਦੁਆਰਾ ਦੇਖੀ ਗਈ ਦੂਰੀ) c ਤੋਂ ਕਿਤੇ ਜਿਆਦਾ ਹੋ ਸਕਦੀ ਹੈ। ਇਹ ਮਿਊਔਨਾਂ ਦੇ ਆਂਕੜਾਤਮਿਕ ਅਧਿਐਨ ਵਿੱਚ ਦੇਖਿਆ ਗਿਆ ਹੈ, ਜੋ ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ c ਅਤੇ ਅਪਣੀ ਅੱਧੀ-ਜਿੰਦਗੀ (ਅਰਾਮ ਵਿੱਚ) ਦੇ ਗੁਣਨਫਲ ਜਿੰਨੀ ਸਪੀਡ ਨਾਲ ਯਾਤਰਾ ਕਰਦੇ ਹਨ, ਜੇਕਰ c ਦੇ ਨੇੜੇ ਗਤੀਸ਼ੀਲ ਹੋਣ।
ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਤੋਂ ਜਿਆਦਾ ਫੇਜ਼ ਵਿਲੌਸਿਟੀਆਂ
[ਸੋਧੋ]ਕਿਸੇ ਮਾਧਿਅਮ ਰਾਹੀਂ ਗੁਜ਼ਰਦੀ ਕਿਸੇ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਵੇਵ ਦੀ ਫੇਜ਼ ਵਿਲੌਸਿਟੀ, ਪ੍ਰਕਾਸ਼ ਦੀ ਵੈਕੱਮ ਵਿਲੌਸਿਟੀ c ਤੋਂ ਨਿਯਮਿਤ ਰੂਪ ਵਿੱਚ ਵਧ ਸਕਦੀ ਹੈ। ਉਦਾਹਰਨ ਦੇ ਤੌਰ 'ਤੇ, X-ਰੇਅ ਫ੍ਰੀਕੁਐਂਸੀਆਂ ਉੱਤੇ ਜਿਆਦਾਤਰ ਸ਼ੀਸ਼ਿਆਂ ਵਿੱਚ ਅਜਿਹਾ ਵਾਪਰਦਾ ਹੈ। ਫੇਰ ਵੀ, ਕਿਸੇ ਤਰੰਗ ਦੀ ਫੇਜ਼ ਵਿਲੌਸਿਟੀ ਕਿਸੇ ਇਕਲੌਤੀ ਫ੍ਰੀਕੁਐਂਸੀ ਉੱਤੇ ਤਰੰਗ ਦੇ ਕਿਸੇ ਸਿਧਾਂਤਿਕ ਇਕਲੌਤੀ-ਫ੍ਰੀਕੁਐਂਸੀ ਵਾਲੇ (ਸ਼ੁੱਧ ਤੌਰ 'ਤੇ ਮੋਨੋਕ੍ਰੋਮੈਟਿਕ) ਕੰਪੋਨੈਂਟ ਦੀ ਸੰਚਾਰਾਤਮਿਕ ਸਪੀਡ ਨਾਲ ਸਬੰਧਤ ਹੁੰਦੀ ਹੈ। ਅਜਿਹਾ ਕੋਈ ਵੇਵ-ਕੰਪੋਨੈਂਟ (ਤਰੰਗ-ਹਿੱਸਾ) ਜਰੂਰ ਹੀ ਸੀਮਾ ਅੰਦਰ ਅਨੰਤ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਸਥਿਰ ਐਂਪਲੀਟਿਊਡ (ਅਧਿਕਤਾ) ਵਾਲਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ (ਨਹੀਂ ਤਾਂ ਇਹ ਸ਼ੁੱਧ ਤੌਰ 'ਤੇ ਮੋਨੋਕ੍ਰੋਮੈਟਿਕ ਨਹੀਂ ਹੁੰਦਾ), ਇਸਲਈ ਕੋਈ ਵੀ ਸੂਚਨਾ ਨਹੀਂ ਢੋਅ ਸਕਦਾ। ਇਸਤਰਾਂ c ਤੋਂ ਉੱਪਰ ਵਾਲੀ ਫੇਜ਼-ਵਿਲੌਸਿਟੀ c ਤੋਂ ਉੱਪਰ ਵਾਲੀ ਵਿਲੌਸਿਟੀ ਵਾਲੇ ਸਿਗਨਲਾਂ ਦੇ ਸੰਚਾਰ ਵਾਲਾ ਅਰਥ ਨਹੀਂ ਰੱਖਦੀ।
ਪ੍ਰਕਾਸ਼ ਦੀ ਸਪੀਡ ਤੋਂ ਜਿਆਦਾ ਗਰੁੱਪ ਵਿਲੌਸਿਟੀਆਂ
[ਸੋਧੋ]ਕਿਸੇ ਤਰੰਗ (ਜਿਵੇਂ ਉਦਾਹਰਨ ਦੇ ਤੌਰ 'ਤੇ, ਇੱਕ ਲਾਈਟ ਬੀਮ) ਦੀ ਗਰੁੱਪ ਵਿਲੌਸਿਟੀ ਵੀ ਕੁੱਝ ਪ੍ਰਸਥਿਤੀਆਂ ਅੰਦਰ c ਤੋਂ ਵਧ ਸਕਦੀ ਹੈ। ਅਜਿਹੇ ਮਾਮਲਿਆਂ ਵਿੱਚ, ਜੋ ਉਸੇ ਵਕਤ ਵਿਸ਼ੇਸ਼ ਤੌਰ 'ਤੇ ਤੀਬਰਤਾ ਵਿੱਚ ਤੇਜ਼ੀ ਨਾਲ ਕਮੀ ਲਿਆ ਦਿੰਦੇ ਹਨ, ਕਿਸੇ ਇਕਲੌਤੀ ਕੰਪਨ ਦੇ ਪੈਕਟ ਦਾ ਅਧਿਕਤਮ (ਮੈਗਜ਼ੀਮਮ) c ਤੋਂ ਉੱਪਰ ਦੀ ਵਿਲੌਸਿਟੀ ਨਾਲ ਯਾਤਰਾ ਕਰ ਸਕਦਾ ਹੈ। ਫੇਰ ਵੀ, ਅਜੇ ਤੱਕ ਇਹ ਪ੍ਰਸਥਿਤੀ ਵੀ c ਤੋਂ ਉੱਪਰ ਵਾਲੀ ਕਿਸੇ ਵਿਲੌਸਿਟੀ ਨਾਲ ਸਿਗਨਲਾਂ ਦਾ ਸੰਚਾਰ ਕਰਨ ਦਾ ਅਰਥ ਨਹੀਂ ਰੱਖਦੀ, ਭਾਵੇਂ ਬੇਸ਼ੱਕ ਸਿਗਨਲਾਂ ਨਾਲ ਪਲਸ ਅਧਿਕਤਮ ਸਬੰਧਤ ਕਰਨ ਲਈ ਮਜਬੂਰ ਹੋਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਬਾਦ ਵਾਲਾ ਸਬੰਧ ਗਲਤ ਜਾਣਕਾਰੀ ਦਿੰਦਾ ਸਾਬਤ ਹੋਇਆ ਹੈ, ਜਿਸਦਾ ਮੁਢਲੇ ਤੌਰ 'ਤੇ ਕਾਰਣ ਇਹ ਹੈ ਕਿ ਕਿਸੇ ਪਲਸ ਦੇ ਆਗਮਨ ਉੱਤੇ ਸੂਚਨਾ ਨੂੰ ਪਲਸ ਦੇ ਅਧਿਕਤਮ ਦੇ ਆਗਮਨ ਤੋਂ ਪਹਿਲਾਂ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਉਦਾਹਰਨ ਦੇ ਤੌਰ 'ਤੇ, ਜੇਕਰ ਕੋਈ ਮਕੈਨਿਜ਼ਮ, ਪਲਸ ਅਧਿਕਤਮ ਅਤੇ ਇਸਦੇ ਲਈ ਜਿਮੇਵਾਰ (ਸ਼ੋਰ) ਹਰੇਕ ਚੀਜ਼ ਨੂੰ ਕਮਜੋਰ ਕਰਕੇ ਕਿਸੇ ਪਲਸ ਦੇ ਪ੍ਰਮੁੱਖ ਹਿੱਸੇ ਦੇ ਸੰਪੂਰਣ ਸੰਚਾਰ ਦੀ ਆਗਿਆ ਦਿੰਦਾ ਹੈ, ਤਾਂ ਪਲਸ ਅਧਿਕਤਮ ਪ੍ਰਭਾਵੀ ਰੂਪ ਵਿੱਚ ਵਕਤ ਵਿੱਚ ਅੱਗੇ ਖਿਸਕ ਜਾਂਦਾ ਹੈ, ਜਦੋਂਕਿ ਪਲਸ ਉੱਤੇ ਦੀ ਸੂਚਨਾ ਇਸ ਪ੍ਰਭਾਵ ਤੋਂ ਬਗੈਰ c ਤੋਂ ਤੇਜ਼ ਨਹੀਂ ਆਉਂਦੀ। ਫੇਰ ਵੀ, ਵੈਕੱਮ (ਬਗੈਰ ਕਮਜੋਰੀ) ਵਿੱਚ ਗੌਸ਼ੀਅਨ ਬੀਮ ਦੇ ਕੁੱਝ ਹਿੱਸਿਆਂ ਵਿੱਚ ਗਰੁੱਪ ਵਿਲੌਸਿਟੀ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਹੋ ਸਕਦੀ ਹੈ। ਡਿੱਫ੍ਰੈਕਸ਼ਨ (ਵਿਵ੍ਰਤਨ) ਇਹ ਪ੍ਰਭਾਵ ਪਾਉਂਦਾ ਹੈ ਕਿ ਪਲਸ ਦੀ ਅਧਿਕਤਮ ਚੋਟੀ (ਪੀਕ) ਜਿਆਦਾ ਤੇਜ਼ ਸੰਚਾਰਿਤ ਹੁੰਦੀ ਹੈ, ਜਦੋਂਕਿ ਸਾਰੇ ਦੀ ਸਾਰੀ ਪਾਵਰ ਇੰਝ ਨਹੀਂ ਸੰਚਾਰਿਤ ਹੁੰਦੀ।
ਬ੍ਰਹਿਮੰਡੀ ਫੈਲਾਓ
[ਸੋਧੋ]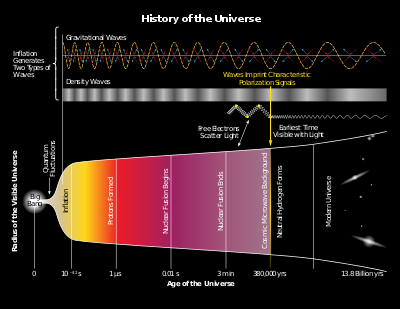
ਖਗੋਲਭੌਤਿਕੀ ਨਿਰੀਖਣ
[ਸੋਧੋ]ਕੁਆਂਟਮ ਮਕੈਨਿਕਸ
[ਸੋਧੋ]ਹਾਰਟਮੈਨ ਪ੍ਰਭਾਵ
[ਸੋਧੋ]ਕੈਸੀਮਿਰ ਪ੍ਰਭਾਵ
[ਸੋਧੋ]EPR ਪਹੇਲੀ
[ਸੋਧੋ]ਦੇਰੀ ਨਾਲ ਕੀਤੀ ਚੋਣ ਵਾਲਾ ਕੁਆਂਟਮ ਇਰੇਜ਼ਰ
[ਸੋਧੋ]ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਸੰਚਾਰ-ਵਿਵਸਥਾ
[ਸੋਧੋ]ਸਪੱਸ਼ਟੀਕਰਨ
[ਸੋਧੋ]ਹੋਰ ਤੇਜ਼ ਪ੍ਰਕਾਸ਼ (ਕੈਸੀਮਿਰ ਵੈਕੱਮ ਅਤੇ ਕੁਆਂਟਮ ਟਨਲਿੰਗ)
[ਸੋਧੋ](ਸ਼ੁੱਧ) ਸਾਪੇਖਿਕਤਾ ਛੱਡ ਦਿਓ
[ਸੋਧੋ]ਸਪੇਸਟਾਈਮ ਵਿਗਾੜ
[ਸੋਧੋ]ਹੇਇਮ ਥਿਊਰੀ
[ਸੋਧੋ]1977 ਵਿੱਚ, ਹੇਇਮ ਥਿਊਰੀ ਉੱਤੇ ਇੱਕ ਪੇਪਰ ਨੇ ਸਿਧਾਂਤਬੱਧ ਕੀਤਾ ਕਿ ਕਿਸੇ ਉੱਚ-ਅਯਾਮੀ ਸਪੇਸ ਵਿੱਚ ਦਾਖਲ ਹੋਣ ਵਾਸਤੇ ਚੁੰਬਕੀ ਫੀਲਡਾਂ ਵਰਤਣ ਰਾਹੀਂ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਯਾਤਰਾ ਕਰਨੀ ਸੰਭਵ ਹੈ।
ਲੌਰੰਟਜ਼ ਸਮਿੱਟਰੀ ਉਲੰਘਣਾ
[ਸੋਧੋ]ਭੌਤਿਕੀ ਪੁਲਾੜ ਦੀਆਂ ਸੁਪਰਫਲੱਡ ਥਿਊਰੀਆਂ
[ਸੋਧੋ]ਨਿਊਟ੍ਰੀਨੋਆਂ ਦੀ ਉਡਾਨ ਦਾ ਵਕਤ
[ਸੋਧੋ]MINOS ਪ੍ਰਯੋਗ
[ਸੋਧੋ]ਓਪੇਰਾ (OPERA) ਨਿਊਟ੍ਰੀਨੋ ਐਨੋਮਲੀ
[ਸੋਧੋ]ਟੈਕਿਔਨ
[ਸੋਧੋ]ਜਨਰਲ ਰਿਲੇਟੀਵਿਟੀ
[ਸੋਧੋ]ਪ੍ਰਕਾਸ਼ ਦੀ ਬਦਲਣਯੋਗ ਸਪੀਡ
[ਸੋਧੋ]ਇਹ ਵੀ ਦੇਖੋ
[ਸੋਧੋ]ਨੋਟਸ
[ਸੋਧੋ]ਹਵਾਲੇ
[ਸੋਧੋ]ਬਾਹਰੀ ਲਿੰਕ
[ਸੋਧੋ]ਵਿਗਿਆਨਿਕ ਲਿੰਕ
[ਸੋਧੋ]ਪ੍ਰਸਤਾਵਿਤ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਤੇਜ਼ ਵਿਧੀਆਂ ਵਾਲੇ ਲਿੰਕ
[ਸੋਧੋ]- ↑ "BICEP2 2014 Results Release". National Science Foundation. 17 March 2014. Retrieved 18 March 2014.
{{cite web}}: Unknown parameter|authors=ignored (help) - ↑ Clavin, Whitney (17 March 2014). "NASA Technology Views Birth of the Universe". NASA. Retrieved 17 March 2014.
- ↑ Overbye, Dennis (17 March 2014). "Detection of Waves in Space Buttresses Landmark Theory of Big Bang". New York Times. Retrieved 17 March 2014.

