ਕੁਆਟ੍ਰਨੀਔਨ
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
ਕੁਆਟ੍ਰਨੀਔਨ ਗਣਿਤ ਵਿੱਚ ਇੱਕ ਨੰਬਰ ਸਿਸਟਮ ਹੁੰਦਾ ਹੈ ਜੋ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਤੱਕ ਫੈਲਦਾ ਹੈ। ਇਹ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਆਇਰਿਸ਼ ਗਣਿਤ ਸ਼ਾਸਤਰੀ ਵਿਲੀਅਮ ਰੋਵਨ ਹੈਮਿਲਟਨ ਦੁਆਰਾ 1843/੧੮੪੩ ਵਿੱਚ ਦਰਸਾਏ ਗਏ ਸਨ। ਅਤੇ ਤਿੰਨ-ਅਯਾਮੀ ਸਪੇਸ ਵਿੱਚ ਮਕੈਨਿਕਸ ਉੱਤੇ ਲਾਗੂ ਕੀਤੇ ਗਏ ਸਨ। ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦਾ ਇੱਕ ਗੁਣ ਇਹ ਹੈ ਕਿ ਦੋ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦਾ ਗੁਣਨਫਲ ਨੌਨ-ਕਮਿਉਟੇਟਿਵ ਹੁੰਦਾ ਹੈ। ਹੈਮਿਲਟਨ ਨੇ ਇੱਕ ਕੁਆਟ੍ਰਨੀਔਨ ਨੂੰ ਤਿੰਨ-ਅਯਾਮੀ ਸਪੇਸ ਵਿੱਚ ਦੋ ਨਿਰਦੇਸ਼ਿਤ ਰੇਖਾਵਾਂ ਦੇ ਕੋਸ਼ੰਟ (ਗੁਣਕ) ਦੇ ਤੌਰ ਤੇ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂ ਦੋ ਵੈਕਟਰਾਂ ਦੇ ਕੋਸ਼ੰਟ ਦੇ ਤੌਰ ਤੇ ਬਰਾਬਰ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ।
ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀ ਵਰਤੋ ਸਿਧਾਂਤਕ ਅਤੇ ਉਪਯੋਗਿਕ ਗਣਿਤ ਦੋਹਾਂ ਵਿੱਚ ਹੁੰਦੀ ਹੈ, ਖਾਸ ਕਰਕੇ ਤਿੰਨ-ਅਯਾਮੀ ਰੋਟੇਸ਼ਨਾਂ ਵਾਲੀਆਂ ਕੈਲਕੁਲੇਸ਼ਨਾਂ ਲਈ ਜਿਹਨਾਂ ਵਿੱਚ ਤਿੰਨ ਅਯਾਮੀ ਕੰਪਿਊਟਰ ਗ੍ਰਾਫਿਕਸ, ਕੰਪਿਊਟਰ ਵਿਜ਼ਨ ਅਤੇ ਕ੍ਰਿਸਟੈੱਲੋਗ੍ਰਾਫਿਕ ਟੈਕਸਚਰ ਵਿਸ਼ਲੇਸ਼ਣ ਸ਼ਾਮਿਲ ਹਨ। ਪ੍ਰੈਕਟੀਕਲ ਐਪਲੀਕੇਸ਼ਨਾਂ (ਵਿਵਹਾਰਿਕ ਉਪਯੋਗਾਂ) ਵਿੱਚ, ਇਹਨਾਂ ਨੂੰ ਹੋਰ ਤਰੀਕਿਆਂ ਦੇ ਨਾਲ ਨਾਲ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਜਿਵੇਂ ਇਲੁਰ ਐਂਗਲ ਅਤੇ ਰੋਟੇਸ਼ਨ ਮੈਟ੍ਰੀਸੀਜ਼, ਜਾਂ ਇਹਨਾਂ ਦੇ ਬਦਲੇ ਵਿੱਚ, ਉਪਯੋਗ ਤੇ ਅਧਾਰਿਤ ਵਰਤੋ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ।
ਮਾਡਰਨ ਗਣਿਤਿਕ ਭਾਸ਼ਾ ਵਿੱਚ, ਕੁਆਟ੍ਰਨੀਔਨ ਵਾਸਤਵਿਕ ਨੰਬਰਾਂ ਉੱਤੇ ਇੱਕ ਚਾਰ-ਅਯਾਮੀ ਸਹਿਯੋਗੀ ਨੌਰਮਡ ਡਿਵੀਜ਼ਨ ਅਲਜਬਰਾ ਰਚਦੇ ਹਨ, ਅਤੇ ਇਸ ਕਰਕੇ ਇਹਨਾਂ ਦੀ ਇੱਕ ਡੋਮੇਨ ਹੁੰਦੀ ਹੈ। ਦਰਅਸਲ, ਕੁਆਟ੍ਰਨੀਔਨ ਪਹਿਲਾ ਖੋਜਿਆ ਗਿਆ ਨੌਨ-ਕਮਿਉਟੇਟਿਵ ਡਿਵੀਜ਼ਨ ਅਲਜਬਰਾ ਸੀ। ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਅਲਜਬਰੇ ਨੂੰ ਅਕਸਰ H (ਹੈਮਿਲਟਨ ਸ਼ਬਦ ਲਈ) ਨਾਲ ਲਿਖਿਆ ਜਾਂਦਾ ਹੈ, ਜਾਂ ਬਲੈਕਬੋਰਡ ਮੋਟੇ ਅੱਖਰ (Unicode U+210D, ℍ) ਰਾਹੀਂ ਲਿਖਿਆ ਜਾਂਦਾ ਹੈ। ਇਹ ਕਲਿੱਫੋਰਡ ਅਲਜਬਰਾ ਸ਼੍ਰੇਣੀਵੰਡ Cℓ0,2(R) ≅ Cℓ03,0(R) ਰਾਹੀਂ ਵੀ ਪ੍ਰਾਪਤ ਹੋ ਜਾਂਦਾ ਹੈ। ਫ੍ਰੋਬਿਨੀਅਸ ਥਿਊਰਮ ਮੁਤਾਬਿਕ, ਅਲਜਬਰਾ H ਅਵਲੋਕਨ ਮਾਮਲੇ ਵਿੱਚ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਸਥਾਨ ਰੱਖਦਾ ਹੈ, ਇਹ ਇੱਕ ਸਹੀ ਸਬ-ਰਿੰਗ ਦੇ ਤੌਰ ਤੇ ਵਾਸਤਵਿਕ ਨੰਬਰ ਰੱਖਣ ਵਾਲੇ ਸਿਰਫ ਦੋ ਸੀਮਤ-ਅਯਾਮੀ ਡਿਵੀਜ਼ਨ ਰਿੰਗਾਂ ਵਿੱਚੋਂ ਇੱਕ ਹੈ, ਦੂਜਾ ਰਿੰਗ ਕੰਪਲੈਕਸ ਨੰਬਰ ਹਨ। ਇਹਨਾਂ ਰਿੰਗਾਂ ਨੂੰ ਯੁਕਿਲਡਨ ਹੁਰਵਿਟਜ਼ ਅਲਜਬਰੇ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਜਿਹਨਾਂ ਵਿੱਚੋਂ ਕੁਆਟ੍ਰਨੀਔਨ ਸਭ ਤੋਂ ਵੱਡਾ ਐਸੋਸੀਏਟਿਵ ਅਲਜਬਰਾ ਹੈ।
ਇਸਲਈ ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ 3-ਸਫੀਅਰ S3 ਉੱਤੇ ਕਿਸੇ ਗਰੁੱਪ ਬਣਤਰ ਦੀ ਇੱਕ ਚੋਣ ਦੇ ਰੂਪ ਵਿੱਚ ਸੋਚਿਆ ਜਾ ਸਕਦਾ ਹੈ ਜੋ ਗਰੁੱਪ Spin(3) ਦਿੰਦੇ ਹਨ, ਜੋ SU(2) ਪ੍ਰਤਿ ਆਇਸੋਮੌਰਫਿਕ ਹੁੰਦਾ ਹੈ ਅਤੇ SU(3) ਦੇ ਬ੍ਰਹਿਮੰਡੀ ਕਵਰ ਪ੍ਰਤਿ ਵੀ ਆਇਸੋਮੌਰਫਿਕ ਹੁੰਦਾ ਹੈ।
ਪਰਿਭਾਸ਼ਾ
[ਸੋਧੋ]ਇੱਕ ਸੈੱਟ ਦੇ ਰੂਪ ਵਿੱਚ, ਕੁਆਟ੍ਰਨੀਔਨ H, ਵਾਸਤਵਿਕ ਨੰਬਰਾਂ ਉੱਤੇ ਇੱਕ ਚਾਰ-ਅਯਾਮੀ ਵੈਕਟਰ-ਸਪੇਸ R4 ਬਰਾਬਰ ਹਨ। H ਦੇ ਤਿੰਨ ਓਪਰੇਸ਼ਨ ਹਨ: ਜੋੜ, ਸਕੇਲਰ ਗੁਣਨਫਲ , ਅਤੇ ਕੁਆਟ੍ਰਨੀਔਨ ਗੁਣਨਫਲ। H ਦੇ ਦੋ ਐਲੀਮੈਂਟਾਂ ਦਾ ਜੋੜ, R4 ਦੇ ਐਲੀਮੈਂਟਾਂ ਦੇ ਤੌਰ ਤੇ ਉਹਨਾਂ ਦੇ ਜੋੜ ਦੇ ਰੂਪ ਵਿੱਚ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਇਸੇ ਤਰਾਂ, H ਦੇ ਕਿਸੇ ਐਲੀਮੈਂਟ ਦਾ ਕਿਸੇ ਵਾਸਤਵਿਕ ਨੰਬਰ ਨਾਲ ਗੁਣਨਫਲ R4 ਵਿੱਚ ਕਿਸੇ ਸਕੇਲਰ ਨਾਲ ਗੁਣਨਫਲ ਦੀ ਤਰਾਂ ਹੀ ਹੁੰਦਾ ਹੈ। H ਵਿਚਲੇ ਦੋ ਐਲੀਮੈਂਟਾਂ ਦੇ ਗੁਣਨਫਲ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰਨ ਲਈ R4 ਲਈ ਬੇਸਿਸ ਦੀ ਚੋਣ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ। ਇਸ ਬੇਸਿਸ ਦੇ ਐਲੀਮੈਂਟਾਂ ਨੂੰ ਰਿਵਾਜ ਦੇ ਤੌਰ ਤੇ 1, i, j, ਅਤੇ k ਲਿਖਿਆ ਜਾਂਦਾ ਹੈ। H ਦਾ ਹਰੇਕ ਐਲੀਮੈਂਟ ਇਹਨਾਂ ਬੇਸਿਸ ਐਲੀਮੈਂਟਾਂ ਦੇ ਕਿਸੇ ਲੀਨੀਅਰ (ਰੇਖਿਕ) ਮੇਲ (ਕੰਬੀਨੇਸ਼ਨ) ਦੇ ਰੂਪ ਵਿੱਚ ਨਿਰਾਲੇ ਤੌਰ ਤੇ ਲਿਖਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਜਿਵੇਂ a1 + bi + cj + dk, ਜਿੱਥੇ a, b, c, ਅਤੇ d ਵਾਸਤਵਿਕ ਨੰਬਰ ਹਨ। ਬੇਸਿਸ ਐਲੀਮੈਂਟ 1 ਨੂੰ H ਦਾ ਆਇਡੈਂਟਿਟੀ ਐਲੀਮੈਂਟ ਕਿਹਾ ਜਾਏਗਾ, ਜਿਸਦਾ ਅਰਥ ਹੈ ਕਿ 1 ਨਾਲ ਗੁਣਨਫਲ ਕਰਨ ਤੇ ਕੁੱਝ ਨਹੀਂ ਹੁੰਦਾ, ਅਤੇ ਇਸ ਕਾਰਨ ਕਰਕੇ, H ਦੇ ਐਲੀਮੈਂਟਾਂ ਨੂੰ ਆਮਤੌਰ ਤੇ ਬੇਸਿਸ ਐਲੀਮੈਂਟ 1 ਨੂੰ ਛੁਪਾ ਕੇ a + bi + cj + dk ਲਿਖਿਆ ਜਾਂਦਾ ਹੈ। ਇਸ ਬੇਸਿਸ ਦੇ ਦਿੱਤੇ ਹੋਣ ਤੇ, ਐਸੋਸੀਏਟਿਵ ਕੁਆਟ੍ਰਨੀਔਨ ਗੁਣਨਫਲ ਨੂੰ, ਬੇਸਿਸ ਐਲੀਮੈਂਟਾਂ ਦੇ ਗੁਣਨਫਲ ਨੂੰ ਪਹਿਲਾਂ ਪਰਿਭਾਸ਼ਿਤ ਕਰਕੇ ਅਤੇ ਫੇਰ ਡਿਸਟ੍ਰੀਬਿਊਟਿਵ ਨਿਯਮ ਵਰਤਕੇ ਬਾਕੀ ਸਾਰੇ ਗੁਣਨਫਲ ਪਰਿਭਾਸ਼ਿਤ ਕਰਕੇ, ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ।
ਇਤਿਹਾਸ
[ਸੋਧੋ]
16 ਅਕਤੂਬਰ 1843 ਨੂੰ ਜਾ ਰਿਹਾ ਸੀ
ਤਾਂ ਪ੍ਰਤਿਭਾ ਦੀ ਝਲਕ ਵਿੱਚ ਉਸਨੇ
ਕੁਆਟ੍ਰਨੀਔਨ ਗੁਣਨਫਲ
i2 = j2 = k2 = ijk = −1
ਲਈ ਫਾਰਮੂਲਾ ਖੋਜਿਆ
ਅਤੇ ਇਸ ਬਰਿੱਜ ਦੇ
ਇੱਕ ਪੱਥਰ ਉੱਤੇ ਇਸ ਨੂੰ ਉੱਕਰ ਦਿੱਤਾ
ਕੁਆਟ੍ਰਨੀਔਨ ਅਲਜਬਰਾ 1843 ਵਿੱਚ ਹੈਮਿਲਟਨ ਦੁਆਰਾ ਖੋਜਿਆ ਗਿਆ ਸੀ। ਇਸ ਕੰਮ ਤੋਂ ਪਹਿਲਾਂ ਅੱਗੇ ਆਉਣ ਵਾਲੇ ਮਹੱਤਵਪੂਰਨ ਕੰਮਾਂ ਵਿੱਚ ਇਲੁਰ ਦੀ ਚਾਰ-ਵਰਗ ਪਛਾਣ (ਫੋਰ-ਸਕੁਏਅਰ ਆਇਡੈਂਟਿਟੀ) (1748) ਅਤੇ ਓਲਿੰਡੇ ਰੋਡ੍ਰੀਜਿਉਸ ਦੀ ਚਾਰ ਪੈਰਾਮੀਟਰਾਂ ਰਾਹੀ ਜਨਰਲ ਰੋਟੇਸ਼ਨਾਂ ਦੀ ਪੈਰਾਮੀਟ੍ਰਾਇਜ਼ੇਸ਼ਨ (1840) ਸ਼ਾਮਲ ਹਨ, ਪਰ ਇਹਨਾਂ ਲੇਖਕਾਂ ਵਿੱਚੋਂ ਕਿਸੇ ਨੇ ਵੀ ਚਾਰ ਪੈਰਾਮੀਟਰਾਂ ਰੋਟੇਸ਼ਨਾਂ ਨੂੰ ਅਲਜਬਰੇ ਦੇ ਰੂਪ ਵਿੱਚ ਨਹੀਂ ਵਰਤਿਆ। ਕਾਰਲ ਫਰੈੱਡਰਿਸ਼ ਗਾਓੱਸ ਨੇ ਵੀ 1819 ਵਿੱਚ ਕੁਆਟ੍ਰਨੀਔਨ ਖੋਜੇ ਸਨ।, ਪਰ ਉਸਦਾ ਕੰਮ 1900 ਤੱਕ ਨਾ ਛਪਿਆ।
ਹੈਮੈਲਟਿਨ ਜਾਣਦਾ ਸੀ। ਕਿ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੀ ਕਿਸੇ ਪਲੇਨ ਵਿੱਚ ਵਿਆਖਿਆ ਬਿੰਦੂਆਂ ਦੇ ਰੂਪ ਵਿੱਚ ਹੋ ਸਕਦੀ ਹੈ, ਅਤੇ ਉਹ ਤਿੰਨ-ਅਯਾਮੀ ਸਪੇਸ ਵਿੱਚ ਬਿੰਦੂਆਂ ਲਈ ਇਹੀ ਕੁੱਝ ਕਰਨ ਦਾ ਤਰੀਕਾ ਖੋਜ ਰਿਹਾ ਸੀ। ਸਪੇਸ ਵਿੱਚ ਬਿੰਦੂਆਂ ਨੂੰ ਉਹਨਾਂ ਦੇ ਨਿਰਦੇਸ਼ਾਂਕਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਪ੍ਰਸਤੁਤੀ ਕੀਤਾ ਜਾ ਸਕਦਾ ਸੀ।, ਜੋ ਨੰਬਰਾਂ ਦੀ ਤਿੱਕੜੀ (ਟਰਿਪਲ) ਹੁੰਦੇ ਹਨ, ਅਤੇ ਕਈ ਸਾਲਾਂ ਤੋਂ ਉਹ ਜਾਣ ਚੁੱਕਿਆ ਸੀ ਕਿ ਨੰਬਰਾਂ ਦੇ ਟਰਿਪਲਾਂ ਨੂੰ ਕਿਵੇਂ ਜੋੜਨਾ ਅਤੇ ਘਟਾਉਣਾ ਹੈ। ਫੇਰ ਵੀ, ਹੈਮਿਲਟਨ ਇੱਕ ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਗੁਣਨਫਲ (ਮਲਟੀਪਲੀਕੇਸ਼ਨ) ਅਤੇ ਤਕਸੀਮ (ਡਿਵੀਜ਼ਨ) ਦੀ ਸਮੱਸਿਆ ਉੱਤੇ ਫਸਿਆ ਰਿਹਾ ਸੀ। ਉਹ ਇਹ ਨਹੀਂ ਦਰਸਾ ਸਕਿਆ ਕਿ ਸਪੇਸ ਵਿੱਚ ਦੋ ਬਿੰਦੂਆਂ ਦੇ ਨਿਰਦੇਸ਼ਾਂਕਾਂ ਦੇ ਕੋਸ਼ੰਟ ਨੂੰ ਕਿਵੇਂ ਕੱਢੀਦਾ ਹੈ।
ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਵਿੱਚ ਮਹਾਨ ਪ੍ਰਾਪਤੀ ਦਾ ਦਿਨ ਅੰਤ ਨੂੰ ਸੋਮਵਾਰ 16 ਅਕਤੂਬਰ 1843 ਦੇ ਸਮੇਂ ਡਬਲਿਨ ਵਿੱਚ ਆ ਹੀ ਗਿਆ, ਜਦੋਂ ਹੈਮਿਲਟਨ ਰੌਇਲ ਆਇਰਿਸ਼ ਅਕੈਡਮੀ ਲਈ ਰਸਤੇ ਵਿੱਚ ਜਾ ਰਿਹਾ ਸੀ, ਜਿੱਥੇ ਉਹ ਇੱਕ ਕੌਂਸਲ ਮੀਟਿੰਗ ਦੀ ਪ੍ਰਧਾਨਗੀ ਕਰਨ ਜਾ ਰਿਹਾ ਸੀ। ਜਿਉਂ ਹੀ ਉਹ ਅਪਣੀ ਪਤਨੀ ਨਾਲ ਰੌਇਲ ਨਹਿਰ ਕਿਨਾਰੇ ਰਸਤੇ ਉੱਤੋਂ ਤੁਰਿਆ, ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਪਿੱਛੇ ਦੇ ਸੰਕਲਪ ਉਸਦੇ ਦਿਮਾਗ ਵਿੱਚ ਅਕਾਰ ਲੈ ਰਹੇ ਸਨ। ਜਦੋਂ ਜਵਾਬ ਉਸ ਕੋਲ ਪ੍ਰਗਟ ਹੋ ਗਿਆ, ਹੈਮਿਲਟਨ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਲਈ ਇਹ ਫਾਰਮੂਲਾ, ਰੁਕ ਕੇ ਬਰੌਘਮ ਬਰਿੱਜ ਦੇ ਪੱਥਰ ਉੱਤੇ ਨਕਾਸ਼ੀ ਕਰਨ ਤੋਂ ਨਾ ਹਟ ਸਕਿਆ,
i2 = j2 = k2 = ijk = −1,
ਅਗਲੇ ਦਿਨ, ਹੈਮਿਲਟਨ ਨੇ ਅਪਣੇ ਦੋਸਤ ਅਤੇ ਸਾਥੀ ਗਣਿਤ ਸ਼ਾਸਤਰੀ ਜੌਹਨ ਟੀ. ਗਰੇਵਜ਼ ਨੂੰ ਚਿੱਠੀ ਲਿਖੀ, ਜਿਸ ਵਿੱਚ ਉਸਦੀ ਖੋਜ ਲਈ ਅਗਵਾਈ ਕਰਨ ਵਾਲੀ ਸੋਚਾਂ ਦੀ ਲੜੀ ਦਰਸਾਈ ਗਈ ਸੀ। ਇਹ ਚਿੱਠੀ ਲੰਡਨ, ਐਡਿੰਬਰਘ, ਅਤੇ ਡਬਲਿਨ ਫਿਲੌਸਫੀਕਲ ਮੈਗਜ਼ੀਨ ਅਤੇ ਜਰਨਲ ਔਫ਼ ਸਾਇੰਸ, ਵੌਲੁਓਮ 15 (1844), ਪੀ ਪੀ 489-95 ਵਿੱਚ ਬਾਦ ਵਿੱਚ ਛਾਪਿਆ ਗਿਆ, ਹੈਮਿਲਟਨ ਨੇ ਕਿਹਾ ਅਤੇ ਇੱਥੇ ਮੈਨੂੰ ਇਹ ਸੰਕਲਪ ਪ੍ਰਗਟ ਹੋਇਆ ਕਿ ਸਾਨੂੰ ਜਰੂਰ ਹੀ , ਕਿਸੇ ਸਮਝ ਵਿੱਚ, ਟਰਿਪਲਾਂ ਨਾਲ ਕੈਲਕੁਲੇਟ ਕਰਨ ਦੇ ਮਕਸਦ ਲਈ ਸਪੇਸ ਦੇ ਇੱਕ ਚੌਥੇ ਅਯਾਮ ਨੂੰ ਮੰਨ ਲੈਣਾ ਚਾਹੀਦਾ ਹੈ…ਇੱਕ ਇਲੈਕਟ੍ਰਿਕ ਸਰਕਟ ਬੰਦ ਹੁੰਦਾ ਲੱਗਿਆ, ਅਤੇ ਇੱਕ ਚਿੰਗਾਰੀ ਅੱਗੇ ਝਲਕੀ।
ਗੁਣਨਫਲ ਦੇ ਇਹਨਾਂ ਨਿਯਮਾਂ ਨਾਲ ਹੈਮਿਲਟਨ ਨੇ ਕੁਆਡ੍ਰਪਲ ਨੂੰ ਇੱਕ ਕੁਆਟ੍ਰਨੀਔਨ ਦਾ ਨਾਮ ਦਿੱਤਾ, ਅਤੇ ਉਸਨੇ ਅਪਣੀ ਜਿੰਦਗੀ ਦਾ ਬਾਕੀ ਬਚਿਆ ਜਿਆਦਾਤਰ ਹਿੱਸਾ ਇਹਨਾਂ ਨੂੰ ਪੜਾਉਣ ਅਤੇ ਅਧਿਐਨ ਕਰਨ ਤੇ ਸਮਰਪਿਤ ਕੀਤਾ। ਹੈਮਿਲਟਨ ਦਾ ਵਰਤਾਓ ਅਜੋਕੇ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਨਾਲੋਂ ਜਿਆਦਾ ਰੇਖਾ ਗਣਿਤਿਕ ਸੀ, ਜਿਸਨੇ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀਆਂ ਅਲਜਬਰਿਕ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਉੱਤੇ ਜੋਰ ਦਿੱਤਾ। ਉਸਨੇ “ਕੁਆਟ੍ਰਨੀਔਨਿਸਟਾਂ” ਦੇ ਇੱਕ ਸਕੂਲ ਦੀ ਨੀਂਹ ਰੱਖੀ, ਅਤੇ ਕਈ ਕਿਤਾਬਾਂ ਵਿੱਚ ਉਸਨੇ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ ਪ੍ਰਸਿੱਧ ਕਰਨ ਦੇ ਯਤਨ ਕੀਤੇ। ਉਸਦੀਆਂ ਕਿਤਾਬਾਂ ਵਿੱਚੋਂ ਅੰਤਿਮ ਅਤੇ ਸਭ ਤੋਂ ਜਿਆਦਾ ਲੰਬੀ ਕਿਤਾਬ, ਐਲੀਮੈਂਟਸ ਔਫ ਕੁਆਟ੍ਰਨੀਔਨਜ਼, 800 ਪੰਨਿਆਂ ਵਾਲੀ ਕਿਤਾਬ ਸੀ।; ਜੋ ਉਸਦੀ ਮੌਤ ਤੋਂ ਕੁੱਝ ਸਮਾਂ ਬਾਦ ਹੀ ਛਾਪੀ ਗਈ ਸੀ।
ਹੈਮਿਲਟਨ ਦੇ ਦੁਨੀਆਂ ਤੋਂ ਚਲੇ ਜਾਣ ਤੋਂ ਬਾਦ, ਉਸਦੇ ਵਿਦਿਅਰਥੀ ਪੀਟਰ ਟੈਇਟ ਨੇ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀ ਮਸ਼ਹੂਰੀ ਜਾਰੀ ਰੱਖੀ। ਇਸ ਵਕਤ ਤੇ, ਡਬਲਿਨ ਵਿੱਚ ਕੁਆਟ੍ਰਨੀਔਨ ਇੱਕ ਜਰੂਰੀ ਪ੍ਰੀਖਿਆ ਵਿਸ਼ਾ ਸੀ। ਭੌਤਿਕ ਵਿਗਿਆਨ ਅਤੇ ਜੀਓਮੈਟਰੀ (ਰੇਖਾਗਣਿਤ) ਵਿੱਚ ਵਿਸ਼ੇ ਜੋ ਹੁਣ ਵੈਕਟਰਾਂ ਦੀ ਵਰਤੋ ਨਾਲ ਦਰਸਾਏ ਜਾਂਦੇ ਹੋਣਗੇ, ਜਿਵੇਂ ਸਪੇਸ ਵਿੱਚ ਕਾਇਨਾਮੈਟਿਕਸ ਅਤੇ ਮੈਕਸਵੈੱਲ ਸਮੀਕਰਨਾਂ, ਪੂਰੇ ਦੇ ਪੂਰੇ ਹੀ ਉਦੋਂ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਰਸਾਏ ਜਾਂਦੇ ਸਨ। ਇੱਥੋਂ ਤੱਕ ਕਿ ਇੱਕ ਪ੍ਰੋਫੈਸ਼ਨਲ ਰਿਸਰਚ ਸੰਸਥਾ “ਕੁਆਟ੍ਰਨੀਔਨ ਸੋਸਾਇਟੀ” ਵੀ ਸੀ।, ਜੋ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਅਤੇ ਹੋਰ ਹਾਈਪਰ-ਕੰਪਲੈਕਸ ਨੰਬਰ ਸਿਸਟਮਾਂ ਦੇ ਅਧਿਐਨ ਪ੍ਰਤਿ ਸਮਰਪਿਤ ਕੀਤੀ ਗਈ ਸੀ।
ਅੱਧੇ 1880 ਵੇਂ ਦਹਾਕੇ ਤੋਂ, ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ ਵੈਕਟਰ ਅਵਲੋਕਨ ਰਾਹੀਂ ਦਰਸਾਇਆ ਜਾਣ ਲੱਗਿਆ, ਜੋ ਜੋਸੀਆਹ ਵਿਲੀਅਰਡ ਗਿੱਬਜ਼, ਓਲੀਵਰ ਹੀਵਿਜ਼ਾਇਡ, ਅਤੇ ਹਰਮਨ ਵੌਨ ਹੈਲਮਹੋਲਟਜ਼ ਦੁਆਰਾ ਵਿਕਸਿਤ ਕੀਤੇ ਗਏ ਸਨ। ਵੈਕਟਰ ਵਿਸ਼ਲੇਸ਼ਣ ਨੇ ਇਸੇ ਚੀਜ਼ ਨੂੰ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀ ਤਰਾਂ ਦਰਸਾਇਆ, ਇਸਲਈ ਇਸਨੇ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਸਾਹਿਤ ਤੋਂ ਕੁੱਝ ਵਿਚਾਰ ਅਤੇ ਸ਼ਬਦਾਵਲੀ ਅਜ਼ਾਦੀ ਨਾਲ ਉਧਾਰੀ ਲਈ। ਫੇਰ ਵੀ, ਵੈਕਟਰ ਵਿਸ਼ਲੇਸ਼ਣ ਸੰਕਲਪਿਕ ਤੌਰ ਤੇ ਸਰਲਤਮ ਅਤੇ ਚਿੰਨਾਂ ਦੇ ਤੌਰ ਤੇ ਸਾਫ ਸੁਥਰਾ ਸੀ, ਅਤੇ ਅੰਤ ਨੂੰ ਕੁਆਟ੍ਰਨੀਔਨ ਗਣਿਤ ਅਤੇ ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ ਛੋਟੀ ਜਿਹੀ ਭੂਮਿਕਾ ਤੱਕ ਸੀਮਤ ਕੇ ਦੂਰ ਕਰ ਦਿੱਤੇ ਗਏ। ਇਸ ਪਰਿਵਰਤਨਕਾਲ (ਟਰਾਂਜ਼ੀਸ਼ਨ) ਦਾ ਸਾਈਡ-ਇੱਫੈਕਟ (ਬੁਰਾ-ਅਸਰ) ਇਹ ਹੈ ਕਿ ਹੈਮਿਲਟਨ ਦਾ ਕੰਮ ਕਈ ਅਜੋਕੇ ਪਾਠਕਾਂ ਲਈ ਸਮਝਣਾ ਕਠਿਨ ਹੈ। ਹੈਮਿਲਟਨ ਦੀਆਂ ਮੂਲ ਪਰਿਭਾਸ਼ਾਵਾਂ ਜਾਣੀਆਂ ਪਛਾਣੀਆਂ ਨਹੀਂ ਹਨ ਅਤੇ ਉਸਦਾ ਲਿਖਣ ਦਾ ਅੰਦਾਜ਼ ਬਹੁਤ ਜਿਆਦਾ ਸ਼ਬਦਾਂ ਵਾਲਾ ਸੀ ਅਤੇ ਸਮਝਣ ਲਈ ਕਠਿਨ ਸੀ।
ਫੇਰ ਵੀ, ਲੇਟ 20ਵੀਂ ਸਦੀ ਤੋਂ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੇ ਫੇਰ ਪੁਨਰਜੀਵਨ ਲਿਆ, ਮੁੱਖ ਤੌਰ ਤੇ ਸਪੈਸ਼ੀਅਲ (ਸਥਾਨਿਕ) ਰੋਟੇਸ਼ਨਾਂ ਦਰਸਾਉਣ ਵਿੱਚ ਇਹਨਾਂ ਦੀ ਵਰਤੋ ਕਾਰਨ। ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਰਾਹੀਂ ਰੋਟੇਸ਼ਨਾਂ ਦੀਆਂ ਪ੍ਰਸਤੁਤੀਆਂ, ਮੈਟ੍ਰਿਕਸਾਂ ਰਾਹੀਂ ਪ੍ਰਸਤੁਤੀਆਂ ਨਾਲੋਂ ਜਿਆਦਾ ਸੰਖੇਪ ਅਤੇ ਤੇਜ ਹਨ। ਇਸਦੇ ਨਾਲ ਹੀ, ਇਲੁਰ ਐਂਗਲਾਂ ਤੋਂ ਉਲਟ, ਇਹ ਜਿੰਬਲ ਲੌਕ ਲਈ ਸ਼ੱਕੀ ਨਹੀਂ ਹਨ। ਇਸ ਕਾਰਣ ਕਰਕੇ, ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ ਕੰਪਿਊਟਰ ਗ੍ਰਾਫਿਕਸ, ਕੰਪਿਊਟਰ ਵਿਜ਼ਨ, ਰੋਬੋਟਿਕਸ, ਕੰਟਰੋਲ ਥਿਊਰੀ, ਸਗਨਲ ਪ੍ਰੋਸੈੱਸਿੰਗ, ਐਟੀਟਿਊਡ ਕੰਟਰੋਲ, ਭੌਤਿਕ ਵਿਗਿਆਨ, ਬਾਇਓਇਨਫੌਰਮੇਟਿਕਸ, ਮੌਲੀਕਿਉਲਰ ਡਾਇਨਾਮਿਕਸ, ਕੰਪਿਊਟਰ ਸਿਮੁਲਟੇਸ਼ਨਜ਼, ਅਤੇ ਔਰਬਿਟਲ ਮਕੈਨਿਕਸ ਵਿੱਚ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ। ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਸ਼ਬਦਾਂ ਵਿੱਚ ਸਪੇਸਕ੍ਰਾਫਟ ਦੇ ਐਟੀਟਿਊਡ ਕੰਟਰੋਲ ਸਿਸਟਮਾਂ ਨੂੰ ਨਿਰਦੇਸ਼ਿਤ ਕਰਨ ਲਈ ਵਰਤੋ ਆਮ ਗੱਲ ਹੈ। ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੇ ਨੰਬਰ ਥਿਊਰੀ ਤੋਂ ਇੱਕ ਹੋਰ ਵਾਧਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਹੈ ਕਿਉਂਕਿ ਇਹਨਾ ਦੇ ਕੁਆਡ੍ਰੈਟਿਕ ਅਕਾਰਾਂ ਨਾਲ ਸਬੰਧ ਹੁੰਦੇ ਹਨ।
1989 ਤੋਂ, ਨੈਸ਼ਨਲ ਯੂਨੀਵਰਸਟੀ ਔਫ ਆਇਰਲੈਂਡ, ਮੇਨੂਥ ਦੇ ਗਣਿਤ ਵਿਭਾਗ ਨੇ ਇੱਕ ਤੀਰਥ-ਯਾਤਰਾ ਆਯੋਜਿਤ ਕੀਤੀ ਹੈ, ਜਿੱਥੇ ਵਿਗਿਆਨੀ (ਜਿਸ ਵਿੱਚ 2002 ਵਿੱਚ ਭੋਤਿਕ ਵਿਗਿਆਨੀ ਮੁਰੱਰੇ ਗੈਲ-ਮਾੱਨ, 2005 ਵਿੱਚ ਸਟੀਵਨ ਵੇਨਬਰਗ, ਅਤੇ 2003 ਵਿੱਚ ਗਣਿਤ ਸ਼ਾਸਤਰੀ ਐਂਡ੍ਰਿਊ ਵਾਈਲਜ਼) ਡੱਨਸਿੰਕ ਔਬਜ਼ਰਵੇਟਰੀ ਤੋਂ ਰੌਇਲ ਕਨਾਲ ਬਰਿੱਜ ਤੱਕ ਯਾਤਰਾ ਕਰਦੇ ਹਨ। ਹੈਮਿਲਟਨ ਦੀ ਨਕਾਸ਼ੀ ਹੁਣ ਦ੍ਰਿਸ਼ਟੀਯੋਗ ਨਹੀਂ ਰਹੀ।
ਭੌਤਿਕ ਵਿਗਿਆਨ ਉੱਤੇ ਇਤਿਹਾਸਿਕ ਪ੍ਰਭਾਵ
[ਸੋਧੋ]ਪੀ.ਆਰ ਗਿਰਾਰਡ ਦਾ ਲੇਖ “ਦੀ ਕੁਆਟ੍ਰਨੀਔਨ ਗਰੁੱਪ ਐਂਡ ਮਾਡਰਨ ਭੌਤਿਕ ਵਿਗਿਆਨ” ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀਆਂ ਕੁੱਝ ਭੂਮਿਕਾਵਾਂ ਦੀ ਚਰਚਾ ਕਰਦਾ ਹੈ। ਇਹ ਦਿਖਾਉਂਦਾ ਹੈ ਕਿ ਕਿਵੇਂ ਵਿਭਿੰਨ ਭੌਤਿਕੀ ਕੋਵੇਰੀਅੰਸ ਗਰੁੱਪ: SO(3), ਲੌਰੰਟਜ਼ ਗਰੁੱਪ, ਜਨਰਲ ਰਿਲੇਟੀਵਿਟੀ ਗਰੁੱਪ, ਕਲਿੱਫੋਰਡ ਅਲਜਬਰਾ SU(2), ਅਤੇ ਕਨਫਰਮਲ ਗਰੁੱਪ ਮਾਡਰਨ ਅਲਜਬਰੇ ਵਿੱਚ ਕੁਆਟ੍ਰਨੀਔਨ ਗਰੁੱਪ ਨਾਲ ਸਬੰਧਤ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ। ਗਿਰਾਰਡ ਨੇ ਗਰੁੱਪ ਪ੍ਰਸਤੁਤੀਆਂ ਦੀ ਚਰਚਾ ਅਤੇ ਕ੍ਰਿਸਟੈੱਲੋਗ੍ਰਾਫੀ ਦੇ ਕੁੱਝ ਸਪੇਸ ਗਰੁੱਪਾਂ ਦੀ ਪੇਸ਼ਕਾਰੀ ਨਾਲ ਸ਼ੁਰੂ ਕੀਤਾ। ਫੇਰ ਉਹ ਠੋਸ ਚੀਜ਼ਾਂ ਦੀ ਗਤੀ ਦੇ ਕਾਇਨਾਮੈਟਿਕਸ ਵੱਲ ਅੱਗੇ ਵਧਿਆ। ਇਸਤੋਂ ਬਾਦ ਉਸਨੇ ਸਪੈਸ਼ਲ ਰਿਲੇਟੀਵਿਟੀ ਦੇ ਲੌਰੰਟਜ਼ ਗਰੁੱਪ ਨੂੰ ਪ੍ਰਸਤੁਤ ਕਰਨ ਲਈ ਕੰਪਲੈਕਸ ਕੁਆਟ੍ਰਨੀਔਨਾਂ (ਬਾਇਕੁਆਟ੍ਰਨੀਔਨਾਂ) ਨੂੰ ਵਰਤਿਆ, ਜਿਸ ਵਿੱਚ ਥੌਮਸ ਪਰਸੈਸ਼ਨ ਸ਼ਾਮਿਲ ਸੀ। ਉਸਨੇ ਲੁਡਵਿਕ ਸਿਲਬਰਸਟਨ ਨਾਲ ਸ਼ੁਰੂ ਕਰਦੇ ਹੋਏ, ਪੰਜ ਵਿਦਵਾਨਾਂ ਦੀ ਉਦਾਹਰਨ ਦਿੱਤੀ, ਜਿਸਨੇ ਇੱਕ ਕੁਆਟ੍ਰਨੀਔਨ ਅਸਥਿਰਾਂਕ ਦੇ ਇੱਕ ਪੁਟੈਂਸ਼ਲ ਫੰਕਸ਼ਨ ਨੂੰ ਮੈਕਵੈੱਲ ਇਕੁਏਸ਼ਨਾਂ ਨੂੰ ਇੱਕ ਸਿੰਗਲ ਡਿੱਫਰੈਂਸ਼ੀਅਲ ਇਕੁਏਸ਼ਨ ਵਿੱਚ ਦਰਸਾਉਣ ਲਈ ਵਰਤਿਆ ਸੀ। ਜਨਰਲ ਰਿਲੇਟੀਵਿਟੀ ਨਾਲ ਸਬੰਧਤ, ਉਸਨੇ ਰੁੰਗੇ-ਲੈੱਨਜ਼ ਵੈਕਟਰ ਨੂੰ ਸਮਝਾਇਆ। ਉਸਨੇ ਬਾਇਕੁਆਟ੍ਰਨੀਔਨਾਂ (ਸਪਲਿੱਟ ਬਾਇਕੁਆਟ੍ਰਨੀਔਨਾਂ) ਦਾ ਨਾਮ ਕਲਿੱਫੋਰਡ ਅਲਜਬਰਾ ਦੀ ਉਦਾਹਰਨ ਵਜੋਂ ਲਿਆ। ਅੰਤ ਵਿੱਚ, ਇੱਕ ਬਾਇਕੁਆਟ੍ਰਨੀਔਨ ਦੇ ਰੈਸੀਪ੍ਰੋਕਲ (ਉਲਟ) ਨੂੰ ਲਾਗੂ ਕਰਦੇ ਹੋਏ, ਗਿਰਾਰਡ ਨੇ ਸਪੇਸਟਾਈਮ ਉੱਤੇ ਕਨਫਰਮਲ ਮੈਪਾਂ ਨੂੰ ਦਰਸਾਇਆ। ਪੰਜਾਹ ਹਵਾਲਿਆਂ ਵਿੱਚ, ਗਿਰਾਰਡ ਨੇ ਅਲੈਗਜ਼ੈਂਡਰ ਮੈਕਫਾਰਲੇਨ ਅਤੇ ਉਸਦੇ "ਕੁਆਟ੍ਰਨੀਔਨ ਸੋਸਾਇਟੀ" ਦੇ ਬੁਲੇਟਿਨ ਨੂੰ ਸ਼ਾਮਿਲ ਕੀਤਾ। 1999 ਵਿੱਚ, ਉਸਨੇ ਦਿਖਾਇਆ ਕਿ ਕਿਵੇਂ ਆਈਨਸਟਾਈਨ ਦੀਆਂ ਜਨਰਲ ਰਿਲੇਟੀਵਿਟੀ ਦੀਆਂ ਇਕੁਏਸ਼ਨਾਂ ਇੱਕ ਕਲਿੱਫੋਰਡ ਅਲਜਬਰੇ ਅੰਦਰ ਫਾਰਮੂਲਾਬੱਧ ਕੀਤੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ ਜੋ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨਾਲ ਸਿੱਧਾ ਜੁੜਿਆ ਹੁੰਦਾ ਹੈ।
ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਪ੍ਰਤਿ ਇੱਕ ਹੋਰ ਨਿੱਜੀ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਜੋਚਿਮ ਲੈਮਬੇਕ ਵੱਲੋਂ 1995 ਵਿੱਚ ਲਿਖਿਆ ਗਿਆ ਸੀ। ਉਸਨੇ ਅਪਣੇ ਲੇਖ “ਜੇਕਰ ਹੈਮਿਲਟਨ ਨੇ ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ ਪ੍ਰਸਿੱਧ ਕੀਤਾ ਹੁੰਦਾ’’ ਵਿੱਚ ਲਿਖਿਆ: “ਮੇਰਾ ਅਪਣਾ ਸ਼ੌਕ ਇੱਕ ਗਰੈਜੁਏਟ ਵਿਦਿਆਰਥੀ ਹੋਣ ਦੇ ਨਾਤੇ ਸਿਲਬਰਸਟਨ ਦੀ ਪੁਸਤਕ ਰਾਹੀਂ ਉੱਚਾ ਉੱਠਿਆ।” ਉਸਨੇ ਇਹ ਕਹਿੰਦੇ ਹੋਏ ਲੇਖ ਮੁਕਾਇਆ “ਮੈਂ ਜੋਰਦਾਰ ਤਰੀਕੇ ਨਾਲ ਵਿਸ਼ਵਾਸ ਕਰਦਾ ਹਾਂ ਕਿ ਜੋ ਲੋਕ ਸਿਧਾਂਤਕ ਭੌਤਿਕ ਵਿਗਿਆਨ ਦੇ ਕੁੱਝ ਪਹਿਲੂਆਂ ਨਾਲ ਅਪਣੇ ਆਪ ਦੀ ਜਾਣ ਪਛਾਣ ਕਰਵਾਉਣਾ ਚਾਹੁੰਦੇ ਹਨ ਉਹਨਾਂ ਸ਼ੁੱਧ ਗਣਿਤ ਸ਼ਾਸਤਰੀਆਂ ਲਈ ਕੁਆਟ੍ਰਨੀਔਨ ਇੱਕ ਸ਼ੌਰਟ-ਕੱਟ (ਅਸਾਨ ਰਸਤਾ) ਮੁੱਹਈਆ ਕਰਾ ਸਕਦੇ ਹਨ।”
ਗੁਣਨਫਲ
[ਸੋਧੋ]ਗੁਣਨਫਲ ਨਾਲ ਇਸ ਦਾ ਸੰਬੰਧ ਹੇਠਾਂ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ,
ਬੇਸਿਸ ਐਲੀਮੈਂਟਾਂ ਦਾ ਗੁਣਨਫਲ
[ਸੋਧੋ]ਹੇਠਾਂ ਲਿਖੀਆਂ ਆਇਡੈਂਟਿਟੀਆਂ H ਦੇ ਬੇਸਿਸ ਐਲੀਮੈਟਾਂ i, j, ਅਤੇ k ਦੇ ਸਾਰੇ ਸੰਭਵ ਗੁਣਨਫਲ ਨਿਰਧਾਰਿਤ ਕਰਦੀਆਂ ਹਨ।
- ,
ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, −1 = ijk ਦੇ ਦੋਹੇ ਪਾਸਿਆਂ ਨੂੰ ਸੱਜੇ ਪਾਸੇ k ਨਾਲ ਗੁਣਾ ਕਰਨ ਤੇ ਇਹ ਮਿਲਦਾ ਹੈ;
ਇਸੇ ਤਰੀਕੇ ਨਾਲ ਸਾਰੇ ਹੋਰ ਸੰਭਵ ਗੁਣਨਫਲ ਨਿਰਧਾਰਿਤ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ। ਜੋ ਇਹ ਨਤੀਜਾ ਦਿੰਦੇ ਹਨ;
ਜਿਸਨੂੰ ਇੱਕ ਅਜਿਹੀ ਸਾਰਣੀ ਬਣਾ ਕਰ ਲਿਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ਜਿਸਦੀਆਂ ਲੇਟਵੀਆਂ ਕਤਾਰਾਂ (ਰੋਆਂ) ਗੁਣਨਫਲ ਦਾ ਖੱਬਾ ਹਿੱਸਾ (ਫੈਕਟਰ) ਪ੍ਰਸਤੁਤੀ ਕਰਦੀਆਂ ਹੋਣ ਅਤੇ ਜਿਸਦੇ ਖੜਵੇਂ ਕਾਲਮ ਸੱਜਾ ਫੈਕਟਰ ਪ੍ਰਸਤੁਤੀ ਕਰਦੇ ਹੋਣ, ਜਿਵੇਂ ਇਸ ਆਰਟੀਕਲ ਦੇ ਉੱਪਰਲੇ ਪਾਸੇ ਦਿਖਾਇਆ ਗਿਆ ਹੈ।
ਗੁਣਨਫਲ ਦਾ ਗੈਰ-ਕ੍ਰਮ ਵਟਾਂਦਰਾ ਸਬੰਧ
[ਸੋਧੋ]| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
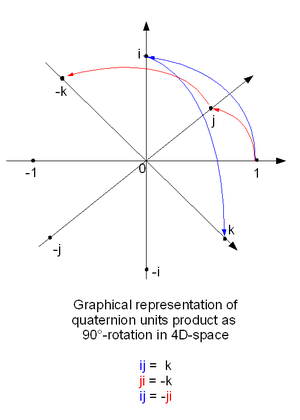
ਵਾਸਤਵਿਕ ਜਾਂ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੇ ਗੁਣਨਫਲ ਤੋਂ ਉਲਟ, ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦਾ ਗੁਣਨਫਲ ਕਮਿਉਟੇਟਿਵ ਨਹੀਂ ਹੁੰਦਾ। ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, ij = k ਹੁੰਦਾ ਹੈ ਜਦੋਂ ਕਿ ji = −k ਹੁੰਦਾ ਹੈ। ਗੁਣਨਫਲ ਦੀ ਨੌਨ-ਕਮਿਉਟੇਟੀਵਿਟੀ ਦੇ ਕੁੱਝ ਨਾ ਉਮੀਦ ਕੀਤੇ ਜਾਣ ਵਾਲੇ ਨਤੀਜੇ ਹਨ। ਜਿਹਨਾਂ ਵਿੱਚੋਂ ਇੱਕ ਇਹ ਹੈ ਕਿ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਉੱਤੇ ਪੌਲੀਨੌਮੀਅਲ ਸਮੀਕਰਨਾਂ ਪੌਲੀਨੌਮੀਅਲ ਦੀ ਡਿਗਰੀ ਤੋਂ ਜਿਆਦਾ ਵੱਖਰੇ ਹੱਲ ਰੱਖ ਸਕਦੀਆਂ ਹਨ। ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, ਸਮੀਕਰਨ z2 + 1=0 , ਦੇ ਅਨੰਤ ਤੌਰ ਤੇ ਕਈ ਹੱਲ z = bi + cj + dk ਹੁੰਦੇ ਹਨ ਜਿਹਨਾਂ ਵਿੱਚ b2 + c2 + d2 = 1 ਹੋਵੇ, ਤਾਂ ਜੋ ਇਹ ਹੱਲ, ਜ਼ੀਰੋ ਵਾਸਤਵਿਕ ਹਿੱਸੇ ਵਾਲੇ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀ ਤਿੰਨ-ਅਯਾਮੀ ਸਬਸਪੇਸ ਵਿੱਚਲੀ ਜ਼ੀਰੋ ਉੱਤੇ ਕੇਂਦ੍ਰਿਤ ਕਿਸੇ ਸਫੀਅਰ (ਗੋਲੇ) ਦੀ ਦੋ-ਅਯਾਮੀ ਸਤਹਿ ਉੱਤੇ ਟਿਕੇ ਹੋਣ। ਇਹ ਸਫੀਅਰ ਕੰਪਲੈਕਸ ਪਲੇਨ ਨੂੰ ਦੋ ਬਿੰਦੂਆਂ i ਅਤੇ -i ਉੱਤੇ ਕੱਟਦਾ ਹੈ।
ਤੱਥ ਕਿ ਕੁਆਟ੍ਰਨੀਔਨ ਗੁਣਨਫਲ ਕਮਿਉਟੇਟਿਵ ਨਹੀਂ ਹੁੰਦਾ, ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ ਕਿਸੇ ਸਖਤ ਤਿਰਛੀ ਫੀਲਡ ਦੀ ਇੱਕ ਅਕਸਰ ਹਵਾਲਾ ਦਿੱਤੀ ਜਾਣ ਵਾਲੀ ਉਦਾਹਰਨ ਬਣਾ ਦਿੰਦਾ ਹੈ।
ਹੈਮਿਲਟਨ ਗੁਣਨਫਲ
[ਸੋਧੋ]ਦੋ ਐਲੀਮੈਂਟਾਂ a1 + b1i + c1j + d1k ਅਤੇ a2 + b2i + c2j + d2k ਅਤੇ ਇਹਨਾਂ ਦਾ ਗੁਣਨਫਲ, ਜਿਸਨੂੰ ਹੈਮਿਲਟਨ ਗੁਣਨਫਲ (a1 + b1i + c1j + d1k) (a2 + b2i + c2j + d2k) ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਬੇਸਿਸ ਐਲੀਮੈਂਟਾਂ ਦੇ ਗੁਣਨਫਲ ਅਤੇ ਡਿਸਟ੍ਰੀਬਿਊਟਿਵ ਨਿਯਮ ਰਾਹੀਂ ਨਿਰਧਾਰਿਤ ਹੁੰਦਾ ਹੈ। ਡਿਸਟ੍ਰੀਨਬਿਊਟਿਵ ਨਿਯਮ ਗੁਣਨਫਲ ਦਾ ਵਿਸਥਾਰ ਕਰਨਾ ਸੰਭਵ ਬਣਾ ਦਿੰਦਾ ਹੈ ਤਾਂ ਜੋ ਇਹ ਬੇਸਿਸ ਐਲੀਮੈਂਟਾਂ ਦੇ ਗੁਣਨਫਲ ਦਾ ਜੋੜ ਹੁੰਦਾ ਹੈ। ਇਹ ਹੇਠਾ ਲਿਖੀਆਂ ਸਮੀਕਰਨਾ ਦਿੰਦਾ ਹੈ;
ਹੁਣ ਬੇਸਿਸ ਐਲੀਮੈਂਟਾਂ ਨੁੰ ਉੱਪਰ ਦੱਸੇ ਨਿਯਮਾਂ ਨੂੰ ਵਰਤਦੇ ਹੋਏ ਗੁਣਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਤਾਂ ਜੋ ਇਹ ਮਿਲ ਸਕੇ:
ਵਿਵਸਿਥ ਸੂਚੀ ਅਕਾਰ
[ਸੋਧੋ]H ਦੇ ਬੇਸਿਸ 1, i, j, k ਵਰਤਦੇ ਹੋਏ, H ਨੂੰ ਕੁਆਡ੍ਰਪਲਾਂ ਦੇ ਇੱਕ ਸੈੱਟ ਦੇ ਰੂਪ ਵਿੱਚ ਲਿਖਣਾ ਸੰਭਵ ਬਣ ਜਾਂਦਾ ਹੈ:
ਤਾਂ ਬੇਸਿਸ ਐਲੀਮੈਂਟ ਇਹ ਹੁੰਦੇ ਹਨ:
ਅਤੇ ਜੋੜ ਅਤੇ ਗੁਣਨਫਲ ਦੇ ਫਾਰਮੂਲੇ ਇਹ ਹੁੰਦੇ ਹਨ:
ਸਕੇਲਰ ਅਤੇ ਵੈਕਟਰ ਹਿੱਸੇ
[ਸੋਧੋ]a + 0i + 0j + 0k ਦੀ ਕਿਸਮ ਦਾ ਕੋਈ ਨੰਬਰ, ਜਿੱਥੇ a ਇੱਕ ਵਾਸਤਵਿਕ ਨੰਬਰ ਹੁੰਦਾ ਹੈ, ਨੂੰ ਵਾਸਤਵਿਕ ਨੰਬਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਅਤੇ ਕੋਈ ਵੀ ਨੰਬਰ ਜੋ 0 + bi + cj + dk ਕਿਸਮ ਦਾ ਹੋਵੇ, ਜਿੱਥੇ b, c, ਅਤੇ d ਵਾਸਤਵਿਕ ਨੰਬਰ ਹੋਣ, ਅਤੇ ਘੱਟੋ ਘੱਟ ਇਹਨਾਂ ਤਿੰਨਾਂ b, c, ਜਾਂ d ਵਿੱਚੋਂ ਕੋਈ ਵੀ ਇੱਕ ਨੰਬਰ ਗੈਰ-ਜ਼ੀਰੋ ਹੋਵੇ, ਤਾਂ ਇਸਨੂੰ ਸ਼ੁੱਧ ਕਾਲਪਨਿਕ ਨੰਬਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਜੇਕਰ a + bi + cj + dk ਕੋਈ ਕੁਆਟ੍ਰਨੀਔਨ ਹੋਵੇ, ਤਾਂ a ਨੂੰ ਇਸਦਾ ਸਕੇਲਰ ਹਿੱਸਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਤੇ bi + cj + dk ਨੂੰ ਇਸਦਾ ਵੈਕਟਰ ਹਿੱਸਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਦਾ ਸਕੇਲਰ ਹਿੱਸਾ ਹਮੇਸ਼ਾਂ ਹੀ ਵਾਸਤਵਿਕ ਹੁੰਦਾ ਹੈ, ਅਤੇ ਵੈਕਟਰ ਹਿੱਸਾ ਸ਼ੁੱਧ ਕਾਲਪਨਿਕ ਹੁੰਦਾ ਹੈ। ਭਾਵੇਂ ਹਰੇਕ ਕੁਆਟ੍ਰਨੀਔਨ ਨੂੰ ਇੱਕ ਚਾਰ-ਅਯਾਮੀ ਵੈਕਟਰ ਸਪੇਸ ਵਿੱਚ ਕਿਸੇ ਵੈਕਟਰ ਦੇ ਤੌਰ ਤੇ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਇਸਲਈ ਕਿਸੇ ਵੈਕਟਰ ਨੂੰ ਇੱਕ ਸ਼ੁੱਧ ਕਾਲਪਨਿਕ ਕੁਆਟ੍ਰਨੀਔਨ ਦੇ ਅਰਥਾਂ ਵਿੱਚ ਪਰਿਭਾਸ਼ਿਤ ਕਰਨਾ ਆਮ ਗੱਲ ਹੈ। ਇਸ ਪ੍ਰੰਪਰਾ ਨਾਲ ਇੱਕ ਵੈਕਟਰ, ਵੈਕਟਰ ਸਪੇਸ R3 ਦੇ ਕਿਸੇ ਐਲੀਮੈਂਟ ਬਰਾਬਰ ਹੀ ਹੁੰਦਾ ਹੈ।
ਫੇਰ ਵੀ, ਇਹ ਨੋਟ ਕਰਨਾ ਮਹੱਤਵਪੂਰਨ ਹੈ ਕਿ, ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਦਾ ਵੈਕਟਰ ਹਿੱਸਾ, ਦਰਅਸਲ, ਇੱਕ “ਐਕਸੀਅਲ” (ਧੁਰੇ ਵਾਲਾ) ਵੈਕਟਰ ਜਾਂ “ਸੂਡੋਵੈਕਟਰ” ਹੁੰਦਾ ਹੈ, ਕੋਈ ਸਧਾਰਣ ਜਾਂ “ਪੋਲਰ” ਵੈਕਟਰ ਨਹੀਂ ਹੁੰਦਾ, ਜਿਵੇਂ ਐੱਸ.ਐੱਲ. ਅਲਟਮਾੱਨ ਦੁਆਰਾ ਅਪਣੀ 1986 ਸੰਨ ਦੀ ਪੁਸਕਤ “ਰੋਟੇਸ਼ਨਜ਼,ਕੁਆਟ੍ਰਨੀਔਨਜ਼ ਐਂਡ ਡਬਲ ਗਰੁੱਪਸ” ਦੇ ਚੈਪਟਰ 12 ਵਿੱਚ ਪਹਿਲਾਂ ਸਿੱਧ ਕੀਤਾ ਗਿਆ ਸੀ। ਇੱਕ ਪੋਲਰ ਵੈਕਟਰ ਨੂੰ ਜਾਣਕਾਰੀ ਗੁਆਏ ਬਗੈਰ, ਇੱਕ ਸ਼ੁੱਧ ਕੁਆਟ੍ਰਨੀਔਨ ਰਾਹੀਂ ਕੈਲਕੁਲੇਸ਼ਨਾਂ (ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, ਜਦੋਂ ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਨੂੰ “ਸਿਮੀਲਰਟੀ ਟਰਾਂਸਫੌਰਮ” ਰਾਹੀਂ ਘੁਮਾਇਆ ਜਾਂਦਾ ਹੈ) ਵਿੱਚ ਪ੍ਰਸਤੁਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਪਰ ਇਹਨਾਂ ਦੋਵਾਂ ਦਰਮਿਆਨ ਗਲਤਫਹਿਮੀ ਨਹੀਂ ਪੈਦਾ ਕਰਨੀ ਚਾਹੀਦੀ। ਕਿਸੇ ਬਾਇਨਰੀ (180 ਡਿਗਰੀ) ਰੋਟੇਸ਼ਨ ਕੁਆਟ੍ਰਨੀਔਨ ਦਾ ਧੁਰਾ, ਅਜਿਹੇ ਮਾਮਲੇ ਵਿੱਚ, ਪ੍ਰਸਤੁਤ ਕੀਤੇ ਗਏ ਪੋਲਰ ਵੈਕਟਰ ਦੀ ਦਿਸ਼ਾ ਨਾਲ ਸਬੰਧਤ ਹੁੰਦਾ ਹੈ।
ਹੈਮਿਲਟਨ ਨੇ ਸ਼ੁੱਧ ਕਾਲਪਨਿਕ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ ਸੱਜੇ ਕੁਆਟ੍ਰਨੀਔਨ ਕਿਹਾ ਅਤੇ ਵਾਸਤਵਿਕ ਨੰਬਰਾਂ (ਜੋ ਜ਼ੀਰੋ ਵੈਕਟਰ ਹਿੱਸੇ ਵਾਲੇ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਤੌਰ ਤੇ ਲਏ ਜਾਂਦੇ ਹਨ) ਨੂੰ ਸਕੇਲਰ ਕੁਆਟ੍ਰਨੀਔਨ ਕਿਹਾ।
ਜੇਕਰ ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਨੂੰ ਇੱਕ ਸਕੇਲਰ ਹਿੱਸੇ ਅਤੇ ਇੱਕ ਵੈਕਟਰ ਹਿੱਸੇ ਵਿੱਚ ਵੰਡਣਾ ਕਰਨਾ ਹੋਵੇ, ਯਾਨਿ ਕਿ,
ਤਾਂ ਜੋੜ ਅਤੇ ਗੁਣਨਫਲ ਦੇ ਫਾਰਮੂਲੇ ਇਹ ਬਣ ਜਾਂਦੇ ਹਨ:
ਜਿੱਥੇ "•" ਡੌਟ ਪ੍ਰੋਡਕਟ ਹੈ ਅਤੇ "×" ਕਰੌਸ ਪ੍ਰੋਡਕਟ ਹੈ।
ਕੰਜੂਗੇਸ਼ਨ, ਨੌਰਮ ਅਤੇ ਰੈਸੀਪ੍ਰੋਕਲ
[ਸੋਧੋ]ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀ ਕੰਜੂਗੇਸ਼ਨ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੀ ਕੰਜੂਗੇਸ਼ਨ ਅਤੇ ਕਲਿੱਫੋਰਡ ਅਲਜਬਰੇ ਦੇ ਐਲੀਮੈਂਟਾਂ ਦੀ ਟਰਾਂਸਪੁਜ਼ੀਸਨ (ਜਿਸ ਨੂੰ ਰਿਵਰਸਲ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ) ਸਮਾਨ ਹੈ। ਇਸ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰਨ ਲਈ ਮੰਨ ਲਓ ਇੱਕ ਕੁਆਟ੍ਰਨੀਔਨ ਹੈ। q ਦਾ ਕੰਜੂਗੇਟ ਕੁਆਟ੍ਰਨੀਔਨ ਹੋਵੇਗਾ। ਇਸਨੂੰ q∗, q, qt, ਜਾਂ ਨਾਲ ਲਿਖਿਆ ਜਾਂਦਾ ਹੈ। ਕੰਜੂਗੇਸ਼ਨ ਇੱਕ ਉਤਪਤੀ ਹੁੰਦੀ ਹੈ, ਜਿਸਦਾ ਅਰਥ ਹੈ ਇਹ ਅਪਣੀ ਖੁਦ ਦੀ ਉਲਟ (ਇਨਵਰਸ) ਹੈ, ਇਸਲਈ ਕਿਸੇ ਐਲੀਮੈਂਟ ਨੂੰ ਦੋ ਵਾਰ ਕੰਜੂਗੇਟ ਕਰਨ ਨਾਲ ਮੂਲ ਐਲੀਮੈਂਟ ਫੇਰ ਵਾਪਿਸ ਆ ਜਾਂਦਾ ਹੈ। ਦੋ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਗੁਣਨਫਲ ਦਾ ਕੰਜੂਗੇਟ ਉਲਟੇ ਕ੍ਰਮ ਵਿੱਚ ਦੋ ਕੰਜੂਗੇਟਾਂ ਦੇ ਗੁਣਨਫਲ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ। ਯਾਨਿ ਕਿ, ਜੇਕਰ p ਅਤੇ q ਕੁਆਟ੍ਰਨੀਔਨ ਹੋਣ ਤਾਂ (pq)∗ = q∗p∗ ਹੁੰਦਾ ਹੈ, ਨਾ ਕਿ p∗q∗ ਹੋਵੇਗਾ ।
ਕੰਪਲੈਕਸ ਪਲੇਨ ਵਾਲੀ ਪ੍ਰਸਥਿਤੀ ਤੋਂ ਉਲਟ, ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਦੀ ਕੰਜੂਗੇਸ਼ਨ ਨੂੰ ਗੁਣਨਫਲ ਅਤੇ ਜੋੜ ਨਾਲ ਪੂਰੀ ਤਰਾਂ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ:
ਕੰਜੂਗੇਸ਼ਨ ਦੀ ਵਰਤੋਂ ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਦੇ ਸਕੇਲਰ ਅਤੇ ਵੈਕਟਰ ਹਿੱਸਿਆਂ ਨੂੰ ਵੱਖਰਾ ਕੱਢਣ ਲਈ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ। p ਦਾ ਸਕੇਲਰ ਹਿੱਸਾ (p + p∗) / 2 ਹੁੰਦਾ ਹੈ, ਅਤੇ p ਦਾ ਵੈਕਟਰ ਹਿੱਸਾ (p − p∗) / 2 ਹੁੰਦਾ ਹੈ।
ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਦੇ ਅਪਣੇ ਹੀ ਕੰਜੂਗੇਟ ਨਾਲ ਗੁਣਨਫਲ ਦੇ ਵਰਗਮੂਲ (ਸਕੁਏਅਰ ਰੂਟ) ਨੂੰ ਇਸਦਾ ਨੌਰਮ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਸਨੂੰ ||q|| ਲਿਖਿਆ ਜਾਂਦਾ ਹੈ (ਹੈਮਿਲਟਨ ਨੇ ਇਸ ਮਾਤਰਾ ਨੂੰ q ਦਾ ਟੈਂਸਰ ਕਿਹਾ ਸੀ, ਪਰ ਇਹ “ਟੈਂਸਰ” ਦੇ ਅਜੋਕੇ ਅਰਥ ਨੂੰ ਖਰਾਬ ਕਰਦਾ ਹੈ) ਫਾਰਮੂਲੇ ਵਿੱਚ, ਇਸਨੂੰ ਇਸ ਤਰਾਂ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ:
ਇਹ ਹਮੇਸ਼ਾਂ ਹੀ ਇੱਕ ਗੈਰ-ਨੈਗੇਟਿਵ ਵਾਸਤਵਿਕ ਨੰਬਰ ਹੁੰਦਾ ਹੈ, ਅਤੇ ਇਹ ਉਹੀ ਹੁੰਦਾ ਹੈ ਜੋ ਵੈਕਟਰ ਸਪੇਸ R4 ਦੇ ਤੌਰ ਤੇ ਲਿਆ ਜਾਣ ਵਾਲਾ ਯੁਕਿਲਡਨ ਨੌਰਮ ਹੁੰਦਾ ਹੈ। ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਨੂੰ ਇੱਕ ਵਾਸਤਵਿਕ ਨੰਬਰ ਨਾਲ ਗੁਣਾ ਕਰਨ ਤੇ ਇਸਦੇ ਨੌਰਮ ਨੂੰ ਨੰਬਰ ਦੇ ਸ਼ੁੱਧ ਮੁੱਲ ਨਾਲ ਨਾਪ ਦਿੰਦਾ ਹੈ। ਯਾਨਿ ਕਿ, ਜੇਕਰ α ਵਾਸਤਵਿਕ ਨੰਬਰ ਹੋਵੇ, ਤਾਂ
ਇਹ ਇਸ ਤੱਥ ਦਾ ਇੱਕ ਖਾਸ ਮਾਮਲਾ ਹੈ ਕਿ ਨੌਰਮ ਗੁਣਾ ਹੋਣ ਵਾਲਾ (ਮਲਟੀਲੀਲਕੇਟਿਵ) ਹੁੰਦਾ ਹੈ, ਜਿਸਦਾ ਅਰਥ ਹੈ ਕਿ; ਕਿਸੇ ਵੀ ਦੋ p ਅਤੇ q ਲਈ,
ਗੁਣਾ ਹੋਣ ਦੀ ਵਿਸ਼ੇਸ਼ਤਾ ਕਿਸੇ ਗੁਣਨਫਲ ਦੇ ਕੰਜੂਗੇਟ ਲਈ ਫਾਰਮੂਲੇ ਦਾ ਨਤੀਜਾ ਹੈ। ਇਸਦੇ ਬਦਲੇ ਵਿੱਚ ਇਸ ਆਇਡੈਂਟਿਟੀ ਤੋਂ ਪਤਾ ਚਲਦਾ ਹੈ ਕਿ,
(ਜਿੱਥੇ i ਆਮ ਕਾਲਪਨਿਕ ਯੂਨਿਟ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ) ਅਤੇ ਇਸਤਰਾਂ ਸਕੁਏਅਰ (ਵਰਗ) ਮੈਟ੍ਰਿਕਸਾਂ ਦੇ ਡਿਟ੍ਰਮੀਨੈਂਟਾਂ ਦੀ ਗੁਣਾ ਹੋਣ ਦੀ ਵਿਸ਼ੇਸ਼ਤਾ ਤੋਂ ਵੀ ਇਹੀ ਪਤਾ ਚਲਦਾ ਹੈ।
ਇਹ ਨੌਰਮ p ਅਤੇ q ਦਰਮਿਆਨ ਡਿਸਟੈਂਸ d(p, q) ਨੂੰ ਉਹਨਾਂ ਦੇ ਫਰਕ ਦੇ ਨੌਰਮ ਵਜੋਂ ਪਰਿਭਾਸ਼ਿਤ ਕਰਨਾ ਵੀ ਸੰਭਵ ਕਰਦਾ ਹੈ:
ਇਹ H ਨੂੰ ਇੱਕ ਮੈਟ੍ਰਿਕ ਸਪੇਸ ਬਣਾ ਦਿੰਦਾ ਹੈ। ਮੈਟ੍ਰਿਕ ਟੌਪੌਲੌਜੀ ਵਿੱਚ ਜੋੜ ਅਤੇ ਗੁਣਾ ਨਿਰਤੰਰ ਹੁੰਦੀ ਹੈ। ਸੱਚਮੁੱਚ, ਕਿਸੇ ਵੀ ਸਕੇਲਰ ਪੌਜ਼ੇਟਿਵ a ਲਈ, ਇਹ ਲਾਗੂ ਹੁੰਦਾ ਹੈ,
A ਨੂੰ ਮੁਕਾਉਣ ਲਈ ਨਿਰੰਤਰਤਾ ਜਾਰੀ ਰਹਿੰਦੀ ਹੈ। ਇਸੇ ਤਰਾਂ ਗੁਣਨਫਲ ਲਈ ਵੀ ਹੁੰਦਾ ਹੈ।
ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨ
[ਸੋਧੋ]ਇੱਕ ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨ ਇੱਕ ਨੌਰਮ 1 ਵਾਲਾ ਕੁਆਟ੍ਰਨੀਔਨ ਹੁੰਦਾ ਹੈ। ਕਿਸੇ ਗੈਰ-ਜ਼ੀਰੋ ਕੁਆਟ੍ਰਨੀਔਨ q ਨੂੰ ਉਸੇ ਦੇ ਨੌਰਮ ਨਾਲ ਤਕਸੀਮ ਕਰਨ ਤੇ ਇੱਕ ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨ Uq ਮਿਲਦਾ ਹੈ ਜਿਸਨੂੰ q ਦਾ ਵਰਸਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ:
ਹਰੇਕ ਕੁਆਟ੍ਰਨੀਔਨ ਦਾ ਇੱਕ ਪੋਲਰ ਡਿਕੰਪੋਜ਼ੀਸ਼ਨ q = ||q|| Uq ਹੁੰਦਾ ਹੈ।
ਕੰਜੂਗੇਸ਼ਨ ਅਤੇ ਨੌਰਮਾਂ ਦੀ ਵਰਤੋਂ ਕਿਸੇ ਗੈਰ-ਜ਼ੀਰੋ ਕੁਆਟ੍ਰਨੀਔਨ ਦੇ ਰੈਸੀਪ੍ਰੋਕਲ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰਨਾ ਸੰਭਵ ਕਰਦੀ ਹੈ। ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਦਾ ਉਸੇ ਦੇ ਰੈਸੀਪ੍ਰੋਕਲ ਨਾਲ ਗੁਣਨਫਲ 1 ਬਰਾਨਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ, ਅਤੇ ਉੱਪਰ ਦਰਸਾਈਆਂ ਮਾਨਤਾਵਾਂ ਤੋਂ ਭਾਵ ਹੈ ਕਿ ਅਤੇ (ਕਿਸੇ ਵੀ ਕ੍ਰਮ ਵਿੱਚ) ਦਾ ਗੁਣਨਫਲ 1 ਹੁੰਦਾ ਹੈ। ਇਸਤਰਾਂ, q ਦੇ ਰੈਸੀਪ੍ਰੋਕਲ ਨੂੰ ਇਸਤਰਾਂ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ:
ਇਹ ਦੋ ਕੁਆਟ੍ਰਨੀਔਨਾਂ p ਅਤੇ q ਨੂੰ ਦੋ ਹੋਰ ਵੱਖਰੇ ਤਰੀਕਿਆਂ (ਜਦੋਂ q ਗੈਰ-ਜ਼ੀਰੋ ਹੋਵੇ) ਨਾਲ ਤਕਸੀਮ ਕਰਨਾ ਸੰਭਵ ਕਰਦਾ ਹੈ। ਯਾਨਿ ਕਿ, ਇਹਨਾਂ ਦਾ ਕੋਸ਼ੰਟ p q−1 ਜਾਂ q−1p ਵਿੱਚੋਂ ਕੋਈ ਵੀ ਹੋ ਸਕਦਾ ਹੈ। ਧਾਰਨਾ p/q ਅਸਪਸ਼ਟ ਰਹਿੰਦੀ ਹੈ ਕਿਉਂਕਿ ਇਹ ਵਿਸ਼ੇਸ਼ ਤੌਰ ਤੇ ਨਹੀਂ ਦਰਸਾ ਪਾਉਂਦੀ ਕਿ q ਖੱਬੇ ਪਾਸੇ ਤਕਸੀਮ ਹੁੰਦਾ ਹੈ ਕਿ ਸੱਜੇ ਪਾਸੇ ਤਕਸੀਮ ਹੁੰਦਾ ਹੈ।
ਅਲਜਬਰਿਕ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ
[ਸੋਧੋ]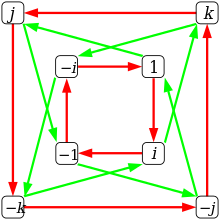
ਸਾਰੇ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦਾ ਸੈੱਟ H ਡਾਇਮੈਨਸ਼ਨ 4 ਵਾਲੀ ਵਾਸਤਵਿਕ ਨੰਬਰਾਂ ਉੱਤੇ ਇੱਕ ਵੈਕਟਰ ਸਪੇਸ ਹੁੰਦਾ ਹੈ। (ਤੁਲਨਾ ਦੇ ਤੌਰ ਤੇ, ਵਾਸਤਵਿਕ ਨੰਬਰਾਂ ਦੀ ਡਾਇਮੈਨਸ਼ਨ 1 ਹੁੰਦੀ ਹੈ, ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੀ ਡਾਇਮੈਨਸ਼ਨ 2 ਹੁੰਦੀ ਹੈ, ਅਤੇ ਔਕਟੋਨੀਅਨਾਂ ਦੀ ਡਾਇਮੈਨਸ਼ਨ 8 ਹੁੰਦੀ ਹੈ) ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦਾ ਗੁਣਨਫਲ, ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, ਵੈਕਟਰ ਜੋੜ ਉੱਤੇ ਐਸੋਸੀਏਟਿਵ ਅਤੇ ਡਿਸਟ੍ਰੀਬਿਊਟਿਵ ਹੁੰਦਾ ਹੈ, ਪਰ ਕਮਿਊਟੇਟਿਵ ਨਹੀਂ ਹੁੰਦਾ। ਇਸਲਈ, ਕੁਆਟ੍ਰਨੀਔਨ H ਵਾਸਤਵਿਕ ਨੰਬਰਾਂ ਉੱਤੇ ਇੱਕ ਨੌਨ-ਕਮਿਊਟੇਟਿਵ ਐਸੋਸੀਏਟਿਵ ਅਲਜਬਰਾ ਹੁੰਦੇ ਹਨ। ਭਾਵੇਂ H ਵਿੱਚ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੀਆਂ ਨਕਲਾਂ ਰੱਖੀਆਂ ਹੁੰਦੀਆਂ ਹਨ, ਫੇਰ ਵੀ ਇਹ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਉੱਤੇ ਐਸੋਸੀਏਟਿਵ ਅਲਜਬਰਾ ਨਹੀਂ ਹੁੰਦਾ।
ਕਿਉਂਕਿ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ ਤਕਸੀਮ ਕਰਨਾ ਸੰਭਵ ਹੁੰਦਾ ਹੈ, ਇਸਲਈ ਇਹ ਇੱਕ ਡਿਵੀਜ਼ਨ ਅਲਜਬਰਾ ਰਚਦੇ ਹਨ। ਗੁਣਨਫਲ ਦੀ ਨੌਨ-ਕਮਿਊਟੇਟੀਵਿਟੀ ਨੂੰ ਛੱਡ ਕੇ ਇਹ ਕਿਸੇ ਫੀਲਡ ਵਰਗੀ ਬਣਤਰ ਹੁੰਦੀ ਹੈ। ਵਾਸਤਵਿਕ ਨੰਬਰਾਂ ਉੱਤੇ ਸੀਮਤ-ਡਾਇਮੈਨਸ਼ਨਲ ਐਸੋਸੀਏਟਿਵ ਡਿਵੀਜ਼ਨ ਅਲਜਬਰੇ ਬਹੁਤ ਵਿਰਲੇ ਹੀ ਹੁੰਦੇ ਹਨ। ਫ੍ਰੋਬੀਨਿਉਸ ਥਿਊਰਮ ਦੱਸਦੀ ਹੈ ਕਿ ਅਜਿਹੇ ਤਿੰਨ ਹੁੰਦੇ ਹਨ: R,C, ਅਤੇ H। ਨੌਰਮ, ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦਾ ਇੱਕ ਨੌਰਮਡ ਅਲਜਬਰਾ ਬਣਾ ਦਿੰਦੇ ਹਨ, ਅਤੇ ਵਾਸਤਵਿਕ ਨੰਬਰਾਂ ਉੱਤੇ ਨੌਰਮਡ ਡਿਵੀਜ਼ਨ ਅਲਜਬਰੇ ਬਹੁਤ ਘੱਟ ਹੁੰਦੇ ਹਨ: ਹੁਰਵਿਟਜ਼ ਥਿਊਰਮ ਦੱਸਦੀ ਹੈ ਕਿ ਅਜਿਹੇ ਚਾਰ ਹੁੰਦੇ ਹਨ: R,C,H ਅਤੇ O (ਔਕਟੋਨੀਅਨ)। ਕੁਆਟ੍ਰਨੀਔਨ ਇੱਕ ਕੰਪੋਜ਼ੀਸ਼ਨ ਅਲਜਬਰੇ ਦੀ ਵੀ ਇੱਕ ਉਦਾਹਰਨ ਹੁੰਦੇ ਹਨ ਅਤੇ ਯੁਨਾਇਟਲ ਬਾਨਾਚ ਅਲਜਬਰੇ ਦੀ ਵੀ ਇੱਕ ਉਦਾਹਰਨ ਹਨ।
ਕਿਉਂਕਿ ਕਿਸੇ ਦੋ ਬੇਸਿਸ ਵੈਕਟਰਾਂ ਦਾ ਗੁਣਨਫਲ ਕਿਸੇ ਹੋਰ ਬੇਸਿਸ ਵੈਕਟਰ ਦਾ ਪਲਸ ਜਾਂ ਮਾਈਨਸ ਹੁੰਦਾ ਹੈ, ਸੈੱਟ {±1, ±i, ±j, ±k} ਗੁਣਨਫਲ ਅਧੀਨ ਇੱਕ ਗਰੁੱਪ ਰਚਦਾ ਹੈ। ਇਸ ਗਰੁੱਪ ਨੂੰ ਕੁਆਟ੍ਰਨੀਔਨ ਗਰੁੱਪ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਤੇ Q8 ਲਿਖਿਆ ਜਾਂਦਾ ਹੈ। ਕੁਆਟ੍ਰਨੀਔਨ, R[Q8] ਦਾ ਕੋਸ਼ੰਟ ਰਿੰਗ ਹੁੰਦੇ ਹਨ ਜੋ ਐਲੀਮੈਂਟਾਂ 1 + (−1), i + (−i), j + (−j), ਅਤੇ k + (−k) ਰਾਹੀਂ ਪੈਦਾ ਹੁੰਦੇ ਹਨ। ਇੱਥੇ ਹਰੇਕ ਅੰਤਰਾਂ ਵਿਚਲੀ ਪਹਿਲੀ ਰਕਮ ਬੇਸਿਸ ਐਲੀਮੈਂਟਾਂ 1, i, j, ਅਤੇ k ਵਿੱਚੋਂ ਇੱਕ ਹੁੰਦੀ ਹੈ, ਅਤੇ ਦੂਜੀ ਰਕਮ ਬੇਸਿਸ ਐਲੀਮੈਂਟਾਂ −1, −i, −j, ਅਤੇ –k ਵਿੱਚੋਂ ਇੱਕ ਹੁੰਦੀ ਹੈ, ਨਾ ਕਿ 1, i, j, ਅਤੇ k ਦੇ ਜੋੜ ਇਨਵਰਸ।
ਕੁਆਟ੍ਰਨੀਔਨ ਅਤੇ R3 ਦਾ ਰੇਖਾਗਣਿਤ
[ਸੋਧੋ]ਕਿਉਂਕਿ ਇੱਕ ਕੁਆਟ੍ਰਨੀਔਨ ਦਾ ਵੈਕਟਰ ਹਿੱਸਾ, R3 ਵਿੱਚ ਕੋਈ ਵੈਕਟਰ ਹੁੰਦਾ ਹੈ, ਇਸਲਈ R3 ਦਾ ਰੇਖਾ ਗਣਿਤ, ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀ ਅਲਜਬਰਿਕ ਬਣਤਰ ਤੋਂ ਪਤਾ ਚਲਦਾ ਹੈ। ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਸ਼ਬਦਾਂ ਵਿੱਚ ਵੈਕਟਰਾਂ ਉੱਤੇ ਕਈ ਓਪਰੇਸ਼ਨ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ, ਅਤੇ ਇਹੀ ਗੱਲ ਕੁਆਟ੍ਰਨੀਔਨ ਤਕਨੀਕਾਂ ਨੂੰ ਉੱਥੇ ਲਾਗੂ ਕਰਨਾ ਸੰਭਵ ਕਰਦੀ ਹੈ ਜਿੱਥੇ ਸਪੈਸ਼ੀਅਲ (ਸਥਾਨ ਸਬੰਧੀ) ਵੈਕਟਰ ਪੈਦਾ ਹੋਣ। ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, ਇਲੈਕਟ੍ਰੋਡਾਇਨਾਮਿਕਸ ਅਤੇ 3D ਕੰਪਿਊਟਰ ਗ੍ਰਾਫ਼ਿਕਸਾਂ ਵਿੱਚ ਇਹ ਸੱਚ ਹੁੰਦਾ ਹੈ।
ਇਸ ਸੈਕਸ਼ਨ ਦੇ ਬਾਕੀ ਹਿੱਸੇ ਲਈ, i, j, ਅਤੇ k , H ਦੇ ਕਾਲਪਨਿਕ ਬੇਸਿਸ ਵੈਕਟਰਾਂ ਅਤੇ R3 ਲਈ ਇੱਕ ਬੇਸਿਸ, ਦੋਵਾਂ ਨੂੰ ਦਰਸਾਉਣਗੇ। ਨੋਟ ਕਰੋ ਕਿ i ਨੂੰ –i ਨਾਲ, j ਨੂੰ –j ਨਾਲ, ਅਤੇ k ਨੂੰ –k ਨਾਲ ਬਦਲਣ ਤੇ ਕੋਈ ਵੈਕਟਰ ਅਪਣੇ ਜੋੜ-ਉਲਟ (ਐਡੀਟਵ ਇਨਵਰਸ ਜਾਂ ਨੈਗੈਟਿਵ) ਦਾ ਰੂਪ ਬਣ ਜਾਂਦਾ ਹੈ, ਇਸਲਈ ਕਿਸੇ ਵੈਕਟਰ ਦਾ ਐਡੀਟਵ ਇਨਵਰਸ, ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਦੇ ਤੌਰ ਤੇ ਉਸਦਾ ਕੰਜੂਗੇਟ ਹੀ ਹੁੰਦਾ ਹੈ। ਇਸ ਕਾਰਣ ਕਰਕੇ, ਕੰਜੂਗੇਸ਼ਨ ਨੂੰ ਕਦੇ ਕਦੇ ਸਪੈਸ਼ੀਅਲ ਇਨਵਰਸ (ਸਥਾਨਿਕ ਉਲਟਾਓ) ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।
ਦੋ ਕੁਆਟ੍ਰਨੀਔਨ p = b1i + c1j + d1k ਅਤੇ q = b2i + c2j + d2k ਚੁਣੋ। ਇਹਨਾਂ ਦਾ ਡੌਟ ਪ੍ਰੋਡਕਟ (ਅੰਦਰੂਨਿ ਗੁਣਨਫਲ) ਇਹ ਹੁੰਦਾ ਹੈ;
ਇਹpq∗, qp∗, p∗q, ਅਤੇ q∗p ਦੇ ਸਕੇਲਰ ਹਿੱਸਿਆਂ ਸਮਾਨ ਹੈ। (ਨੋਟ ਕਰੋ ਕਿ ਇਹਨਾਂ ਚਾਰੇ ਗੁਣਨਫਲਾਂ ਦੇ ਵੈਕਟਰ ਹਿੱਸੇ ਵੱਖਰੇ ਵੱਖਰੇ ਹਨ)। ਇਸਦਾ ਇਹ ਫਾਰਮੂਲਾ ਵੀ ਹੁੰਦਾ ਹੈ;
ਵਿਵਸਿਥ ਬੇਸਿਸ i, j, ਅਤੇ k ਰਾਹੀਂ ਨਿਰਧਾਰਿਤ ਕੀਤੀ ਦਿਸ਼ਾ ਦੇ ਸਾਪੇਖਿਕ p ਅਤੇ q ਦਾ ਕਰੌਸ ਪ੍ਰੋਡਕਟ (ਬਾਹਰੀ ਗੁਣਨਫਲ) ਇਹ ਹੁੰਦਾ ਹੈ;
(ਯਾਦ ਕਰੋ ਕਿ ਚਿੰਨ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਨ ਲਈ ਦਿਸ਼ਾ ਲਾਜ਼ਮੀ ਚੀਜ਼ ਹੈ) ਇਹ ਗੁਣਨਫਲ pq (ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਰੂਪ ਵਿੱਚ) ਦੇ ਵੈਕਟਰ ਹਿੱਸੇ ਦੇ ਸਮਾਨ ਹੈ, ਅਤੇ −q∗p∗ ਦੇ ਵੈਕਟਰ ਹਿੱਸੇ ਦੇ ਸਮਾਨ ਵੀ ਹੈ। ਇਸਦਾ ਇਹ ਫਾਰਮੂਲਾ ਵੀ ਹੁੰਦਾ ਹੈ;
ਦੋ ਕਾਲਪਨਿਕ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਕਮਿਉਟੇਟਰ [p, q] = pq – qp ਲਈ, ਇਹ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ;
ਸਰਵ ਸਧਾਰਣ ਤੌਰ ਤੇ, ਮੰਨ ਲਓ p ਅਤੇ q ਕੁਆਟ੍ਰਨੀਔਨ (ਸੰਭਵ ਤੌਰ ਤੇ ਗੈਰ-ਕਾਲਪਨਿਕ) ਹੋਣ, ਅਤੇ ਇੰਖ ਲਿਖੇ ਜਾਣ
ਜਿੱਥੇ p ਅਤੇ q ਦੇ, ps ਅਤੇ qsਸਕੇਲਰ ਹਿੱਸੇ ਹਨ, ਅਤੇ, and ਵੈਕਟਰ ਹਿੱਸੇ ਹਨ। ਤਾਂ ਸਾਡੇ ਕੋਲ ਇਹ ਫਾਰਮੂਲਾ ਹੁੰਦਾ ਹੈ;
ਇਹ ਸਾਬਤ ਕਰਦਾ ਹੈ ਕਿ ਕੁਆਟ੍ਰਨੀਔਨ ਗੁਣਨਫਲ ਦੀ ਨੌਨ-ਕਮਿਊਟੇਟੀਵਿਟੀ ਸ਼ੁੱਧ ਕਾਲਪਨਿਕ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਗੁਣਨਫਲ ਤੋਂ ਆਉਂਦੀ ਹੈ। ਇਹ ਗੱਲ ਇਹ ਵੀ ਸਾਬਤ ਕਰਦੀ ਹੈ ਕਿ ਦੋ ਕੁਆਟ੍ਰਨੀਔਨ ਸਿਰਫ ਤੇ ਸਿਰਫ ਤਾਂ ਹੀ ਕਮਿਊਟ ਕਰਦੇ ਹਨ (ਕ੍ਰਮ ਵਟਾਂਦਰਾ ਸਬੰਧ ਰੱਖਦੇ ਹਨ) ਜੇਕਰ ਉਹਨਾਂ ਦੇ ਵੈਕਟਰ ਹਿੱਸੇ ਕੋਲੀਨੀਅਰ (ਇੱਕੋ ਰੇਖਾ ਤੇ ਜਾਂ ਸਮਰੇਖਿਕ) ਹੋਣ।
ਤਿੰਨ-ਡਾਇਮੈਨਸ਼ਨਲ ਵੈਕਟਰਾਂ ਦੀ ਕੁਆਟ੍ਰਨੀਔਨ ਵਰਤੋ ਦੀ ਮਾਡਲਿੰਗ ਉੱਤੇ ਹੋਰ ਵਿਸਥਾਰਪੂਰਵਕ ਜਾਣਕਾਰੀ ਲਈ, ਦੇਖੋ "ਕੁਆਟ੍ਰਨੀਔਨ ਅਤੇ ਸਪੈਸ਼ੀਅਲ ਰੋਟੇਸ਼ਨ"। ਇੱਕ ਸੰਭਵ ਦ੍ਰਿਸ਼-ਚਿਤ੍ਰਣ ਐਂਡ੍ਰਿਊ ਜੇ. ਹੰਸਨ ਦੁਆਰਾ ਪੇਸ਼ ਕੀਤਾ ਗਿਆ ਸੀ। [1]
ਮੈਟ੍ਰਿਕਸ ਪ੍ਰਸਤੁਤੀ
[ਸੋਧੋ]ਜਿਵੇਂ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਨੂੰ ਮੈਟ੍ਰਿਕਸਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਪ੍ਰਸਤੁਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਉਸੇ ਤਰਾਂ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ ਵੀ ਪ੍ਰਸਤੁਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ ਮੈਟ੍ਰਿਕਸਾਂ ਦੀ ਤਰਾਂ ਪ੍ਰਸਤੁਤ ਕਰਨ ਦੇ ਘੱਟੋ ਘੱਟ ਦੋ ਅਜਿਹੇ ਤਰੀਕੇ ਹਨ ਕਿ ਕੁਆਟ੍ਰਨੀਔਨ ਜੋੜ ਅਤੇ ਗੁਣਾ ਮੈਟ੍ਰਿਕਸ ਜੋੜ ਅਤੇ ਮੈਟ੍ਰਿਕਸ ਗੁਣਨਫਲ ਨਾਲ ਸਬੰਧਤ ਹੁੰਦੀ ਹੈ। ਇੱਕ ਤਰੀਕਾ 2 × 2 ਕੰਪਲੈਕਸ ਮੈਟ੍ਰਿਕਸ ਵਰਤਣ ਦਾ ਹੈ, ਅਤੇ ਦੂਜਾ 4 × 4 ਵਾਸਤਵਿਕ ਮੈਟ੍ਰਿਕਸ ਵਰਤਣ ਦਾ ਹੈ। ਹਰੇਕ ਮਾਮਲੇ ਵਿੱਚ, ਦਿੱਤੀ ਜਾਣ ਵਾਲੀ ਪ੍ਰਸਤੁਤੀ ਰੇਖਿਕ ਤੌਰ ਤੇ ਸਬੰਧਤ ਪ੍ਰਸਤੁਤੀਆਂ ਦਾ ਇੱਕ ਪਰਿਵਾਰ ਹੁੰਦਾ ਹੈ। ਅਮੂਰਤ (ਅਬਸਟ੍ਰੈਕਟ) ਅਲਜਬਰੇ ਦੀ ਸ਼ਬਦਾਵਲੀ ਵਿੱਚ, ਇਹ H ਤੋਂ ਮੈਟ੍ਰਿਕਸ ਰਿੰਗਾਂ M(2, C) ਅਤੇ M(4, R) ਤੱਕ ਕ੍ਰਮਵਾਰ ਇੰਜੈਕਟਿਵ ਹੋਮੋਮੌਰਫਿਜ਼ਮਾਂ ਹੁੰਦੀਆਂ ਹਨ।
2 × 2 ਕੰਪਲੈਕਸ ਮੈਟ੍ਰਿਕਸ ਵਰਤਦੇ ਹੋਏ, ਕੁਆਟ੍ਰਨੀਔਨ a + bi + cj + dk ਨੂੰ ਇਸਤਰਾਂ ਪ੍ਰਸਤੁਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ;
ਇਸ ਪ੍ਰਸਤੁਤੀ ਦੀਆਂ ਹੇਠਾਂ ਲਿਖੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹਨ:
- b, c ਅਤੇ d ਵਿੱਚੋਂ ਕਿਸੇ ਦੋ ਨੂੰ ਜ਼ੀਰੋ ਹੋਣ ਲਈ ਮਜਬੂਰ ਕਰਨ ਤੇ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੀ ਇੱਕ ਪ੍ਰਸਤੁਤੀ ਪੈਦਾ ਹੁੰਦੀ ਹੈ। ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, c = d = 0 ਸੈੱਟ ਕਰਨ ਤੇ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੀ ਇੱਕ ਇੱਕ ਡਾਇਓਗਨਲ (ਤਿਰਛੀ) ਕੰਪਲੈਕਸ ਮੈਟ੍ਰਿਕਸ ਪ੍ਰਸਤੁਤੀ ਪੈਦਾ ਹੁੰਦੀ ਹੈ, ਅਤੇ b = d = 0 ਸੈੱਟ ਕਰਨ ਤੇ ਇੱਕ ਵਾਸਤਵਿਕ ਮੈਟ੍ਰਿਕਸ ਪ੍ਰਸਤੁਤੀ ਪੈਦਾ ਹੁੰਦੀ ਹੈ।
- ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਦਾ ਨੌਰਮ (ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਵਾਂਗ, ਇਸਦੇ ਕੰਜੂਗੇਟ ਨਾਲ ਗੁਣਨਫਲ ਦਾ ਵਰਗਮੂਲ) ਸਬੰਧਤ ਮੈਟ੍ਰਿਕਸ ਦੇ ਡਿਟ੍ਰਮੀਨੈਂਟ ਦਾ ਵਰਗਮੂਲ ਹੁੰਦਾ ਹੈ।
- ਪਾਬੰਧੀ ਰਾਹੀਂ ਇਹ ਪ੍ਰਸਤੁਤੀ ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਅਤੇ ਉਹਨਾਂ ਦੀ ਇਮੇਜ SU(2) ਦੇ ਸਬਗਰੁੱਪ ਦਰਮਿਆਨ ਇੱਕ ਆਇਸੋਮੌਰਫਿਜ਼ਮ ਪੈਦਾ ਕਰਦੀ ਹੈ। ਟੌਪੌਲੌਜੀ ਦੇ ਤੌਰ ਤੇ, ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨ 3-ਸਫੀਅਰ ਹੁੰਦੇ ਹਨ। ਤਾਂ ਜੋ ਛੁਪੀ ਹੋਈ SU(2) ਦੀ ਸਪੇਸ ਵੀ ਇੱਕ 3-ਸਫੀਅਰ ਹੁੰਦੀ ਹੈ। ਗਰੁੱਪ SU(2) ਕੁਆਂਟਮ ਮਕੈਨਿਕਸ ਵਿੱਚ ਸਪਿੱਨ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਮਹੱਤਵਪੂਰਨ ਹੈ; ਦੇਖੋ ਪੌਲੀ ਮੈਟ੍ਰਿਕਸ।
4 × 4 ਵਾਸਤਵਿਕ ਮੈਟ੍ਰਿਕਸ ਵਰਤਦੇ ਹੋਏ, ਇਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਨੂੰ ਇਸਤਰਾਂ ਲਿਖਿਆ ਜਾ ਸਕਦਾ ਹੈ;
ਜਿੱਥੇ ਤਿਰਛੇ-ਸਮਰੂਪ ਮੈਟ੍ਰਿਕਸ ਨਿਰਾਲੇ (ਯੁਨੀਕ) ਨਹੀਂ ਹਨ। ਦਰਅਸਲ, ਅਜਿਹੇ ਮੈਟ੍ਰਿਕਸਾਂ ਦੇ ਵੱਖਰੇ ਵੱਖਰੇ 48 ਵਿਵਸਿਥ ਸੈੱਟ ਮੌਜੂਦ ਹਨ। ਇਸ ਪ੍ਰਸਤੁਤੀ ਵਿੱਚ, ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਦਾ ਕੰਜੂਗੇਟ ਮੈਟ੍ਰਿਕਸ ਦੇ ਟਰਾਂਸਪੋਜ਼ ਨਾਲ ਸਬੰਧਤ ਹੁੰਦਾ ਹੈ। ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਦੇ ਨੌਰਮ ਦੇ ਵਰਗ ਦਾ ਵਰਗ (ਚੌਥੀ ਪਾਵਰ) ਸਬੰਧਤ ਮੈਟ੍ਰਿਕਸ ਦਾ ਡਿਟ੍ਰੀਮੀਨੈਂਟ ਹੁੰਦਾ ਹੈ। ਜਿਵੇਂ ਉੱਪਰ ਦਰਸਾਏ 2 × 2 ਕੰਪਲੈਕਸ ਮੈਟ੍ਰਿਕਸ ਪ੍ਰਸਤੁਤੀ ਨਾਲ, ਗੁਣਾਂਕਾਂ ਦੀ ਅਨੁਕੂਲਤਾ ਮਜਬੂਰ ਕਰਕੇ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਨੂੰ ਦੁਬਾਰਾ ਪੈਦਾ ਰਚਿਆ ਜਾ ਸਕਦਾ ਹੈ; ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, ਜਿਵੇਂ c = d = 0 ਸੈੱਟ ਕਰਕੇ, ਦੋ 2 × 2 ਬਲੌਕਾਂ ਨਾਲ ਬਲੌਕ ਡਾਇਓਗਨਲ ਮੈਟ੍ਰਿਕਸ ਰਚੇ ਜਾਂਦੇ ਹਨ।
ਚਾਰ ਵਰਗਾਂ ਦਾ ਜੋੜ
[ਸੋਧੋ]ਨੰਬਰ ਥਿਊਰੀ ਵਿੱਚ, ਲਗਰਾਂਜ ਦੀ ਫੋਰ-ਸਕੁਏਅਰ ਥਿਊਰਮ (ਚਾਰ ਵਰਗ ਥਿਊਰਮ) ਦੇ ਸਬੂਤਾਂ ਵਿੱਚੋਂ ਇੱਕ ਸਬੂਤ ਦੇ ਤੌਰ ਤੇ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ ਵੀ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਜੋ ਦੱਸਦੀ ਹੈ ਕਿ ਹਰੇਕ ਗੈਰ-ਨੈਗੈਟਿਵ ਪੂਰਨ ਅੰਕ ਚਾਰ ਪੂਰਨ ਅੰਕ ਵਰਗਾਂ ਦਾ ਜੋੜ ਹੁੰਦਾ ਹੈ। ਅਪਣੇ ਆਪ ਵਿੱਚ ਇੱਕ ਸ਼ਾਨਦਾਰ ਥਿਊਰਮ ਹੋਣ ਦੇ ਨਾਤੇ, ਲਗਰਾਂਜ ਦੀ ਚਾਰ ਵਰਗ ਥਿਊਰਮ ਦੇ ਗਣਿਤ ਦੇ ਖੇਤਰਾਂ ਵਿੱਚ ਨੰਬਰ ਥਿਊਰੀ ਤੋਂ ਬਾਹਰ ਵੀ ਲਾਭਕਾਰੀ ਉਪਯੋਗ ਹਨ, ਜਿਵੇਂ ਕੰਬੀਨਾਟੋਰੀਅਲ ਡਿਜ਼ਾਈਨ ਥਿਊਰੀ। ਕੁਆਟ੍ਰਨੀਔਨ ਅਧਾਰਿਤ ਸਬੂਤ ਹੁਰਵਿਟਜ਼ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀ ਵਰਤੋ ਕਰਦਾ ਹੈ, ਜੋ ਸਾਰੇ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਰਿੰਗ ਦਾ ਇੱਕ ਸਬ-ਰਿੰਗ ਹੁੰਦਾ ਹੈ ਜਿਹਨਾਂ ਦੇ ਸਮਾਨ ਇੱਕ ਯੁਕਿਲਡਨ ਅਲੌਗਰਿਥਮ ਹੁੰਦਾ ਹੈ।
ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੇ ਜੋੜਿਆਂ ਦੇ ਰੂਪ ਵਿੱਚ ਕੁਆਟ੍ਰਨੀਔਨ
[ਸੋਧੋ]ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੇ ਜੋੜਿਆਂ ਦੇ ਰੂਪ ਵਿੱਚ ਪ੍ਰਸਤੁਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਇਸ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਤੋਂ, ਕੁਆਟ੍ਰਨੀਔਨ, ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਉੱਤੇ ਸੇਅਲੇਅ-ਡਿੱਕਸਨ ਬਣਤਰ ਲਾਗੂ ਕਰਨ ਦਾ ਨਤੀਜਾ ਹੁੰਦੇ ਹਨ। ਇਹ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੀ ਬਣਤਰ ਦਾ [[ਵਾਸਤਵਿਕ ਨੰਬਰ|ਵਾਸਤਵਿਕ ਨੰਬਰਾਂ}} ਦੇ ਜੋੜਿਆਂ ਦੇ ਰੂਪ ਵਿੱਚ ਸਰਵ ਸਧਾਰਨ ਕਰਨ ਹੈ।
ਮੰਨ ਲਓ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਉੱਤੇ ਕੋਈ ਦੋ-ਅਯਾਮੀ ਵੈਕਟਰ ਸਪੇਸ ਨੂੰ C2 ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਦੋ ਐਲੀਮੈਂਟਾਂ 1 ਅਤੇ j ਨਾਲ ਬਣਿਆ ਇੱਕ ਬੇਸਿਸ ਚੁਣੋ। ਬੇਸਿਸ ਐਲੀਮੈਂਟਾਂ 1 ਅਤੇ j ਦੇ ਸ਼ਬਦਾਂ ਵਿੱਚ C2 ਅੰਦਰ ਇੱਕ ਵੈਕਟਰ ਨੂੰ ਇਸ ਤਰਾਂ ਲਿਖਿਆ ਜਾ ਸਕਦਾ ਹੈ:
ਜੇਕਰ ਅਸੀਂ j2 = −1 ਅਤੇ ij = −ji ਪਰਿਭਾਸ਼ਿਤ ਕਰੀਏ, ਤਾਂ ਅਸੀਂ ਡਿਸਟ੍ਰੀਬਿਊਟਿਵ ਸਿਧਾਂਤ ਵਰਤਦੇ ਹੋਏ ਦੋ ਵੈਕਟਰਾਂ ਨੂੰ ਗੁਣਾ ਕਰ ਸਕਦੇ ਹਾਂ। ਗੁਣਨਫਲ ij ਦੀ ਜਗਹ k ਲਿਖਣਾ ਆਮ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਗੁਣਨਫਲ ਨਿਯਮਾਂ ਵਾਂਗ ਗੁਣਨਫਲ ਵੱਲ ਲਿਜਾਂਦਾ ਹੈ। ਇਸਲਈ, ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦਾ ਉੱਪਰ ਦਰਸਾਇਆ ਵੈਕਟਰ, ਕੁਆਟ੍ਰਨੀਔਨ a + bi + cj + dk ਨਾਲ ਸਬੰਧਤ ਹੈ। ਜੇਕਰ ਅਸੀਂ C2 ਦੇ ਐਲੀਮੈਂਟਾਂ ਨੂੰ ਵਿਵਸਥਿਤ ਜੋੜਿਆਂ ਦੇ ਰੂਪ ਵਿੱਚ ਲਿਖੀਏ ਅਤੇ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨੂੰ ਕੁਆਡ੍ਰਪਲਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਲਿਖੀਏ, ਤਾਂ ਇਹਨਾ ਦਰਮਿਆਨ ਸਬੰਧ ਇਹ ਬਣਦੇ ਹਨ;
−1 ਦਾ ਵਰਗਮੂਲ
[ਸੋਧੋ]ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਵਿੱਚ, ਸਿਰਫ ਦੋ ਨੰਬਰ ਹੁੰਦੇ ਹਨ, i ਅਤੇ –i, ਜਿਹਨਾਂ ਦਾ ਸਕੁਏਅਰ (ਵਰਗ) -1 ਹੁੰਦਾ ਹੈ। H ਵਿੱਚ ਮਾਇਨਸ ਇੱਕ ਦੇ ਅਨੰਤ ਤੌਰ ਤੇ ਬਹੁਤ ਸਾਰੇ ਵਰਗਮੂਲ ਹਨ: -1 ਦੇ ਵਰਗਮੂਲ ਲਈ ਕੁਆਟ੍ਰਨੀਔਨ ਹੱਲ R3 ਅੰਦਰ ਯੂਨਿਟ ਸਫੀਅਰ ਹੁੰਦਾ ਹੈ। ਇਸਨੂੰ ਦੇਖਣ ਲਈ, ਮੰਨ ਲਓ q = a + bi + cj + dk ਇੱਕ ਕੁਆਟ੍ਰਨੀਔਨ ਹੈ, ਅਤੇ ਮੰਨ ਲਓ ਕਿ ਇਸਦਾ ਵਰਗ -1 ਹੈ। a, b, c, ਅਤੇ d ਦੇ ਸ਼ਬਦਾਂ ਵਿੱਚ , ਇਸਦਾ ਅਰਥ ਹੈ ਕਿ
ਆਖਰੀ ਤਿੰਨ ਸਮੀਕਰਨਾਂ ਨੂੰ ਸੰਤੁਸ਼ਟ ਕਰਨ ਲਈ, ਜਾਂ ਤਾਂ a=0 ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਜਾਂ b,c ਅਤੇ d ਸਾਰੇ ਦੇ ਸਾਰੇ ਹੀ 0 ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ। ਬਾਦ ਵਾਲੀ ਸ਼ਰਤ ਅਸੰਭਵ ਹੈ ਕਿਉਂਕਿ a ਇੱਕ ਵਾਸਤਵਿਕ ਨੰਬਰ ਹੈ ਅਤੇ ਪਹਿਲੀ ਸਮੀਕਰਨ ਤੋਂ ਭਾਵ ਹੋਵੇਗਾ ਕਿ a2 = −1 ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ। ਇਸਲਈ a = 0 ਅਤੇ b2 + c2 + d2 = 1 ਹੀ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ। ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਇੱਕ ਕੁਆਟ੍ਰਨੀਔਨ ਦਾ ਵਰਗ -1 ਸਿਰਫ ਤੇ ਸਿਰਫ ਤਾਂ ਹੀ ਹੁੰਦਾ ਹੈ ਜੇਕਰ ਇਹ ਇੱਕ ਅਜਿਹਾ ਵੈਕਟਰ ਹੋਵੇ (ਯਾਨਿ ਕਿ ਸ਼ੁੱਧ ਕਾਲਪਨਿਕ ਹੋਵੇ) ਜਿਸਦਾ ਨੌਰਮ 1 ਹੋਵੇ। ਪਰਿਭਾਸ਼ਾ ਤੋਂ, ਸਾਰੇ ਅਜਿਹੇ ਵੈਕਟਰਾਂ ਦਾ ਸੈੱਟ ਯੂਨਿਟ ਸਫੀਅਰ ਰਚਦਾ ਹੈ।
ਸਿਰਫ ਨੈਗੈਟਿਵ ਵਾਸਤਵਿਕ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਹੀ ਵਰਗਮੂਲਾਂ ਦੀ ਅੰਨਤ ਸੰਖਿਆ ਹੁੰਦੀ ਹੈ। ਬਾਕੀ ਸਾਰਿਆਂ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਸਿਰਫ ਦੋ ਵਰਗਮੂਲ ਹੀ ਹੁੰਦੇ ਹਨ (ਜਾਂ 0 ਦੇ ਮਾਮਲੇ ਵਿੱਚ 1 ਹੁੰਦਾ ਹੈ)।
H ਵਿੱਚ ਮਾਈਨਸ ਇੱਕ ਦੇ ਵਰਗਮੂਲਾਂ ਦੀ ਪਛਾਣ ਹੈਮਿਲਟਨ ਦੁਆਰਾ ਦਿੱਤੀ ਗਈ ਸੀ, ਪਰ ਬਾਕੀ ਕਿਤਾਬਾਂ ਵਿੱਚ ਅਕਸਰ ਮਿਟਾ ਦਿੱਤੀ ਜਾਂਦੀ ਰਹੀ ਸੀ। 1971 ਵਿੱਚ ਸੈਮ ਪੈਰਲਿਸ ਦੁਆਰਾ ਹਿਸਟੋਰੀਕਲ ਟੌਪਿਕਸ ਇਨ ਅਲਜਬਰਾ (ਪੰਨਾ 39), ਜੋ ਨੈਸ਼ਨਲ ਕਾਉਂਸਲ ਔਫ ਟੀਚਰਜ਼ ਔਫ ਮੈਥੇਮੈਟਿਕਸ ਰਾਹੀਂ ਛਾਪੀ ਗਈ ਸੀ।, ਵਿੱਚ ਸਫੀਅਰ ਨੂੰ ਅਪਣੇ ਤਿੰਨ ਪੰਨਿਆਂ ਦੀ ਪ੍ਰਦ੍ਰਸ਼ਨੀ ਵਿੱਚ ਸ਼ਾਮਿਲ ਕੀਤਾ ਗਿਆ ਸੀ। ਤਾਜ਼ਾ ਸਮਿਆਂ ਵਿੱਚ, ਮਾਈਨਸ ਇੱਕ ਦੇ ਵਰਗ ਮੂਲਾਂ ਦੇ ਸਫੀਅਰ ਨੂੰ ਇਅਨ ਆਰ. ਪੋਰਟੇਇਓਸ ਦੀ ਕਿਤਾਬ ਕਲਿੱਫੋਰਡ ਅਲਜਬਰਾਜ਼ ਐਂਡ ਦੀ ਕਲਾਸੀਕਲ ਗਰੁੱਪਸ (ਕੈਂਬਰਿੱਜ, 1995) ਵਿੱਚ ਪੰਨਾ 60 ਉੱਤੇ ਕਥਨ 8.13 ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ। ਕੋਨਵੇਅ (2003) ਵਿੱਚ ਵੀ ਪੰਨਾ 40 ਉੱਤੇ ਕੁਆਟ੍ਰਨੀਔਨਜ਼ ਐਂਡ ਔਕਟੋਨੀਔਨਜ਼ ਵਿੱਚ ਅਸੀੰ ਪੜਦੇ ਹਾਂ: “ਕਿਸੇ ਵੀ ਕਾਲਪਨਿਕ ਯੂਨਿਟ ਨੂੰ i ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ, ਅਤੇ ਸਮਕੋਣ ਨੂੰ j , ਅਤੇ ਇਹਨਾਂ ਦੇ ਗੁਣਨਫਲ ਨੂੰ k ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ” , ਜੋ ਸਫੀਅਰ (ਗੋਲੇ) ਬਾਰੇ ਇੱਕ ਹੋਰ ਕਥਨ ਹੈ।
ਕੰਪਲੈਕਸ ਪਲੇਨਾਂ ਦੇ ਸੰਘ ਦੇ ਤੌਰ ਤੇ H
[ਸੋਧੋ]-1 ਦੇ ਵਰਗਮੂਲਾਂ ਦਾ ਹਰੇਕ ਜੋੜਾ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਅੰਦਰ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੀ ਇੱਕ ਵੱਖਰੀ ਨਕਲ ਪੈਦਾ ਕਰਦਾ ਹੈ, ਫੇਰ ਨਕਲ ਨੂੰ ਇਸ ਫੰਕਸ਼ਨ ਰਾਹੀਂ ਨਿਰਧਾਰਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ;
ਅਬਸਟ੍ਰੈਕਟ (ਅਮੂਰਤ) ਅਲਜਬਰੇ ਦੀ ਭਾਸ਼ਾ ਵਿੱਚ, ਹਰੇਕ ਹੀ, C ਤੋਂ H ਤੱਕ ਇੱਕ ਇੰਜੈਕਟਿਵ ਰਿੰਗ ਹੋਮੋਮੌਰਫਿਜ਼ਮ ਹੈ। ਜੜਾਂ (ਐਮਬੈੱਡਿੰਗਜ਼) ਦੀਆਂ ਤਸਵੀਰਾਂ ਜੋ q ਅਤੇ –q ਤੱਕ ਸਬੰਧਤ ਹੁੰਦੀਆਂ ਹਨ, ਇੱਕੋ ਜਿਹੀਆਂ ਹੁੰਦੀਆਂ ਹਨ।
ਹਰੇਕ ਗੈਰ-ਵਾਸਤਵਿਕ ਕੁਆਟ੍ਰਨੀਔਨ , H ਦੀ C ਪ੍ਰਤਿ ਇੱਕ ਆਇਸੋਮੌਰਫਿਕ ਸਬਸਪੇਸ ਵਿੱਚ ਰੱਖਿਆ ਹੁੰਦਾ ਹੈ। ਇਸਦੇ ਸਕੇਲਰ ਹਿੱਸੇ ਅਤੇ ਵੈਕਟਰ ਹਿੱਸੇ ਦੇ ਰੂਪ ਵਿੱਚ q ਨੂੰ ਇਸਤਰਾਂ ਲਿਖੋ:
ਵੈਕਟਰ ਹਿੱਸੇ ਨੂੰ ਹੋਰ ਅੱਗੇ ਇਸਦੇ ਨੌਰਮ ਅਤੇ ਇਸਦੇ ਵਰਸਰ ਦੇ ਰੂਪ ਵਿੱਚ ਤੋੜ ਕੇ ਲਿਖ ਦਿਓ:
(ਨੋਟ ਕਰੋ ਕਿ ਇਹ ਵਾਂਗ (ਬਰਾਬਰ) ਨਹੀਂ ਹੈ)। q ਦੇ ਵੈਕਟਰ ਹਿੱਸੇ ਦਾ ਵਰਸਰ , ਸ਼ੁੱਧ ਕਾਲਪਨਿਕ ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨ ਹੈ, ਇਸਲਈ ਇਸਦਾ ਵਰਗ -1 ਹੈ। ਇਸਤਰਾਂ, ਇਹ ਇਸ ਫੰਕਸ਼ਨ ਰਾਹੀਂ ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਦੀ ਇੱਕ ਨਕਲ ਨਿਰਧਾਰਿਤ ਕਰਦਾ ਹੈ।
ਇਸ ਫੰਕਸ਼ਨ ਅਧੀਨ, q , ਕੰਪਲੈਕਸ ਨੰਬਰ ਦੀ ਤਸਵੀਰ ਹੁੰਦਾ ਹੈ। ਇਸਤਰਾਂ, H, ਕਿਸੇ ਸਾਂਝੀ ਵਾਸਤਵਿਕ ਰੇਖਾ ਨੂੰ ਕੱਟਣ ਵਾਲੇ ਕੰਪਲੈਕਸ ਪਲੇਨਾਂ ਦਾ ਇੱਕ ਸੰਘ (ਯੂਨੀਅਨ) ਹੁੰਦਾ ਹੈ, ਜਿੱਥੇ ਯੂਨੀਅਨ ਨੂੰ ਮਾਈਨਸ ਇੱਕ ਦੇ ਵਰਗਮੂਲਾਂ ਵਾਲੇ ਸਫੀਅਰ ਉੱਤੇ ਮਨ ਵਿੱਚ ਇਹ ਰੱਖਦੇ ਹੋਏ ਲਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਇਹੀ ਪਲੇਨ (ਸਤਹਿ) ਸਫੀਅਰ ਦੇ ਐਂਟੌਪੋਡਲ (ਪ੍ਰਤਿਮੁੱਖ, ਉਲਟੇ ਪਾਸੇ) ਬਿੰਦੂਆਂ ਨਾਲ ਵੀ ਜੁੜਿਆ ਹੁੰਦਾ ਹੈ।
ਕਮਿਉਟੇਟਿਵ ਸਬ-ਰਿੰਗ
[ਸੋਧੋ]ਇੱਕ ਦੂਜੇ ਨਾਲ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਆਪਸੀ ਸਬੰਧ H ਦੇ ਕੰਪਲੈਕਸ ਸਬ-ਪਲੇਨਾਂ ਅੰਦਰ ਕਮਿਉਟੇਟਿਵ ਸਬ-ਰਿੰਗਾਂ ਦੇ ਸ਼ਬਦਾਂ ਵਿੱਚ ਵੀ ਪਛਾਣੇ ਅਤੇ ਲਿਖੇ ਜਾ ਸਕਦੇ ਹਨ। ਖਾਸ ਕਰ ਕੇ, ਕਿਉਂਕਿ ਦੋ ਕੁਆਟ੍ਰਨੀਔਨ p ਅਤੇ q ਸਿਰਫ ਤੇ ਸਿਰਫ ਤਾਂ ਹੀ ਕਮਿਊਟ (pq = qp) ਕਰਦੇ ਹਨ ਹਨ ਜੇਕਰ ਇਹ ਦੋਵੇਂ ਕੁਆਟ੍ਰਨੀਔਨ, H ਦੇ ਇੱਕੋ ਕੰਪਲੈਕਸ ਸਬ-ਪਲੇਨ ਅੰਦਰ ਰੱਖੇ ਹੋਏ ਹੋਣ, ਕੰਪਲੈਕਸ ਪਲੇਨਾਂ ਦੇ ਇੱਕ ਸੰਘ (ਯੂਨੀਅਨ) ਦੇ ਤੌਰ ਤੇ H ਦੀ ਰੂਪਰੇਖਾ (ਪ੍ਰੋਫਾਈਲ) ਉਦੋਂ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ਜਦੋਂ ਕੁਆਟ੍ਰਨੀਔਨ ਰਿੰਗ ਦੇ ਸਾਰੇ ਕਮਿਉਟੇਟਿਵ ਸਬ-ਰਿੰਗਾਂ ਨੂੰ ਖੋਜਣ ਦੀ ਇੱਛਾ ਪੈਦਾ ਹੁੰਦੀ ਹੈ। ਕਮਿਉਟੇਟਿਵ ਸਬ-ਰਿੰਗਾਂ ਵਾਲੀ ਇਹ ਵਿਧੀ ਸਹੋਯੋਗੀ-ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਅਤੇ 2×2 ਵਾਸਤਵਿਕ ਮੈਟ੍ਰਿਕਸਾਂ ਦੀ ਪ੍ਰੋਫਾਈਲ (ਰੂਪਰੇਖਾ) ਬਣਾਉਣ ਲਈ ਵਰਤੀ ਜਾਂਦੀ ਹੈ।
ਇੱਕ ਕੁਆਟ੍ਰਨੀਔਨ ਅਸਥਿਰਾਂਕ ਦੇ ਫੰਕਸ਼ਨ
[ਸੋਧੋ]ਕਿਸੇ ਕੰਪਲੈਕਸ ਅਸਥਿਰਾਂਕ ਦੇ ਫੰਕਸ਼ਨਾਂ ਵਾਂਗ, ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਅਸਥਿਰਾਂਕ ਦੇ ਫੰਕਸ਼ਨ ਵੀ ਵਰਤੋ ਵਿੱਚ ਆਉਣ ਵਾਲੇ ਭੌਤਿਕੀ ਮੌਡਲ ਸੁਝਾਉਂਦੇ ਹਨ। ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, "ਮੈਕਸਵੈੱਲ"ਦੁਆਰਾ ਦਰਸਾਈਆਂ ਮੂਲ ਇਲੈਕਟ੍ਰਿਕ ਅਤੇ ਮੈਗਨੈਟਿਕ ਫੀਲਡਾਂ ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਅਸਥਿਰਾਂਕ ਦੇ ਫੰਕਸ਼ਨ ਸਨ।
ਐਕਸਪੋਨੈਂਸ਼ੀਅਲ, ਲੌਗਰਿਥਮ, ਅਤੇ ਪਾਵਰ
[ਸੋਧੋ]ਕਿਸੇ ਦਿੱਤੇ ਹੋਣ ਕੁਆਟ੍ਰਨੀਔਨ,
ਲਈ ਐਕਪੋਨੈਂਸ਼ੀਅਲ ਨੂੰ ਇਸਤਰਾਂ ਗਿਣਿਆ ਜਾਂਦਾ ਹੈ
ਅਤੇ
- .[2]
ਇਸਤੋਂ ਇਹ ਪਤਾ ਚਲਦਾ ਹੈ ਕਿ ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਦੀ ਪੋਲਰ ਡਿਕੰਪੋਜ਼ੀਸ਼ਨ ਨੂੰ ਇਸਤਰਾਂ ਲਿਖਿਆ ਜਾ ਸਕਦਾ ਹੈ;
ਜਿੱਥੇ ਐਂਗਲ ਅਤੇ ਯੂਨਿਟ ਵੈਕਟਰ ਇਸਤਰਾਂ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ:
ਅਤੇ
ਕੋਈ ਵੀ ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨ ਪੋਲਰ ਰੂਪ ਵਿੱਚ ਲਿਖ ਕੇ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ।
ਕਿਸੇ ਕੁਆਟ੍ਰਨੀਔਨ ਦੀ ਪਾਵਰ ਨੂੰ ਕਿਸੇ ਮਨਚਾਹੇ (ਵਾਸਤਵਿਕ) ਐਕਸਪੋਨੈਂਟ ਤੱਕ ਇਸ ਤਰਾਂ ਚੁੱਕਿਆ ਜਾ ਸਕਦਾ ਹੈ:
ਤਿੰਨ ਅਯਾਮੀ ਅਤੇ ਚਾਰ ਅਯਾਮੀ ਰੋਟੇਸ਼ਨਲ ਗਰੁੱਪ
[ਸੋਧੋ]ਉੱਪਰ ਦਿੱਤੇ ਅਰਥਾਂ ਦੇ ਬਾਵਜੂਦ, ਸ਼ਬਦ “ਕੰਜੂਗੇਸ਼ਨ” ਦਾ ਇੱਕ ਅਰਥ ਇਹ ਵੀ ਹੈ ਕਿ ਕਿਸੇ ਐਲੀਮੈਂਟ ਨੂੰ a ਤੋਂ rar−1 ਤੱਕ ਲੈਣਾ ਜਿੱਥੇ r ਕੋਈ ਗੈਰ-ਜ਼ੀਰੋ ਐਲੀਮੈਂਟ (ਕੁਆਟ੍ਰਨੀਔਨ) ਹੈ। ਉਹ ਸਾਰੇ ਐਲੀਮੈਂਟ ਜੋ ਕਿਸੇ ਦਿੱਤੇ ਹੋਏ ਐਲੀਮੈਂਟ ਪ੍ਰਤਿ ਕੰਜੂਗੇਟ ਹੋਣ (ਸ਼ਬਦ ਕੰਜੂਗੇਟ ਦੀ ਸਮਝ ਮੁਤਾਬਕ), ਉਹ ਵੈਕਟਰ ਹਿੱਸੇ ਦਾ ਉਹੀ ਨੌਰਮ ਅਤੇ ਇੱਕੋ ਵਾਸਤਵਿਕ ਹਿੱਸਾ ਰੱਖਦੇ ਹੋਣਗੇ। (ਇਸਤਰਾਂ ਕੰਜੂਗੇਟ ਦਾ ਦੂਜਾ ਅਰਥ ਕੰਜੂਗੇਟਾਂ ਵਿੱਚੋਂ ਇੱਕ ਕੰਜੂਗੇਟ ਹੋਣਾ ਹੈ)
ਇਸਤਰਾਂ, ਗੈਰ-ਜ਼ੀਰੋ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦਾ ਗੁਣਾ ਕਰਨ ਵਾਲਾ ਗਰੁੱਪ, ਜ਼ੀਰੋ ਦੇ ਬਰਾਬਰ ਵਾਸਤਵਿਕ ਹਿੱਸੇ ਵਾਲੇ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨਾਲ ਬਣੀ R3 ਦੀ ਨਕਲ ਉੱਤੇ ਕੰਜੂਗੇਸ਼ਨ ਰਾਹੀਂ ਕ੍ਰਿਆ ਕਰਦਾ ਹੈ। ਕਿਸੇ ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨ (ਸ਼ੁਧ 1 ਮੁੱਲ ਵਾਲੇ ਇੱਕ ਕੁਆਟ੍ਰਨੀਔਨ) ਜਿਸਦਾ ਵਾਸਤਵਿਕ ਹਿੱਸਾ cos(θ) ਹੋਵੇ, ਰਾਹੀਂ ਕੰਜੂਗੇਸ਼ਨ ਦਾ ਅਰਥ ਹੈ ਇੱਕ ਐਂਗਲ 2θ ਰਾਹੀਂ ਰੋਟੇਸ਼ਨ, ਜਿਸ ਵਿੱਚ ਰੋਟੇਸ਼ਨ ਦਾ ਐਕਸਿਸ ਕਾਲਪਨਿਕ ਹਿੱਸੇ ਦੀ ਦਿਸ਼ਾ ਹੁੰਦੀ ਹੈ। ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੇ ਇਹ ਫਾਇਦੇ ਹਨ:
- ਗੈਰ-ਸਿੰਗੁਲਰ ਪ੍ਰਸਤੁਤੀ (ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, ਇਲੁਰ ਐਂਗਲਾਂ ਨਾਲ ਤੁਲਨਾ ਦੇ ਤੌਰ ਤੇ)
- ਮੈਟ੍ਰਿਕਸਾਂ ਨਾਲੋਂ ਜਿਆਦਾ ਸੰਖੇਪ (ਅਤੇ ਤੇਜ਼)।
- ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨ ਦੇ ਜੋੜੇ 4D ਸਪੇਸ ਵਿੱਚ ਇੱਕ ਰੋਟੇਸ਼ਨ ਪ੍ਰਸਤੁਤ ਕਰਦੇ ਹਨ (ਦੇਖੋ 4-ਡਾਇਮੈਨਸ਼ਨਲ ਯੁਕਿਲਡਨ ਸਪੇਸ ਵਿੱਚ ਰੋਟੇਸ਼ਨਾਂ: 4D ਰੋਟੇਸ਼ਨਾਂ ਦਾ ਅਲਜਬਰਾ)।
ਸਾਰੇ ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨਾਂ (ਵਰਸਰਾਂ) ਦਾ ਸੈੱਟ, ਗੁਣਾ ਕਰਨ ਤੇ, ਇੱਕ 3-ਸਫੀਅਰ S3 ਅਤੇ ਇੱਕ ਗਰੁੱਪ (ਇੱਕ ਲਾਈ ਗਰੁੱਪ) ਰਚਦਾ ਹੈ, ਜਿਸ ਵਿੱਚ ਇਹ ਡਿਟ੍ਰਮੀਨੈਂਟ 1 ਵਾਲੇ ਵਾਸਤਵਿਕ ਔਰਥੋਗਨਲ 3×3 ਮੈਟ੍ਰਿਕਸਾਂ ਦੇ ਗਰੁੱਪ SO(3, R) ਨੂੰ ਦੋ ਵਾਰ ਕਵਰ ਕਰਦਾ ਹੈ ਕਿਉਂਕਿ ਦੋ ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨ ਉੱਪਰ ਦੱਸੀ ਆਪਸੀ ਸਬੰਧ ਵਿਸ਼ੇਸ਼ਤਾ ਅਧੀਨ ਹਰੇਕ ਰੋਟੇਸ਼ਨ ਨਾਲ ਸਬੰਧ ਰੱਖਦੇ ਹਨ।
ਇਸ ਵਿਸ਼ੇ ਤੇ ਹੋਰ ਵਿਸਥਾਰਪੂਰਵਕ ਜਾਣਕਾਰੀ ਲਈ ਦੇਖੋ : ਤਿੰਨ ਅਯਾਮਾਂ ਵਿੱਚ ਬਿੰਦੂ ਗਰੁੱਪ।
ਵਰਸਰਾਂ ਦੇ ਕਿਸੇ ਸਬ-ਗਰੁੱਪ ਦੀ ਤਸਵੀਰ ਇੱਕ ਬਿੰਦੂ ਗਰੁੱਪ ਹੁੰਦੀ ਹੈ, ਅਤੇ ਇਸਤੋਂ ਉਲਟ ਤਰੀਕੇ ਨਾਲ, ਕਿਸੇ ਬਿੰਦੂ ਗਰੁੱਪ ਦੀ ਮੁਢਲੀ ਤਸਵੀਰ ਵਰਸਰਾਂ ਦਾ ਇੱਕ ਸਬ-ਗਰੁੱਪ ਹੁੰਦੀ ਹੈ। ਕਿਸੇ ਸੀਮਤ ਬਿੰਦੂ ਗਰੁੱਪ ਦੀ ਮੂਲ ਤਸਵੀਰ ਨੂੰ ਅੱਗੇ ਬਾਇਨਰੀ ਲਿਖ ਕੇ ਉਸੇ ਨਾਮ ਨਾਲ ਬੁਲਾਇਆ ਜਾਂਦਾ ਹੈ। ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ, ਇਕੋਸਾਹੀਡਰਲ ਗਰੁੱਪ ਦੀ ਮੂਲ ਤਸਵੀਰ "ਬਾਇਨਰੀ ਇਕੋਸਾਹੀਡਰਲ ਗਰੁੱਪ" ਹੁੰਦੀ ਹੈ।
ਵਰਸਰਾਂ ਦਾ ਗਰੁੱਪ, ਡਿਟ੍ਰੀਮੀਨੈਂਟ 1 ਵਾਲੇ ਕੰਪਲੈਕਸ ਯੂਨਾਇਟਰੀ 2×2 ਮੈਟ੍ਰਿਕਸਾਂ ਦੇ ਗਰੁੱਪ SU(2) ਪ੍ਰਤਿ ਆਇਸੋਮੌਰਫਿਕ ਹੁੰਦਾ ਹੈ।
ਮੰਨ ਲਓ A ਕੋਈ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦਾ ਸੈੱਟ ਹੈ ਜੋ a + bi + cj + dk ਰੂਪ ਵਾਲੇ ਹਨ ਜਿੱਥੇ a, b, c, ਅਤੇ d ਜਾਂ ਤਾਂ ਸਾਰੇ ਦੇ ਸਾਰੇ ਹੀ ਪੂਰਨ ਅੰਕ ਹਨ ਜਾਂ ਰੇਸ਼ਨਲ ਨੰਬਰ ਹਨ ਜਿਹਨਾਂ ਦਾ ਨਿਊਮਰੇਟਰ ਔਡ ਅਤੇ ਡੀਨੋਮੀਨੇਟਰ 2 ਹੈ। ਸੈੱਟ A ਇੱਕ ਰਿੰਗ (ਅਸਲ ਵਿੱਚ ਇੱਕ ਡੋਮੇਨ) ਹੁੰਦਾ ਹੈ ਅਤੇ ਇੱਕ ਲੈੱਟਿਸ ਹੁੰਦਾ ਹੈ, ਜਿਸਨੂੰ ਹੁਰਵਿਟਜ਼ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦਾ ਰਿੰਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇਸ ਰਿੰਗ ਵਿੱਚ 24 ਯੂਨਿਟ ਕੁਆਟ੍ਰਨੀਔਨ ਹੁੰਦੇ ਹਨ, ਅਤੇ ਇਹ ਸ਼ਲਾਫਲੀ ਚਿੰਨ {3,4,3} ਵਾਲੇ ਇੱਕ 24-ਸੈੱਲਾਂ ਦੇ ਨਿਯਮਿਤ (ਰੈਗੂਲਰ) ਪੌਲੀਟੋਪ ਦੇ ਸ਼ਿਖਰ (ਵਰਟੀਸਿਜ਼) ਹੁੰਦੇ ਹਨ।
ਸਰਵ ਸਧਾਰਨਕਰਨ
[ਸੋਧੋ]ਜੇਕਰ F ਕੋਈ ਅਜਿਹੀ ਫੀਲਡ ਹੋਵੇ ਜਿਸਦੀ ਵਿਸ਼ੇਸ਼ਤਾ 2 ਤੋਂ ਵੱਖਰੀ ਹੋਵੇ, ਅਤੇ a ਅਤੇ b ਇਸਦੇ ਐਲੀਮੈਂਟ ਹੋਣ, ਤਾਂ F ਉੱਪਰ ਇੱਕ ਅਜਿਹਾ ਚਾਰ-ਅਯਾਮੀ ਯੂਨਾਇਟਰੀ ਐਸੋਸੀਏਟਿਵ ਅਲਜਬਰਾ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਜਿਸਦੇ ਬੇਸਿਸ 1, i, j, ਅਤੇ ij ਹੋਣ, ਜਿੱਥੇ i2 = a, j2 = b ਅਤੇ ij = −ji (ਤਾਂ ਜੋ (ij)2 = −ab) ਹੋਵੇ। ਇਹਨਾਂ ਅਲਜਬਰਿਆਂ ਨੂੰ ਕੁਆਟ੍ਰਨੀਔਨ ਅਲਜਬਰੇ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਹ F ਉੱਤੇ ਡਿਵੀਜ਼ਨ ਅਲਜਬਰੇ ਰਚਣ ਲਈ, a ਅਤੇ b ਦੀ ਚੋਣ ਤੇ ਨਿਰਭਰ ਕਰਦੇ ਹੋਏ, F ਉੱਤੇ 2×2 ਮੈਟ੍ਰਿਕਸਾਂ ਦੇ ਅਲਜਬਰੇ ਪ੍ਰਤਿ ਆਇਸੋਮਰਫਿਕ ਹੁੰਦੇ ਹਨ।
Cℓ3,0(R) ਦੇ ਇਵਨ ਹਿੱਸੇ ਦੇ ਤੌਰ ਤੇ ਕੁਆਟ੍ਰਨੀਔਨ
[ਸੋਧੋ]ਰੇਖਾਗਣਿਤਕ ਹਿਸਾਬਾਂ ਕਿਤਾਬਾਂ ਲਈ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀ ਲਾਭਕਾਰੀ ਵਰਤੋਂ ਦਾ ਕਲਿੱਫੋਰਡ ਅਲਜਬਰਾ Cℓ3,0(R) ਦੇ ਇਵਨ ਹਿੱਸੇ Cℓ+3,0(R) ਦੇ ਰੂਪ ਵਿੱਚ ਪਛਾਣਨ ਰਾਹੀਂ, ਹੋਰ ਅਯਾਮਾਂ ਤੱਕ ਸਰਵ ਸਧਾਰਨਕਰਨ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਇਹ ਮੁਢਲੇ ਬੇਸਿਸ ਐਲੀਮੈਂਟਾਂ σ1, σ2, σ3 ਤੋਂ ਗੁਣਨਫਲ ਨਿਯਮਾਂ ਨੂੰ ਵਰਤ ਕੇ ਬਣਿਆ ਇੱਕ ਐਸੋਸੀਏਟਿਵ ਮਲਟੀਵੈਕਟਰ ਅਲਜਬਰਾ ਹੁੰਦਾ ਹੈ;
ਜੇਕਰ ਇਹ ਮੁਢਲੇ ਬੇਸਿਸ ਐਲੀਮੈਂਟ 3D ਸਪੇਸ ਵਿੱਚ ਵੈਕਟਰਾਂ ਨੂੰ ਪ੍ਰਸਤੁਤ ਕਰਨ ਲਈ ਲਏ ਜਾਣ, ਤਾਂ ਇਹ ਨਤੀਜਾ ਨਿਕਲਦਾ ਹੈ ਕਿ ਕਿਸੇ ਯੂਨਿਟ ਵੈਕਟਰ w ਤੋਂ ਸਮਕੋਣ ਤੇ ਕਿਸੇ ਪਲੇਨ ਵਿੱਚ ਕਿਸੇ ਵੈਕਟਰ r ਦਾ ਪਰਛਾਵਾਂ (ਰਿੱਫਲੈਕਸ਼ਨ) ਇਸਤਰਾਂ ਲਿਖਿਆ ਜਾ ਸਕਦਾ ਹੈ:
ਦੋ ਰਿੱਫਲੈਕਸ਼ਨਾਂ, ਦੋਵੇਂ ਰਿੱਫਲੈਕਸ਼ਨ ਪਲੇਨਾਂ ਦਰਮਿਆਨ ਐਂਗਲ ਤੋਂ ਦੁੱਗਣੇ ਐਂਗਲ ਰਾਹੀਂ ਇੱਕ ਰੋਟੇਸ਼ਨ ਬਣਾਉਂਦੀਆਂ ਹਨ। ਇਸਲਈ ,
ਓਸ ਪਲੇਨ ਵਿੱਚ ਇੱਕ 180° ਦੀ ਰੋਟੇਸ਼ਨ ਨਾਲ ਸਬੰਧਤ ਹੁੰਦੀਆਂ ਹਨ ਜਿਸ ਪਲੇਨ ਵਿੱਚ σ1 ਅਤੇ σ2 ਰੱਖੇ ਹੁੰਦੇ ਹਨ। ਇਹ ਇਸ ਸਬੰਧਤ ਕੁਆਟ੍ਰਨੀਔਨ ਫਾਰਮੂਲੇ ਨਾਲ ਬਹੁਤ ਜਿਆਦਾ ਮਿਲਦੀ ਜੁਲਦੀ ਚੀਜ਼ ਹੈ,
ਅਸਲ ਵਿੱਚ, ਇਹ ਦੋਵੇਂ ਇੱਕੋ ਚੀਜ਼ ਹਨ, ਜੇਕਰ ਅਸੀਂ ਪਛਾਣ ਕਰਦੇ ਹਾਂ
ਅਤੇ ਇਹ ਸਿੱਧਾ ਹੀ ਸਾਬਤ ਹੋ ਜਾਂਦਾ ਹੈ ਕਿ ਇਹ ਇਹਨਾਂ ਹੈਮਿਲਟਨ ਸਬੰਧਾਂ ਨੂੰ ਸੁਰੱਖਿਅਤ ਕਰਦਾ ਹੈ,
ਇਸ ਤਸਵੀਰ ਵਿੱਚ, ਕੁਆਟ੍ਰਨੀਔਨ ਵੈਕਟਰਾਂ ਨਾਲ ਸਬੰਧਤ ਨਹੀਂ ਹੁੰਦੇ ਸਗੋਂ ਬਾਇਵੈਕਟਰਾਂ ਨਾਲ ਸਬੰਧਤ ਹੁੰਦੇ ਹਨ- ਜੋ ਅਜਿਹਆਂ ਮਾਤਰਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਹਨਾਂ ਦਾ ਮੁੱਲ ਅਤੇ ਦਿਸ਼ਾਵਾਂ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ 2D ਪਲੇਨਾਂ ਨਾਲ ਸਬੰਧਿਤ ਹੁੰਦਾ ਹੈ ਨਾ ਕਿ 1D ਦਿਸ਼ਾਵਾਂ ਨਾਲ। ਕੰਪਲੈਕਸ ਨੰਬਰਾਂ ਨਾਲ 2D ਵਿੱਚ ਵੀ ਸਬੰਧ ਸਪਸ਼ਟ ਹੋ ਜਾਂਦੇ ਹਨ, ਜਿਸ ਵਿੱਚ ਦੋ ਵੈਕਟਰ ਦਿਸ਼ਾਵਾਂ σ1 ਅਤੇ σ2 ਹੁੰਦੀਆਂ ਹਨ, ਸਿਰਫ ਇੱਕ ਬਾਇਵੈਕਟਰ ਬੇਸਿਸ ਐਲੀਮੈਂਟ σ1σ2 ਹੁੰਦਾ ਹੈ, ਇਸਲਈ ਸਿਰਫ ਇੱਕ ਹੀ ਕਾਲਪਨਿਕ ਹੁੰਦਾ ਹੈ। ਪਰ, ਤਿੰਨ ਵੈਕਟਰ ਦਿਸ਼ਾਵਾਂ ਵਾਲੀ 3D ਵਿੱਚ, ਤਿੰਨ ਬਾਇਵੈਕਟਰ ਬੇਸਿਸ ਐਲੀਮੈਂਟ σ1σ2, σ2σ3, σ3σ1 ਹੁੰਦੇ ਹਨ , ਇਸਲਈ ਤਿੰਨ ਕਾਲਪਨਿਕ ਹੁੰਦੇ ਹਨ।
ਕਾਰਣ ਹੋਰ ਅੱਗੇ ਤੱਕ ਜਾਂਦੇ ਹਨ। ਕਲਿੱਫੋਰਡ ਅਲਜਬਰੇ Cℓ4,0(R) ਵਿੱਚ, ਛੇ ਬਾਇਵੈਕਟਰ ਬੇਸਿਸ ਐਲੀਮੈਂਟ ਹੁੰਦੇ ਹਨ, ਕਿਉਂਕਿ ਚਾਰ ਵੱਖਰੀਆਂ ਬੇਸਿਸ ਵੈਕਟਰ ਦਿਸ਼ਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ। ਛੇ ਵੱਖਰੇ ਜੋੜੇ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇਸ ਕਰਕੇ ਛੇ ਹੀ ਵੱਖਰੇ ਰੇਖਿਕ ਤੌਰ ਤੇ ਸੁਤੰਤਰ ਪਲੇਨਾਂ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀਆਂ ਇਹਨਾਂ ਜਨਰਲਾਇਜ਼ੇਸ਼ਨਾਂ ਨੂੰ ਵਰਤਦੇ ਹੋਏ ਅਜਿਹੀਆਂ ਸਪੇਸਾਂ ਅੰਦਰ ਰੋਟੇਸ਼ਨਾਂ, ਜਿਹਨਾਂ ਨੂੰ ਰੋਟਰ (ਬਹੁਵਚਨ ਰੋਟਰਜ਼) ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਹੋਮੋਜੀਨੀਅਸ ਕੋਆਰਡੀਨੇਟਾਂ (ਇੱਕਸਾਰ ਨਿਰਦੇਸ਼ਾਂਕਾਂ) ਵਾਲੇ ਉਪਯੋਗਾਂ ਲਈ ਬਹੁਤ ਲਾਭਕਾਰੀ ਹੋ ਸਕਦੀਆਂ ਹਨ। ਪਰ ਸਿਰਫ 3D ਵਿੱਚ ਹੀ ਬੇਸਿਸ ਬਾਇਵੈਕਟਰਾਂ ਦੀ ਇਹ ਸੰਖਿਆ ਬੇਸਿਸ ਵੈਕਟਰਾਂ ਦੀ ਗਿਣਤੀ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ, ਅਤੇ ਹਰੇਕ ਬਾਇਵੈਕਟਰ ਨੂੰ ਇੱਕ "ਸੂਡੋਵੈਕਟਰ" ਦੇ ਰੂਪ ਵਿੱਚ ਪਛਾਣਿਆ ਜਾ ਸਕਦਾ ਹੈ।
ਹੋਰ ਜਿਗਿਆਸਾ ਦੇ ਲਈ, ਇਸ ਸੈੱਟਿੰਗ ਵਿੱਚ ਕੁਆਟ੍ਰਨੀਔਨ ਨੂੰ ਸਥਾਨਬੱਧ ਕਰਕੇ ਹੇਠਾਂ ਲਿਖੇ ਲਾਭਾਂ ਨੂੰ ਪਛਾਣੋ:
- ਰੇਖਾਗਣਿਤਿਕ ਅਲਜਬਰੇ ਅੰਦਰ ਰੋਟਰਜ਼ ਕੁਦਰਤੀ ਅਤੇ ਗੈਰ-ਰਹੱਸਮਈ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇੱਕ ਦੋਹਰੀ ਰਿੱਫਲੈਕਸ਼ਨ ਦੀ ਸੰਕੇਤ-ਬੱਧਤਾ (ਐੱਨਕੋਡਿੰਗ) ਦੇ ਰੂਪ ਵਿੱਚ ਅਸਾਨੀ ਨਾਲ ਸਮਝਣਯੋਗ ਹੁੰਦੇ ਹਨ।
- ਰੇਖਾਗਣਿਤਿਕ ਅਲਜਬਰੇ ਅੰਦਰ, ਇੱਕ ਰੋਟਰ ਅਤੇ ਜਿਸ ਵਸਤੂ ਤੇ ਇਹ ਕ੍ਰਿਆ ਕਰਦਾ ਹੈ, ਉਹ ਵਸਤੂ, ਇੱਕੋ ਜਗਹ ਰਹਿੰਦੇ ਹਨ। ਇਹ ਪ੍ਰਸਤੁਤੀਆਂ ਬਦਲਣ ਦੀ ਜਰੂਰਤ ਅਤੇ ਨਵੀਆਂ ਆਂਕੜਾ ਬਣਤਰਾਂ ਅਤੇ ਵਿਧੀਆਂ ਨੂੰ ਚਿੰਨਬੱਧ ਕਰਨ (ਐੱਨਕੋਡ ਕਰਨ) ਦੀ ਜਰੂਰਤ ਨੂੰ ਖਤਮ ਕਰ ਦਿੰਦਾ ਹੈ (ਜਿਸਦੀ ਉਦੋਂ ਜਰੂਰਤ ਪੈਂਦੀ ਹੈ ਜਦੋਂ ਰੇਖਿਕ ਅਲਜਬਰੇ ਨੂੰ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਨਾਲ ਵਧਾਉਣਾ ਹੁੰਦਾ ਹੈ)।
- ਅਲਜਬਰੇ ਦੇ ਕਿਸੇ ਵੀ ਐਲੀਮੈਂਟ ਉੱਤੇ ਇੱਕ ਰੋਟਰ ਨੂੰ ਬ੍ਰਹਿਮੰਡੀ ਤੌਰ ਤੇ ਲਾਗੂ ਕੀਤਾ ਸਕਦਾ ਹੈ, ਸਿਰਫ ਵੈਕਟਰਾਂ ਅਤੇ ਹੋਰ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਉੱਤੇ ਹੀ ਨਹੀਂ, ਸਗੋਂ ਰੇਖਾਵਾਂ, ਸਤਹਿਾਂ (ਪਲੇਨਾਂ), ਚੱਕਰਾਂ, ਸਫੀਅਰਾਂ (ਗੋਲਿਆਂ), ਕਿਰਨਾਂ (ਰੇਅਜ਼), ਅਤੇ ਹੋਰ ਬਹੁਤ ਕੁੱਝ ਇਸੇ ਤਰਾਂ ਦੀਆਂ ਚੀਜ਼ਾਂ ਤੇ ਵੀ ਲਾਗੂ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ।
- ਯੁਕਿਲਡਨ ਜੀਓਮੈਟਰੀ ਦੇ ਕਨਫਰਮਲ ਮਾਡਲ ਵਿੱਚ, ਰੋਟਰਜ਼, ਅਲਜਬਰੇ ਦੇ ਕਿਸੇ ਸਿੰਗਲ ਐਲੀਮੈਂਟ ਉੱਤੇ ਕ੍ਰਿਆ ਕਰਕੇ ਉਸ ਵਿੱਚ ਰੋਟੇਸ਼ਨਾਂ, ਪਰਿਵਰਤਨਾਂ ਅਤੇ ਸਕੇਲਿੰਗ ਦੀ ਐੱਨਕੋਡਿੰਗ ਦੀ ਆਗਿਆ ਦਿੰਦੇ ਹਨ। ਖਾਸ ਕਰਕੇ, ਇਸਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਰੋਟਰਜ਼ ਕਿਸੇ ਮਨਚਾਹੇ ਧੁਰੇ ਦੁਆਲੇ ਰੋਟੇਸ਼ਨਾਂ ਨੂੰ ਪ੍ਰਸਤੁਤ ਕਰ ਸਕਦੇ ਹਨ, ਜਦੋਂਕਿ ਕੁਆਟ੍ਰਨੀਔਨ ਉਰਿਜਨ ਰਾਹੀਂ ਹੁੰਦੇ ਹੋਏ ਕਿਸੇ ਧੁਰੇ ਤੱਕ ਸੀਮਤ ਹੁੰਦੇ ਹਨ।
- ਰੋਟਰ-ਐੱਨਕੋਡਿਡ ਟਰਾਂਸਫੋਰਮੇਸ਼ਨਾਂ (ਪਰਿਵਰਤਨ) ਵਿਸ਼ੇਸ ਤੌਰ ਤੇ ਸਿੱਧੇ ਰੂਪ ਵਿੱਚ ਇੰਟਰਪੋਲੇਸ਼ਨ (ਅੰਤਰ-ਧਰੁਵ) ਬਣਾਉਂਦੀਆਂ ਹਨ।
ਕਲਿੱਫੋਰਡ ਅਲਜਬਰਿਆਂ ਦੀਆਂ ਰੇਖਾਗਣਿਤਿਕ ਵਰਤੋਆਂ ਬਾਰੇ ਹੋਰ ਵਿਸਥਾਰਪੂਰਵਕ ਜਾਣਕਾਰੀ ਲਈ, ਦੇਖੋ "ਰੇਖਾਗਣਿਤਿਕ ਅਲਜਬਰਾ"
ਬਰਾਓਇਰ ਗਰੁੱਪ
[ਸੋਧੋ]ਕੁਆਟ੍ਰਨੀਔਨ, ਵਾਸਤਵਿਕ ਨੰਬਰਾਂ ਉੱਤੇ ਜਰੂਰ ਹੀ ਇਕਲੌਤੇ (ਗੈਰ-ਸੂਖਮ) ਕੇਂਦਰੀ ਸਰਲ ਅਲਜਬਰਾ (ਸੈਂਟਰਲ ਸਿੰਪਲ ਅਲਜਬਰਾ) (CSA) ਹਨ ਕਿਉਂਕਿ ਵਾਸਤਵਿਕਾਂ ਉੱਪਰ ਹਰੇਕ CSA, ਜਾਂ ਤਾਂ ਵਾਸਤਵਿਕਾਂ ਬਰਾਬਰ ਜਾਂ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਬਰਾਬਰ ਇੱਕ ਬਰਾਓਇਰ ਹੁੰਦਾ ਹੈ। ਸਪਸ਼ਟ ਰੂਪ ਵਿੱਚ, ਵਾਸਤਵਿਕਾਂ ਦਾ ਬਰਾਓਇਰ ਗਰੁੱਪ ਦੋ ਸ਼੍ਰੇਣੀਆਂ ਨਾਲ ਬਣਿਆ ਹੁੰਦਾ ਹੈ, ਜਿਹਨਾਂ ਨੂੰ ਵਾਸਤਵਿਕਾਂ ਅਤੇ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਰਾਹੀਂ ਪ੍ਰਸਤੁਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਜਿੱਥੇ ਬਰਾਓਇਰ ਗਰੁੱਪ ਸਾਰੇ CSAਆਂ ਦਾ, ਇੱਕ ਮੈਟ੍ਰਿਕਸ ਰਿੰਗ ਰੂਪੀ CSA ਦੇ ਇੱਕ ਹੋਰ ਉੱਤੇ ਬਰਾਬਰਤਾ ਦੇ ਸਬੰਧ ਤੱਕ ਦਾ ਸੈੱਟ ਹੁੰਦਾ ਹੈ। ਅਰਟਿਨ-ਵੈੱਡਰਬਰਨ ਥਿਊਰਮ (ਵਿਸ਼ੇਸ਼ ਤੌਰ ਤੇ, ਵੈੱਡਰਬਰਨ ਹਿੱਸਾ) ਮੁਤਾਬਿਕ, CSAਆਂ ਦੇ, ਕਿਸੇ ਡਿਵੀਜ਼ਨ ਅਲਜਬਰੇ ਉੱਤੇ ਸਾਰੇ ਮੈਟ੍ਰਿਕਸ ਅਲਜਬਰੇ, ਅਤੇ ਇਸਤਰਾਂ ਕੁਆਟ੍ਰਨੀਔਨ ਵਾਸਤਵਿਕ ਅੰਕਾਂ ਉੱਤੇ ਇਕਲੌਤੇ ਗੈਰ-ਸੂਖਮ ਡਿਵੀਜ਼ਨ ਅਲਜਬਰੇ ਹਨ।
ਕਿਸੇ ਫੀਲਡ ਉੱਤੇ CSAਆਂ ਦੇ ਰਿੰਗ, ਜੋ ਅਜਿਹੇ ਸਰਲ ਅਲਜਬਰੇ ਹੁੰਦੇ ਹਨ (ਜਿਹਨਾਂ ਦੇ ਕੋਈ ਵੀ ਗੈਰ-ਸੂਖਮ 2 ਪਾਸੇ ਆਦਰਸ਼ ਨਹੀਂ ਹੁੰਦੇ, ਜਿਵੇਂ ਫੀਲਡਾਂ ਵਾਂਗ) ਜਿਹਨਾਂ ਦਾ ਕੇਂਦਰ ਇੰਨਬਿੰਨ ਫੀਲਡ ਹੁੰਦਾ ਹੈ- ਐਕਸਟੈਂਸ਼ਨ ਫੀਲਡਾਂ ਦੇ ਗੈਰ-ਕਮਿਉਟੇਟਿਵ ਸਮਾਨ ਹੁੰਦੇ ਹਨ। ਅਤੇ ਸਧਾਰਣ ਰਿੰਗ ਸ਼ਾਖਾਵਾਂ ਤੋਂ ਜਿਆਦਾ ਪਾਬੰਧੀਆਂ ਵਾਲੇ ਹੁੰਦੇ ਹਨ। ਇਸ ਤੱਥ ਦੀ ਕਿ ਵਾਸਤਵਿਕਾਂ ਉੱਪਰ (ਬਰਾਬਰਤਾ ਤੱਕ), ਕੁਆਟ੍ਰਨੀਔਨ ਹੀ ਸਿਰਫ ਇਕਲੌਤੇ ਗੈਰ-ਸੂਖਮ CSA ਹੁੰਦੇ ਹਨ, ਇਸ ਤੱਥ ਨਾਲ ਤੁਲਨਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ਕਿ ਸਿਰਫ ਕੰਪਲੈਕਸ ਨੰਬਰ ਵਾਸਤਵਿਕਾਂ ਦੀ ਇਕਲੌਤੇ ਹੀ ਗੈਰ-ਸੂਖਮ ਫੀਲਡ ਸ਼ਾਖਾ ਹੁੰਦੇ ਹਨ।
ਹਵਾਲਾ ਪੁਸਤਕ ਸਮੱਗਰੀ
[ਸੋਧੋ]- “ਮੈਂ ਇਸ ਨੂੰ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਵਿੱਚ ਇੱਕ ਸ਼ੋਭਾਹੀਣ, ਜਾਂ ਅਧੂਰਾ ਕਹਾਂਗਾ, ਜਾਂ ਜਿਸ ਅਵਸਥਾ ਵਿੱਚ ਇਸਨੂੰ ਹੁਣ ਤੱਕ ਹਮੇਸ਼ਾਂ ਹੀ ਫਰੋਲਿਆ ਗਿਆ ਹੈ ਜਦੋਂ ਜਦੋਂ ਵੀ x, y, z ਅਦਿ ਦਾ ਸਹਾਰਾ ਲੈਣਾ ਜਰੂਰੀ ਹੋਇਆ ਜਾਂ ਹੁੰਦਾ ਦਿਸਿਆ ਹੈ”----ਵਿਲੀਅਮ ਰੋਵਨ ਹੈਮਿਲਟਨ (ਟੇਇਟ ਤੋਂ ਸੇਅਲੇਅ ਵੱਲ ਦੀ ਇੱਕ ਚਿੱਠੀ ਵਿੱਚ ਦਿੱਤੇ ਹੋਏ ਹਵਾਲੇ ਤੋਂ ਸੰਪਾਦਿਤ)
- “ਟਾਈਮ ਨੂੰ ਸਿਰਫ ਇੱਕ ਅਯਾਮ ਰੱਖਦਾ ਕਿਹਾ ਗਿਆ ਹੈ, ਅਤੇ ਸਪੇਸ ਨੂੰ ਤਿੰਨ ਅਯਾਮੀ ਕਿਹਾ ਗਿਆ ਹੈ। ਗਣਿਤਿਕ ਤੌਰ ਤੇ ਕੁਆਟ੍ਰਨੀਔਨ ਇਹਨਾਂ ਦੋਵੇਂ ਐਲੀਮੈਂਟਾਂ ਨੂੰ ਹਿੱਸਿਆਂ ਨੂੰ ਤਕਨੀਕੀ ਭਾਸ਼ਾ ਵਿੱਚ ਜੋੜਦਾ ਹੈ: ਜਿਸਨੂੰ “ਟਾਈਮ+ਸਪੇਸ”, ਜਾਂ “ਸਪੇਸ+ਟਾਈਮ” ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ: ਅਤੇ ਇਸ ਸਮਝ ਮੁਤਾਬਿਕ, ਇਸਦੀਆਂ ਜਾਂ ਘੱਟੋ ਘੱਟ ਇਸ ਵਿੱਚ ਚਾਰ ਅਯਾਮ ਸ਼ਾਮਿਲ ਹਨ। ਅਤੇ ਕਿਵੇਂ ਟਾਈਮ ਦੀ ਇੱਕ, ਸਪੇਸ ਦੇ ਤਿੰਨ ਨੂੰ ਚਿੰਨਾਂ ਦੀ ਚੇਨ ਵਿੱਚ ਲਪੇਟਿਆ ਹੋ ਸਕਦਾ ਹੈ” ----ਵਿਲੀਅਮ ਰੋਵਨ ਹੈਮਿਲਟਨ (ਆਰ.ਪੀ. ਗਰੇਵਜ਼ ਦੀ ਪੁਸਤਕ “ਲਾਈਫ ਔਫ ਸਰ ਵਿਲੀਅਮ ਰੋਵਨ ਹੈਮਿਲਟਨ” ਵਿੱਚੋਂ ਹਵਾਲਾ)
- “ਹੈਮਿਲਟਨ ਦੇ ਸੱਚਮੁੱਚ ਚੰਗੇ ਕੰਮ ਕਰਨ ਤੋਂ ਬਾਦ ਕੁਆਟ੍ਰਨੀਔਨ ਆਏ; ਅਤੇ, ਸੁੰਦਰ ਸਰਲਤਾ ਰਾਹੀਂ, ਉਹਨਾਂ ਲਈ ਇੱਕ ਅਮਿਸ਼ਰਿਤ ਨੁਕਸਾਨ ਰਹੇ ਹਨ ਜਿਹਨਾਂ ਨੇ ਇਹਨਾਂ ਨੂੰ ਕਿਸੇ ਤਰੀਕੇ ਛੂਹਿਆ, ਜਿਹਨਾਂ ਵਿੱਚ ਕਲੇਰਕ ਮੈਕਸਵੈੱਲ ਸ਼ਾਮਿਲ ਹੈ” ----ਲਾਰਡ ਕੈਲਵਿਨ, 1892
- “ਮੈਂ ਬਾਦ ਵਿੱਚ ਦੇਖ ਸਕਿਆ ਕਿ, ਜਿੱਥੇ ਤੱਕ ਮੇਰੀ ਜਰੂਰਤ ਦੇ ਵੈਕਟਰ ਵਿਸ਼ਲੇਸ਼ਣ ਦਾ ਸਬੰਧ ਹੈ, ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀ ਨਾ ਕੇਵਲ ਜਰੂਰਤ ਹੀ ਸੀ, ਸਗੋਂ ਨਾ ਵਿਚਾਰੇਜਾਣਯੋਗ ਮਾਤਰਾ ਦਾ ਇੱਕ ਪੌਜ਼ੇਟਿਵ ਨੁਕਸਾਨ ਸਨ; ਅਤੇ ਇਹਨਾਂ ਤੋਂ ਬਚਣ ਨਾਲ ਵੈਕਟਰ ਵਿਸ਼ਲੇਸ਼ਣ ਦੀ ਸਥਾਪਨਾ ਬਹੁਤ ਸਰਲ ਬਣਾਈ ਗਈ ਸੀ ਅਤੇ ਇਸਦੀ ਕਾਰਜ ਪ੍ਰਣਾਲੀ ਵੀ ਸਰਲ ਕੀਤੀ ਗਈ ਸੀ, ਅਤੇ ਇਹਨਾਂ ਦਾ ਸਧਾਰਣ ਕਾਰਟੀਜ਼ੀਅਨ ਕੰਮ ਨਾਲ ਸੁਵਿਧਾਪੂਰਵਕ ਮੇਲ ਕੀਤਾ ਜਾ ਸਕਦਾ ਸੀ” ----ਓਲੀਵਰ ਹੀਵੀਸਾਈਡ, ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਥਿਊਰੀ, ਵੌਲਿਉਮ 1, ਪੰਨਾ 134-135 (ਦੀ ਇਲੈਕਟ੍ਰੀਸ਼ੀਅਨ ਪ੍ਰਿੰਟਿੰਗ ਐਂਡ ਪਬਲਿਸ਼ਿੰਗ ਕੰਪਨੀ, ਲੰਡਨ, 1893)
- “ਨਾ ਹੀ ਮੈਟ੍ਰੀਸੀਜ਼ ਨਾ ਹੀ ਕੁਆਟ੍ਰਨੀਔਨ ਅਤੇ ਸਧਾਰਣ ਵੈਕਟਰ ਹੀ ਇਹਨਾਂ ਦਸ (ਵਾਧੂ) ਚੈਪਟਰਾਂ ਤੋਂ ਬਾਹਰ ਕੱਢੇ ਗਏ ਸਨ। ਮਾਡਰਨ ਟੈਂਸਰ ਕੈਲਕੁਲਸ ਦੀ ਨਿਰਵਿਰੋਧ ਤਾਕਤ ਦੇ ਬਾਵਜੂਦ, ਮੇਰੀ ਰਾਏ ਅਨੁਸਾਰ, ਸਪੈਸ਼ਲ ਰਿਲੇਟੀਵਿਟੀ ਦੇ ਮਨਾ ਕੀਤੇ ਹੋਏ ਖੇਤਰ ਵਿੱਚ ਵਸ਼ਿਸ਼ਟ ਲਾਭਾਂ ਦਾ ਪ੍ਰਸਤਾਵ ਰੱਖਣ ਲਈ,ਉਹ ਪੁਰਾਣੀਆਂ ਗਣਿਤਿਕ ਭਾਸ਼ਾਵਾਂ ਜਾਰੀ ਰਹਿੰਦੀਆਂ ਹਨ। ਹੋਰ ਤਾਂ ਹੋਰ, ਵਿਗਿਆਨ ਵਿੱਚ ਅਤੇ ਰੋਜ਼ਾਨਾ ਜਿੰਦਗੀ ਵਿੱਚ ਵੀ, ਇੱਕ ਭਾਸ਼ਾ ਤੋਂ ਜਿਆਦਾ ਭਾਸ਼ਾਵਾਂ ਦਾ ਅਨੁਭਵ ਕੀਮਤੀ ਹੁੰਦਾ ਹੈ, ਕਿਉਂਕਿ ਇਹ ਸਾਡੇ ਦ੍ਰਿਸ਼ਟੀਕੋਣਾਂ ਨੂੰ ਵਿਸ਼ਾਲ ਬਣਾਉਂਦਾ ਹੈ, ਸ਼ਬਦਾਂ ਜਾਂ ਗਣਿਤਿਕ ਚਿੰਨਾਂ ਰਾਹੀਂ ਦਰਸਾਏ ਪਦਾਰਥ ਦੀ ਹਾਇਪੋਟੇਸੀ (ਕਮਜੋਰ ਨੀਂਹ) ਵਿਰੁੱਧ ਰੱਖਿਆ ਕਰਨ ਅਨੁਕੂਲ ਅਤੇ ਅਲੋਚਨਾ ਅਨੁਕੂਲ ਹੁੰਦਾ ਹੈ” ---- ਲੁਡਵਿੱਕ ਸਿਲਬਰਸਟਨ, ਜੋ 1924 ਵਿੱਚ ਅਪਣੀ ਰਿਲੇਟੀਵਿਟੀ ਦੀ ਥਿਊਰੀ ਦਾ ਦੂਜਾ ਐਡੀਸ਼ਨ ਤਿਆਰ ਕਰ ਰਿਹਾ ਸੀ।
- “…ਗਣਿਤਿਕ ਵਿਚਾਰਾਂ ਦੇ ਸੰਘਰਸ਼-ਏ-ਜਿੰਦਗੀ ਵਿੱਚ ਇੱਕ ਅਸਫਲ ਜੀਵ ਦੇ ਰੂਪ ਵਿੱਚ, ਕੁਆਟ੍ਰਨੀਔਨ, ਉੰਨੀਵੀਂ ਸਦੀ ਮੁੱਕਣ ਦੀ ਹਵਾ ਨੂੰ ਪਸੀਜਦੇ ਲਗਦੇ ਹਨ। ਗਣਿਤ ਸ਼ਾਸਤਰੀ, ਮੰਨਦੇ ਹਨ ਕਿ ਉਹ ਅਜੇ ਵੀ ਅਪਣੇ ਦਿਲਾਂ ਵਿੱਚ ਕੁਆਟ੍ਰਨੀਔਨਾਂ ਦੀਆਂ ਵਿਚਾਰਯੋਗ ਅਲਜਬਰਿਕ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਲਈ ਇੱਕ ਗਰਮਜੋਸ਼ੀ ਵਾਲੀ ਜਗਹ ਰੱਖਦੇ ਹਨ, ਪਰ, ਕਾਸ਼! ਅਜਿਹੇ ਜੋਸ਼ ਦਾ ਸਖਤ-ਦਿਮਾਗ ਵਾਲੇ ਭੌਤਿਕੀ ਵਿਗਿਆਨੀ ਲਈ ਜਰਾ ਵੀ ਅਰਥ ਹੁੰਦਾ”--- ਸਿਮੋਨ ਐੱਲ. ਅਲਟਮਾੱਨ, 1986।
ਹਵਾਲਾ
[ਸੋਧੋ]- ↑ "Visualizing Quaternions". Morgan-Kaufmann/Elsevier. 2005.
- ↑ "Lce.hut.fi" (PDF). Archived from the original (PDF) on 2013-09-26. Retrieved 2015-11-06.
{{cite web}}: Unknown parameter|dead-url=ignored (|url-status=suggested) (help)






































![{\displaystyle [p,q]=2p\times q.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c45178772ffab33a9936c42a9df2be320f5d22b8)




































