ਸਮੱਗਰੀ 'ਤੇ ਜਾਓ

ਧਰੂਵੀ ਝੁਕਾਅ

ਵਿਕੀਪੀਡੀਆ, ਇੱਕ ਆਜ਼ਾਦ ਵਿਸ਼ਵਕੋਸ਼ ਤੋਂ
ਕਿਸੇ ਗ੍ਰਹਿ ਦੇ ਸਕਾਰਾਤਮਕ ਧਰੁਵ ਨੂੰ ਸੱਜੇ ਹੱਥ ਦੇ ਨਿਯਮ ਦੁਆਰਾ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈਃ ਜੇ ਸੱਜੇ ਹਾਥ ਦੀਆਂ ਉਂਗਲਾਂ ਘੁੰਮਣ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਘੁੰਮਦੀਆਂ ਹਨ ਤਾਂ ਅੰਗੂਠਾ ਸਕਾਰਾਤਮਕ ਧਰੁਵ ਵੱਲ ਇਸ਼ਾਰਾ ਕਰਦਾ ਹੈ। ਐਕਸੀਅਲ ਝੁਕਣ ਨੂੰ ਸਕਾਰਾਤਮਕ ਧਰੁਵ ਦੀ ਦਿਸ਼ਾ ਅਤੇ ਔਰਬਿਟਲ ਪਲੇਨ ਦੇ ਸਧਾਰਣ ਦੇ ਵਿਚਕਾਰ ਕੋਣ ਦੇ ਰੂਪ ਵਿੱਚ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਧਰਤੀ, ਯੂਰੇਨਸ ਅਤੇ ਸ਼ੁੱਕਰ ਦੇ ਕੋਣ ਕ੍ਰਮਵਾਰ ਲਗਭਗ 23°, 97° ਅਤੇ 177° ਹਨ।

ਖਗੋਲ ਵਿਗਿਆਨ ਵਿੱਚ, ਧੁਰੇ ਦਾ ਝੁਕਾਅ, ਜਿਸ ਨੂੰ ਤਿਰਛਾਪਣ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਕਿਸੇ ਵਸਤੂ ਦੇ ਘੁੰਮਣ ਵਾਲੇ ਧੁਰੇ ਅਤੇ ਇਸਦੇ ਚੱਕਰਵਰਤੀ ਧੁਰੇ ਦੇ ਵਿਚਕਾਰ ਦਾ ਕੋਣ ਹੈ, ਜੋ ਕਿ ਇਸਦੇ ਚੱਕਰਾਂ ਦੇ ਸਮਤਲ ਦੇ ਬਰਾਬਰ ਲੰਬਕਾਰੀ ਰੇਖਾ ਹੈ, ਇਹ ਇਸਦੇ ਭੂਮੱਧ ਰੇਖਾ ਅਤੇ ਚੱਕਰਾਂ ਵਿਚਕਾਰ ਦਾ ਕੋਣ ਹੁੰਦਾ ਹੈ।[1] ਇਹ ਔਰਬਿਟਲ ਝੁਕਾਅ ਤੋਂ ਵੱਖਰਾ ਹੈ।

0 ਡਿਗਰੀ ਦੀ ਤਿਰਛੀਤਾ ਉੱਤੇ, ਦੋਵੇਂ ਧੁਰਾ ਇੱਕੋ ਦਿਸ਼ਾ ਵੱਲ ਇਸ਼ਾਰਾ ਕਰਦੇ ਹਨ, ਅਰਥਾਤ, ਰੋਟੇਸ਼ਨਲ ਧੁਰਾ ਔਰਬਿਟਲ ਪਲੇਨ ਦੇ ਲੰਬਕਾਰੀ ਹੁੰਦਾ ਹੈ।

ਉਦਾਹਰਨ ਲਈ, ਧਰਤੀ ਦਾ ਰੋਟੇਸ਼ਨਲ ਧੁਰਾ ਇੱਕ ਕਾਲਪਨਿਕ ਰੇਖਾ ਹੈ ਜੋ ਉੱਤਰੀ ਧਰੁਵ ਅਤੇ ਦੱਖਣੀ ਧਰੁਵ ਦੋਵਾਂ ਵਿੱਚੋਂ ਲੰਘਦੀ ਹੈ, ਜਦੋਂ ਕਿ ਧਰਤੀ ਦਾ ਔਰਬਿਟਲ ਧੁਰਾ ਕਾਲਪਨਿਕ ਪਲੇਨ ਲਈ ਲੰਬਕਾਰੀ ਰੇਖਾ ਹੈ ਜਿਸ ਰਾਹੀਂ ਧਰਤੀ ਸੂਰਜ ਦੇ ਦੁਆਲੇ ਘੁੰਮਦੀ ਹੈ।

ਕਿਸੇ ਚੱਕਰੀ ਸਮੇਂ ਦੇ ਦੌਰਾਨ, ਤਿਰਛੀਤਾ ਆਮ ਤੌਰ ਉੱਤੇ ਕਾਫ਼ੀ ਨਹੀਂ ਬਦਲਦੀ, ਅਤੇ ਧੁਰੇ ਦੀ ਸਥਿਤੀ ਤਾਰਿਆਂ ਦੇ ਪਿਛੋਕਡ਼ ਦੇ ਮੁਕਾਬਲੇ ਇੱਕੋ ਜਿਹੀ ਰਹਿੰਦੀ ਹੈ। ਇਸ ਨਾਲ ਇੱਕ ਧਰੁਵ ਚੱਕਰ ਦੇ ਇੱਕ ਪਾਸੇ ਸੂਰਜ ਵੱਲ ਅਤੇ ਦੂਜੇ ਪਾਸੇ ਸੂਰਜ ਤੋਂ ਜ਼ਿਆਦਾ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ-ਜੋ ਧਰਤੀ ਉੱਤੇ ਮੌਸਮ ਦਾ ਕਾਰਨ ਹੈ।

ਮਿਆਰ

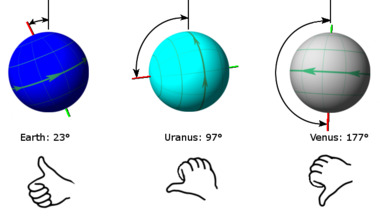
[ਸੋਧੋ]

ਕਿਸੇ ਗ੍ਰਹਿ ਦੇ ਝੁਕਾਅ ਨੂੰ ਨਿਰਧਾਰਤ ਕਰਨ ਦੇ ਦੋ ਮਿਆਰੀ ਤਰੀਕੇ ਹਨ। ਇੱਕ ਤਰੀਕਾ ਗ੍ਰਹਿ ਦੇ ਉੱਤਰੀ ਧਰੁਵ 'ਤੇ ਅਧਾਰਤ ਹੈ, ਜੋ ਧਰਤੀ ਦੇ ਉੱਤਰੀ ਧਰੁਵ ਦੀ ਦਿਸ਼ਾ ਦੇ ਸਬੰਧ ਵਿੱਚ ਪਰਿਭਾਸ਼ਿਤ ਹੈ, ਅਤੇ ਦੂਜਾ ਤਰੀਕਾ ਗ੍ਰਹਿ ਦੇ ਸਕਾਰਾਤਮਕ ਧਰੁਵ 'ਤੇ ਅਧਾਰਤ ਹੈ, ਸੱਜੇ ਹੱਥ ਦੇ ਨਿਯਮ ਦੁਆਰਾ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਗਿਆ ਹੈ:

  • ਅੰਤਰਰਾਸ਼ਟਰੀ ਖਗੋਲ ਵਿਗਿਆਨ ਸੰਘ (ਆਈ. ਏ. ਯੂ.) ਕਿਸੇ ਗ੍ਰਹਿ ਦੇ ਉੱਤਰੀ ਧਰੁਵ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰਦਾ ਹੈ ਜੋ ਕਿ ਸੂਰਜੀ ਪ੍ਰਣਾਲੀ ਦੇ ਸਥਿਰ ਪਲੇਨ ਦੇ ਧਰਤੀ ਦੇ ਉੱਤਰ ਵਾਲੇ ਪਾਸੇ ਸਥਿਤ ਹੈ ਇਸ ਪ੍ਰਣਾਲੀ ਦੇ ਤਹਿਤ, ਸ਼ੁੱਕਰ 3 ° ਝੁਕਿਆ ਹੋਇਆ ਹੈ ਅਤੇ ਦੂਜੇ ਗ੍ਰਹਿਆਂ ਦੇ ਉਲਟ, ਪ੍ਰਤੀਗਾਮੀ ਘੁੰਮਦਾ ਹੈ।[2][3][4]
  • ਆਈਏਯੂ ਸਥਿਤੀ ਨਿਰਧਾਰਤ ਕਰਨ ਦੇ ਉਦੇਸ਼ ਲਈ ਇੱਕ ਸਕਾਰਾਤਮਕ ਧਰੁਵ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰਨ ਲਈ ਸੱਜੇ ਹੱਥ ਦੇ ਨਿਯਮ ਦੀ ਵਰਤੋਂ ਵੀ ਕਰਦਾ ਹੈ।[5] ਇਸ ਪਰੰਪਰਾ ਦੀ ਵਰਤੋਂ ਕਰਦਿਆਂ, ਸ਼ੁੱਕਰ 177° ਝੁਕਿਆ ਹੋਇਆ ਹੈ ਅਤੇ ਅਗਾਂਹ ਵੱਲ ਘੁੰਮਦਾ ਹੈ।

ਧਰਤੀ

[ਸੋਧੋ]

ਧਰਤੀ ਦੇ ਚੱਕਰਵਰਤੀ ਪਲੇਨ ਨੂੰ ਚੱਕਰਵਾਤ ਪਲੇਨ ਵਜੋਂ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ, ਅਤੇ ਧਰਤੀ ਦੇ ਝੁਕਾਅ ਨੂੰ ਖਗੋਲ ਵਿਗਿਆਨੀਆਂ ਦੁਆਰਾ ਚੱਕਰਵਾਤ ਦੀ ਤਿਰਛੀਤਾ ਵਜੋਂ ਜਾਣਿਆ ਜਾਂਦਾ, ਜੋ ਕਿ ਚੱਕਰ ਅਤੇ ਸਵਰਗੀ ਭੂਮੱਧ ਰੇਖਾ ਦੇ ਵਿਚਕਾਰ ਦਾ ਕੋਣ ਹੈ।[6] ਇਸ ਨੂੰ ਯੂਨਾਨੀ ਅੱਖਰ ε ਦੁਆਰਾ ਦਰਸਾਇਆ ਗਿਆ ਹੈ।

ਵਰਤਮਾਨ ਵਿੱਚ ਧਰਤੀ ਦਾ ਇੱਕ ਧੁਰੇ ਵਾਲਾ ਝੁਕਾਅ ਲਗਭਗ 23.44 ° ਹੈ।[7] ਇਹ ਮੁੱਲ ਧੁਰੇ ਦੀ ਪੂਰਵ-ਗਤੀ ਦੇ ਚੱਕਰ ਦੌਰਾਨ ਇੱਕ ਸਥਿਰ ਔਰਬਿਟਲ ਪਲੇਨ ਦੇ ਸਬੰਧ ਵਿੱਚ ਲਗਭਗ ਇੱਕੋ ਜਿਹਾ ਰਹਿੰਦਾ ਹੈ।[8] ਪਰ ਚੱਕਰਵਾਤੀ (ਅਰਥਾਤ, ਧਰਤੀ ਦਾ ਚੱਕਰ ਗ੍ਰਹੀਆਂ ਦੇ ਗਡ਼ਬਡ਼ੀ ਕਾਰਨ ਚਲਦਾ ਹੈ, ਅਤੇ ਚੱਕਰਵਰਤੀ ਦੀ ਤਿਰਛੀਤਾ ਇੱਕ ਨਿਸ਼ਚਿਤ ਮਾਤਰਾ ਨਹੀਂ ਹੈ। ਵਰਤਮਾਨ ਵਿੱਚ, ਇਹ ਪ੍ਰਤੀ ਸਦੀ ਲਗਭਗ 46.8′′ ਦੀ ਦਰ ਨਾਲ ਘਟ ਰਿਹਾ ਹੈ (ਹੇਠਾਂ ਥੋਡ਼੍ਹੇ ਸਮੇਂ ਵਿੱਚ ਵੇਰਵੇ ਵੇਖੋ) ।[9]

ਇਤਿਹਾਸ

[ਸੋਧੋ]

ਪ੍ਰਾਚੀਨ ਯੂਨਾਨੀਆਂ ਕੋਲ ਲਗਭਗ 350 ਬੀ. ਸੀ. ਤੋਂ ਤਿਰਛੀਤਾ ਦਾ ਚੰਗਾ ਮਾਪ ਸੀ, ਜਦੋਂ ਮਾਰਸੇਲਜ਼ ਦੇ ਪਾਈਥੀਅਸ ਨੇ ਗਰਮੀਆਂ ਦੀ ਸੰਗਰਾਮ ਵਿੱਚ ਇੱਕ ਗਨੋਮੋਨ ਦੇ ਪਰਛਾਵੇਂ ਨੂੰ ਮਾਪਿਆ ਸੀ।[10] ਲਗਭਗ 830 ਈਸਵੀ ਵਿੱਚ, ਬਗਦਾਦ ਦੇ ਖਲੀਫਾ ਅਲ-ਮਾਮੂਨ ਨੇ ਆਪਣੇ ਖਗੋਲ ਵਿਗਿਆਨੀਆਂ ਨੂੰ ਤਿਰਛੀਤਾ ਨੂੰ ਮਾਪਣ ਦਾ ਨਿਰਦੇਸ਼ ਦਿੱਤਾ, ਅਤੇ ਨਤੀਜਾ ਅਰਬ ਸੰਸਾਰ ਵਿੱਚ ਕਈ ਸਾਲਾਂ ਤੱਕ ਵਰਤਿਆ ਗਿਆ।[11] 1437 ਵਿੱਚ, ਉਲੁਗ ਬੇਗ ਨੇ ਧਰਤੀ ਦੇ ਧੁਰੇ ਦੇ ਝੁਕਾਅ ਨੂੰ 23°30′17′′ (ID1) ° ਦੇ ਰੂਪ ਵਿੱਚ ਨਿਰਧਾਰਤ ਕੀਤਾ।[12]

ਮੱਧ ਯੁੱਗ ਦੇ ਦੌਰਾਨ, ਇਹ ਵਿਆਪਕ ਤੌਰ ਤੇ ਮੰਨਿਆ ਜਾਂਦਾ ਸੀ ਕਿ ਪ੍ਰੀਸੈਸ਼ਨ ਅਤੇ ਧਰਤੀ ਦੀ ਤਿਰਛੀਤਾ ਦੋਵੇਂ ਇੱਕ ਔਸਤ ਮੁੱਲ ਦੇ ਦੁਆਲੇ ਘੁੰਮਦੀਆਂ ਹਨ, 672 ਸਾਲਾਂ ਦੀ ਮਿਆਦ ਦੇ ਨਾਲ, ਇੱਕ ਵਿਚਾਰ ਜਿਸ ਨੂੰ ਇਕੁਇਨੋਕਸ ਦੀ ਘਬਰਾਹਟ ਵਜੋਂ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ। ਸ਼ਾਇਦ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਇਹ ਅਹਿਸਾਸ ਹੋਇਆ ਕਿ ਇਹ ਗਲਤ ਸੀ (ਇਤਿਹਾਸਕ ਸਮੇਂ ਦੌਰਾਨ) ਚੌਦਵੀਂ ਸਦੀ ਵਿੱਚ ਇਬਨ ਅਲ-ਸ਼ਾਤਿਰ ਸੀ ਅਤੇ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਮਹਿਸੂਸ ਕਰਨ ਵਾਲਾ ਸੀ ਕਿ 1538 ਵਿੱਚ ਫਰਕਾਸਟੋਰੋ ਮੁਕਾਬਲਤਨ ਸਥਿਰ ਦਰ ਨਾਲ ਘਟ ਰਿਹਾ ਹੈ।[13][14] ਤਿਰਛੀਤਾ ਦੇ ਪਹਿਲੇ ਸਹੀ, ਆਧੁਨਿਕ, ਪੱਛਮੀ ਨਿਰੀਖਣ ਸ਼ਾਇਦ ਡੈਨਮਾਰਕ ਦੇ ਟਾਈਕੋ ਬ੍ਰਾਹੇ ਦੇ ਸਨ, ਲਗਭਗ 1584, ਹਾਲਾਂਕਿ ਅਲ-ਮਮੂਨ, ਅਲ-ਤੁਸੀ, ਪੁਰਬਾਚ, ਰੈਜੀਓਮੋਂਟਨਸ ਅਤੇ ਵਾਲਥਰ ਸਮੇਤ ਕਈ ਹੋਰਾਂ ਦੁਆਰਾ ਨਿਰੀਖਣ, ਸਮਾਨ ਜਾਣਕਾਰੀ ਪ੍ਰਦਾਨ ਕਰ ਸਕਦੇ ਸਨ।[15][16]

ਸੀਜ਼ਨ

[ਸੋਧੋ]
ਧਰਤੀ ਦਾ ਧੁਰਾ ਪਿਛੋਕਡ਼ ਦੇ ਤਾਰਿਆਂ ਦੇ ਸੰਦਰਭ ਵਿੱਚ ਉਸੇ ਦਿਸ਼ਾ ਵਿੱਚ ਸਥਿਤ ਰਹਿੰਦਾ ਹੈ ਭਾਵੇਂ ਇਹ ਆਪਣੇ ਚੱਕਰ ਵਿੱਚ ਕਿੱਥੇ ਹੈ। ਉੱਤਰੀ ਗੋਲਿਸਫਾਇਰ ਦੀ ਗਰਮੀ ਇਸ ਚਿੱਤਰ ਦੇ ਸੱਜੇ ਪਾਸੇ ਹੁੰਦੀ ਹੈ, ਜਿੱਥੇ ਉੱਤਰੀ ਧਰੁਵ (ਲਾਲ) ਸੂਰਜ ਵੱਲ, ਸਰਦੀਆਂ ਖੱਬੇ ਪਾਸੇ ਹੁੰਦੀਆਂ ਹਨ।

ਧਰਤੀ ਦਾ ਧੁਰਾ ਇੱਕ ਸਾਲ ਦੌਰਾਨ ਪਿਛੋਕਡ਼ ਦੇ ਤਾਰਿਆਂ ਦੇ ਸੰਦਰਭ ਵਿੱਚ ਇੱਕੋ ਦਿਸ਼ਾ ਵਿੱਚ ਝੁਕਿਆ ਰਹਿੰਦਾ ਹੈ (ਜਿੰਨਾ ਇਹ ਜਾਇਰੋਸਕੋਪ ਪ੍ਰਭਾਵ ਕਾਰਨ ਆਪਣੇ ਚੱਕਰ ਵਿੱਚ ਹੈ) । ਇਸ ਦਾ ਮਤਲਬ ਹੈ ਕਿ ਇੱਕ ਧਰੁਵ (ਅਤੇ ਧਰਤੀ ਨਾਲ ਸੰਬੰਧਿਤ ਅਰਧਗੋਲੇ ਨੂੰ ਚੱਕਰ ਦੇ ਇੱਕ ਪਾਸੇ ਸੂਰਜ ਤੋਂ ਦੂਰ ਭੇਜਿਆ ਜਾਵੇਗਾ, ਅਤੇ ਅੱਧਾ ਚੱਕਰ ਬਾਅਦ ਵਿੱਚ (ਅੱਧੇ ਸਾਲ ਬਾਅਦ) ਇਹ ਧਰੁਵ ਸੂਰਜ ਵੱਲ ਨਿਰਦੇਸ਼ਿਤ ਕੀਤਾ ਜਾਵੇਗਾ। ਇਹ ਧਰਤੀ ਦੇ ਮੌਸਮ ਦਾ ਕਾਰਨ ਹੈ। ਗਰਮੀਆਂ ਉੱਤਰੀ ਗੋਲਿਸਫਾਇਰ ਵਿੱਚ ਹੁੰਦੀਆਂ ਹਨ ਜਦੋਂ ਉੱਤਰੀ ਧਰੁਵ ਸੂਰਜ ਵੱਲ ਜਾਂਦਾ ਹੈ। ਧਰਤੀ ਦੇ ਧੁਰੇ ਦੇ ਝੁਕਾਅ ਵਿੱਚ ਭਿੰਨਤਾਵਾਂ ਮੌਸਮ ਨੂੰ ਪ੍ਰਭਾਵਤ ਕਰ ਸਕਦੀਆਂ ਹਨ ਅਤੇ ਸੰਭਾਵਤ ਤੌਰ ਤੇ ਲੰਬੇ ਸਮੇਂ ਦੇ ਮੌਸਮ ਵਿੱਚ ਤਬਦੀਲੀ ਦਾ ਇੱਕ ਕਾਰਕ ਹੈ (ਮਿਲਾਨਕੋਵਿਚ ਚੱਕਰ ਵੀ ਵੇਖੋ) ।

ਧਰਤੀ ਦੇ ਧੁਰੀ ਝੁਕਾਅ (ε) ਅਤੇ ਖੰਡੀ ਅਤੇ ਧਰੁਵੀ ਚੱਕਰਾਂ ਵਿਚਕਾਰ ਸਬੰਧ

ਔਕਸੀਲੇਸ਼ਨ

[ਸੋਧੋ]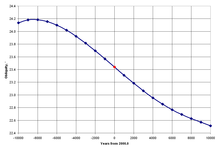
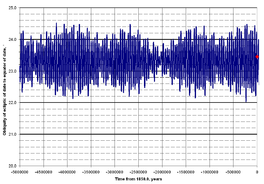
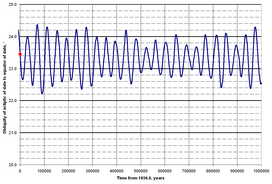
ਲਾਸ੍ਕਰ (1986) ਤੋਂ 20,000 ਸਾਲਾਂ ਲਈ ਚੱਕਰ ਦੀ ਓਬਲਿਕੁਇਟੀ। ਲਾਲ ਬਿੰਦੂ ਸਾਲ 2000 ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ।

ਤਿਰਛੀ ਦਾ ਸਹੀ ਕੋਣੀ ਮੁੱਲ ਕਈ ਸਾਲਾਂ ਤੋਂ ਧਰਤੀ ਅਤੇ ਗ੍ਰਹਿ ਦੀਆਂ ਗਤੀ ਦੇ ਨਿਰੀਖਣ ਦੁਆਰਾ ਪਾਇਆ ਜਾਂਦਾ ਹੈ। ਖਗੋਲ ਵਿਗਿਆਨੀ ਨਵੇਂ ਬੁਨਿਆਦੀ ਐਫੀਮਰਾਈਡਸ ਪੈਦਾ ਕਰਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਨਿਰੀਖਣ ਦੀ ਸ਼ੁੱਧਤਾ ਵਿੱਚ ਸੁਧਾਰ ਹੁੰਦਾ ਹੈ ਅਤੇ ਜਿਵੇਂ ਜਿਵੇਂ ਗਤੀਸ਼ੀਲਤਾ ਦੀ ਸਮਝ ਵਧਦੀ ਹੈ, ਅਤੇ ਇਨ੍ਹਾਂ ਐਫੀਮਲਾਈਡਸ ਤੋਂ ਤਿਰਛੀਤਾ ਸਮੇਤ ਵੱਖ-ਵੱਖ ਖਗੋਲ-ਵਿਗਿਆਨਕ ਮੁੱਲ ਪ੍ਰਾਪਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ।

ਸਲਾਨਾ ਪੰਨੇ ਪ੍ਰਕਾਸ਼ਿਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਪ੍ਰਾਪਤ ਮੁੱਲਾਂ ਅਤੇ ਵਰਤੋਂ ਦੇ ਤਰੀਕਿਆਂ ਦੀ ਸੂਚੀ ਹੁੰਦੀ ਹੈ। 1983 ਤੱਕ, ਕਿਸੇ ਵੀ ਮਿਤੀ ਲਈ ਔਸਤ ਤਿਰਛੀਤਾ ਦੇ ਖਗੋਲ ਵਿਗਿਆਨ ਅਲਮਾਨਕ ਦੇ ਕੋਣੀ ਮੁੱਲ ਦੀ ਗਣਨਾ ਨਿਊਕੌਂਬ ਦੇ ਕੰਮ ਦੇ ਅਧਾਰ ਤੇ ਕੀਤੀ ਗਈ ਸੀ, ਜਿਸ ਨੇ ਲਗਭਗ 1895 ਤੱਕ ਗ੍ਰਹਿਆਂ ਦੀ ਸਥਿਤੀ ਦਾ ਵਿਸ਼ਲੇਸ਼ਣ ਕੀਤਾ ਸੀ।

ε = 23°27′8.26″ − 46.845″ T − 0.0059″ T2 + 0.00181″ T3

ਜਿੱਥੇ ε ਤਿਰਛੀ ਹੈ ਅਤੇ T, B1900.0 ਤੋਂ ਲੈ ਕੇ ਪ੍ਰਸ਼ਨ ਵਿੱਚ ਮਿਤੀ ਤੱਕ ਦੀਆਂ ਗਰਮ ਖੰਡੀ ਸਦੀਆਂ ਹਨ।[17]

1984 ਤੋਂ, ਜੈੱਟ ਪ੍ਰੋਪਲਸ਼ਨ ਲੈਬਾਰਟਰੀ ਦੀ ਕੰਪਿਊਟਰ ਦੁਆਰਾ ਤਿਆਰ ਕੀਤੀ ਗਈ ਐਫੀਮਰਾਈਡਜ਼ ਦੀ ਡੀ. ਈ. ਲਡ਼ੀ ਨੇ ਖਗੋਲ ਵਿਗਿਆਨ ਅਲਮਾਨਕ ਦੇ ਬੁਨਿਆਦੀ ਐਫੀਮਰਿਸ ਵਜੋਂ ਕੰਮ ਸੰਭਾਲਿਆ। DE200 ਉੱਤੇ ਅਧਾਰਿਤ ਓਬਲਿਕੁਇਟੀ, ਜਿਸ ਨੇ 1911 ਤੋਂ 1979 ਤੱਕ ਦੇ ਨਿਰੀਖਣਾਂ ਦਾ ਵਿਸ਼ਲੇਸ਼ਣ ਕੀਤਾ, ਦੀ ਗਣਨਾ ਕੀਤੀ ਗਈ ਸੀਃ

ε = 23°26′21.448″ − 46.8150″ T − 0.00059″ T2 + 0.001813″ T3

ਜਿੱਥੇ ਇਸ ਤੋਂ ਬਾਅਦ T J2000.0 ਤੋਂ ਜੂਲੀਅਨ ਸਦੀ ਹੈ।[18]

ਜੇ. ਪੀ. ਐੱਲ. ਦੇ ਬੁਨਿਆਦੀ ਇਫੇਮਰਾਈਡਸ ਨੂੰ ਲਗਾਤਾਰ ਅੱਪਡੇਟ ਕੀਤਾ ਗਿਆ ਹੈ। ਉਦਾਹਰਨ ਲਈ, 2006 ਵਿੱਚ ਆਈਏਯੂ ਦੇ ਮਤੇ ਅਨੁਸਾਰ ਪੀ 03 ਖਗੋਲ-ਵਿਗਿਆਨਕ ਮਾਡਲ ਦੇ ਹੱਕ ਵਿੱਚ, 2010 ਲਈ ਖਗੋਲ-ਵਿਗਿਆਨਕ ਪੰਨੇ ਨਿਰਧਾਰਤ ਕਰਦਾ ਹੈਃ [19]

ε = 23°26′21.406″ − 46.836769″ T − 0.0001831″ T2 + 0.00200340″ T3 − 5.76″ × 10−7 T4 − 4.34″ × 10−8 T5

ਤਿਰਛੀਤਾ ਲਈ ਇਹ ਸਮੀਕਰਨ ਇੱਕ ਮੁਕਾਬਲਤਨ ਥੋਡ਼ੇ ਸਮੇਂ ਦੀ ਮਿਆਦ ਵਿੱਚ ਉੱਚ ਸ਼ੁੱਧਤਾ ਲਈ ਤਿਆਰ ਕੀਤੇ ਗਏ ਹਨ, ਸ਼ਾਇਦ ± ਕਈ ਸਦੀਆਂ.[20] ਜੈਕਸ ਲਾਸਕਰ ਨੇ 1000 ਸਾਲਾਂ ਵਿੱਚ T10 ਚੰਗੇ ਨੂੰ 0.02 "ਅਤੇ 10,000 ਸਾਲਾਂ ਵਿੱਚੋਂ ਕਈ ਆਰਕ ਸਕਿੰਟ ਲਈ ਆਰਡਰ ਕਰਨ ਲਈ ਇੱਕ ਸਮੀਕਰਨ ਦੀ ਗਣਨਾ ਕੀਤੀ।

ε = 23°26′21.448″ − 4680.93″ t − 1.55″ t2 + 1999.25″ t3 − 51.38″ t4 − 249.67″ t5 − 39.05″ t6 + 7.12″ t7 + 27.87″ t8 + 5.79″ t9 + 2.45″ t10

ਇਹ ਸਮੀਕਰਨ ਅਖੌਤੀ ਮੀਨ ਤਿਰਛੀਤਾ ਲਈ ਹਨ, ਅਰਥਾਤ, ਛੋਟੀ ਮਿਆਦ ਦੇ ਭਿੰਨਤਾਵਾਂ ਤੋਂ ਮੁਕਤ ਤਿਰਛੀਤਾ। ਚੰਦਰਮਾ ਅਤੇ ਧਰਤੀ ਦੀਆਂ ਇਸ ਦੇ ਚੱਕਰ ਵਿੱਚ ਆਵਰਤੀ ਗਤੀ ਬਹੁਤ ਘੱਟ (9.2 ਚੱਕਰ ਸਕਿੰਟ) ਛੋਟੀ ਮਿਆਦ ਦਾ ਕਾਰਨ ਬਣਦੀ ਹੈ (ਧਰਤੀ ਦੇ ਘੁੰਮਣ ਵਾਲੇ ਧੁਰੇ ਦੇ ਲਗਭਗ 18.6 ਸਾਲ), ਜਿਸ ਨੂੰ ਨਿਊਟੇਸ਼ਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਜੋ ਧਰਤੀ ਦੀ ਤਿਰਛੀਤਾ ਵਿੱਚ ਇੱਕ ਆਵਰਤੀ ਹਿੱਸਾ ਜੋਡ਼ਦਾ ਹੈ।[21][22] ਸੱਚੀ ਜਾਂ ਤੁਰੰਤ ਤਿਰਛੀਤਾ ਵਿੱਸੱਚ ਹੈ। ਨਿਊਟੇਸ਼ਨ ਸ਼ਾਮਲ ਹੈ।[23]

ਲੰਬੇ ਮਿਆਦ

[ਸੋਧੋ]

ਕਈ ਮਿਲੀਅਨ ਸਾਲਾਂ ਦੀ ਮਿਆਦ ਵਿੱਚ ਸੂਰਜੀ ਪ੍ਰਣਾਲੀ ਦੇ ਵਿਵਹਾਰ ਦੀ ਨਕਲ ਕਰਨ ਲਈ ਸੰਖਿਆਤਮਕ ਤਰੀਕਿਆਂ ਦੀ ਵਰਤੋਂ ਕਰਦਿਆਂ, ਧਰਤੀ ਦੇ ਚੱਕਰ ਵਿੱਚ ਲੰਬੇ ਸਮੇਂ ਦੀਆਂ ਤਬਦੀਲੀਆਂ ਅਤੇ ਇਸ ਲਈ ਇਸ ਦੀ ਤਿਰਛੀਤਾ ਦੀ ਜਾਂਚ ਕੀਤੀ ਗਈ ਹੈ। ਪਿਛਲੇ 5 ਮਿਲੀਅਨ ਸਾਲਾਂ ਤੋਂ, ਧਰਤੀ ਦੀ ਤਿਰਛੀਤਾ 22°2′33′′ ਅਤੇ 24°30′16′′ ਦੇ ਵਿਚਕਾਰ ਹੈ, ਜਿਸ ਦੀ ਔਸਤ ਮਿਆਦ 41,040 ਸਾਲ ਹੈ। ਇਹ ਚੱਕਰ ਪੂਰਵ-ਗਤੀ ਦਾ ਇੱਕ ਸੁਮੇਲ ਹੈ ਅਤੇ ਚੱਕਰ ਦੀ ਗਤੀ ਵਿੱਚ ਸਭ ਤੋਂ ਵੱਡਾ ਸ਼ਬਦ ਹੈ। ਅਗਲੇ 10 ਲੱਖ ਸਾਲਾਂ ਲਈ, ਇਹ ਚੱਕਰ 22°13′44′′ ਅਤੇ 24°20′50′′ ਦੇ ਵਿਚਕਾਰ ਤਿਰਛੀਤਾ ਨੂੰ ਲੈ ਕੇ ਜਾਵੇਗਾ।[24]

ਚੰਦਰਮਾ ਦਾ ਧਰਤੀ ਦੀ ਤਿਰਛੀਤਾ ਉੱਤੇ ਸਥਿਰ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ। 1993 ਵਿੱਚ ਕੀਤੇ ਗਏ ਫ੍ਰੀਕੁਐਂਸੀ ਨਕਸ਼ੇ ਦੇ ਵਿਸ਼ਲੇਸ਼ਣ ਨੇ ਸੁਝਾਅ ਦਿੱਤਾ ਕਿ, ਚੰਦਰਮਾ ਦੀ ਗੈਰਹਾਜ਼ਰੀ ਵਿੱਚ, ਚੱਕਰਵਰਤੀ ਗੂੰਜ ਅਤੇ ਸੂਰਜੀ ਪ੍ਰਣਾਲੀ ਦੇ ਹਫਡ਼ਾ-ਦਫਡ਼ੀ ਵਾਲੇ ਵਿਵਹਾਰ ਕਾਰਨ ਤਿਰਛੀਤਾ ਤੇਜ਼ੀ ਨਾਲ ਬਦਲ ਸਕਦੀ ਹੈ, ਜੋ ਕਿ ਕੁਝ ਮਿਲੀਅਨ ਸਾਲਾਂ ਵਿੱਚ 90 ° ਤੱਕ ਪਹੁੰਚ ਸਕਦੀ ਹੈ (ਚੰਦਰਮੇ ਦਾ ਚੱਕਰ ਵੀ ਵੇਖੋ) ।[25][26] ਹਾਲਾਂਕਿ, 2011 ਵਿੱਚ ਕੀਤੇ ਗਏ ਹੋਰ ਤਾਜ਼ਾ ਸੰਖਿਆਤਮਕ ਸਿਮੂਲੇਸ਼ਨ ਨੇ ਸੰਕੇਤ ਦਿੱਤਾ ਕਿ ਚੰਦਰਮਾ ਦੀ ਗੈਰਹਾਜ਼ਰੀ ਵਿੱਚ ਵੀ, ਧਰਤੀ ਦੀ ਤਿਰਛੀਤਾ ਲਗਭਗ 20-25 ° ਨਾਲ ਬਦਲਦੀ ਨਹੀਂ ਹੋ ਸਕਦੀ।[27] ਇਸ ਵਿਰੋਧਾਭਾਸ ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ, ਤਿਰਛੀ ਦੀ ਫੈਲਾਅ ਦਰ ਦੀ ਗਣਨਾ ਕੀਤੀ ਗਈ ਹੈ, ਅਤੇ ਇਹ ਪਾਇਆ ਗਿਆ ਹੈ ਕਿ ਧਰਤੀ ਦੀ ਤਿਰਛੀਤਾ ਨੂੰ 90 ° ਦੇ ਨੇਡ਼ੇ ਪਹੁੰਚਣ ਵਿੱਚ ਅਰਬਾਂ ਤੋਂ ਵੱਧ ਸਾਲ ਲੱਗਦੇ ਹਨ।[28] ਚੰਦਰਮਾ ਦਾ ਸਥਿਰ ਪ੍ਰਭਾਵ ਦੋ ਅਰਬ ਤੋਂ ਵੀ ਘੱਟ ਸਾਲਾਂ ਤੱਕ ਜਾਰੀ ਰਹੇਗਾ। ਜਿਵੇਂ ਕਿ ਚੰਦਰਮਾ ਜਵਾਰ-ਭਾਟਾ ਪ੍ਰਵੇਗ ਦੇ ਕਾਰਨ ਧਰਤੀ ਤੋਂ ਪਿੱਛੇ ਹਟਣਾ ਜਾਰੀ ਰੱਖਦਾ ਹੈ, ਗੂੰਜ ਹੋ ਸਕਦੀ ਹੈ ਜੋ ਤਿਰਛੀ ਦੇ ਵੱਡੇ oscillations ਦਾ ਕਾਰਨ ਬਣ ਸਕਦੀ ਹੈ. [29]

Long-term obliquity of the ecliptic. Left: for the past 5 million years; the obliquity varies only from about 22.0° to 24.5°. Right: for the next 1 million years; note the approx. 41,000-year period of variation. In both graphs, the red point represents the year 1850.[30]

ਸੂਰਜੀ ਪ੍ਰਣਾਲੀ ਦੇ ਸਰੀਰ

[ਸੋਧੋ]
ਅੱਠ ਗ੍ਰਹਿ ਅਤੇ ਦੋ ਬੌਣੇ ਗ੍ਰਹਿਆਂ, ਸੇਰੇਸ ਅਤੇ ਪਲੂਟੋ ਦਾ ਧੁਰੇ ਝੁਕਾਅ

ਸੌਰ ਮੰਡਲ ਦੇ ਸਾਰੇ ਚਾਰ ਅੰਦਰੂਨੀ, ਪਥਰੀਲੇ ਗ੍ਰਹਿਆਂ ਵਿੱਚ ਅਤੀਤ ਵਿੱਚ ਉਨ੍ਹਾਂ ਦੀ ਤਿਰਛੀਤਾ ਵਿੱਚ ਵੱਡੇ ਪਰਿਵਰਤਨ ਹੋਏ ਹੋਣਗੇ। ਕਿਉਂਕਿ ਤਿਰਛੀਤਾ ਘੁੰਮਣ ਦੇ ਧੁਰੇ ਅਤੇ ਔਰਬਿਟਲ ਪਲੇਨ ਦੇ ਲੰਬਕਾਰੀ ਦਿਸ਼ਾ ਦੇ ਵਿਚਕਾਰ ਦਾ ਕੋਣ ਹੈ, ਇਹ ਦੂਜੇ ਗ੍ਰਹਿਆਂ ਦੇ ਪ੍ਰਭਾਵ ਕਾਰਨ ਔਰਬਿਟਲ ਪ੍ਲੇਨ ਦੇ ਬਦਲਣ ਨਾਲ ਬਦਲਦਾ ਹੈ। ਪਰ ਘੁੰਮਣ ਦਾ ਧੁਰਾ ਕਿਸੇ ਗ੍ਰਹਿ ਦੇ ਭੂਮੱਧ ਰੇਖਾ ਉੱਤੇ ਸੂਰਜ ਦੁਆਰਾ ਲਗਾਏ ਗਏ ਟਾਰਕ ਦੇ ਕਾਰਨ ਵੀ ਚਲ ਸਕਦਾ ਹੈ। ਧਰਤੀ ਵਾਂਗ, ਸਾਰੇ ਪਥਰੀਲੇ ਗ੍ਰਹਿ ਧੁਰੇ ਦੀ ਪੂਰਵ-ਗਤੀ ਦਿਖਾਉਂਦੇ ਹਨ। ਜੇਕਰ ਪ੍ਰੀਸੈਸ਼ਨ ਰੇਟ ਬਹੁਤ ਤੇਜ਼ ਹੁੰਦੀ ਤਾਂ ਤਿਰਛੀ ਅਸਲ ਵਿੱਚ ਕਾਫ਼ੀ ਸਥਿਰ ਰਹਿੰਦੀ ਭਾਵੇਂ ਕਿ ਔਰਬਿਟਲ ਪਲੇਨ ਬਦਲਦਾ ਹੈ।[31] ਇਹ ਦਰ ਹੋਰ ਚੀਜ਼ਾਂ ਦੇ ਨਾਲ-ਨਾਲ ਜਵਾਰ-ਭਾਟਾ ਦੇ ਖਾਤਮੇ ਅਤੇ ਕੋਰ-ਮੈਂਟਲ ਪਰਸਪਰ ਪ੍ਰਭਾਵ ਦੇ ਕਾਰਨ ਵੱਖਰੀ ਹੁੰਦੀ ਹੈ। ਜਦੋਂ ਕਿਸੇ ਗ੍ਰਹਿ ਦੀ ਪੂਰਵ-ਗਤੀ ਦਰ ਕੁਝ ਮੁੱਲਾਂ ਦੇ ਨੇਡ਼ੇ ਪਹੁੰਚਦੀ ਹੈ, ਤਾਂ ਔਰਬਿਟਲ ਰੈਜ਼ੋਨੈਂਸ ਤਿਰਛੀਤਾ ਵਿੱਚ ਵੱਡੀਆਂ ਤਬਦੀਲੀਆਂ ਦਾ ਕਾਰਨ ਬਣ ਸਕਦੀ ਹੈ। ਗੂੰਜਦੀਆਂ ਦਰਾਂ ਵਿੱਚੋਂ ਇੱਕ ਹੋਣ ਵਾਲੇ ਯੋਗਦਾਨ ਦਾ ਵਿਸਤਾਰ ਗੂੰਜਦੀ ਦਰ ਅਤੇ ਪੂਰਵ-ਗਤੀ ਦਰ ਦੇ ਵਿੱਚ ਅੰਤਰ ਨਾਲ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ, ਇਸ ਲਈ ਇਹ ਉਦੋਂ ਵੱਡਾ ਹੋ ਜਾਂਦਾ ਹੈ ਜਦੋਂ ਦੋਵੇਂ ਇੱਕੋ ਜਿਹੇ ਹੁੰਦੇ ਹਨ।[31]

ਬੁਧ ਅਤੇ ਸ਼ੁੱਕਰ ਨੂੰ ਸੰਭਵ ਤੌਰ ਉੱਤੇ ਸੂਰਜ ਦੇ ਜਵਾਰ-ਭਾਟਾ ਦੇ ਵਿਗਾਡ਼ ਦੁਆਰਾ ਸਥਿਰ ਕੀਤਾ ਗਿਆ ਹੈ। ਜਿਵੇਂ ਕਿ ਉੱਪਰ ਦੱਸਿਆ ਗਿਆ ਹੈ, ਧਰਤੀ ਨੂੰ ਚੰਦਰਮਾ ਦੁਆਰਾ ਸਥਿਰ ਕੀਤਾ ਗਿਆ ਸੀ, ਪਰ ਇਸ ਦੇ ਬਣਨ ਤੋਂ ਪਹਿਲਾਂ, ਧਰਤੀ ਵੀ ਅਸਥਿਰਤਾ ਦੇ ਸਮੇਂ ਵਿੱਚੋਂ ਲੰਘ ਸਕਦੀ ਸੀ। ਮੰਗਲ ਦੀ ਤਿਰਛੀਤਾ ਲੱਖਾਂ ਸਾਲਾਂ ਤੋਂ ਕਾਫ਼ੀ ਪਰਿਵਰਤਨਸ਼ੀਲ ਹੈ ਅਤੇ ਇਹ ਇੱਕ ਹਫਡ਼ਾ-ਦਫਡ਼ੀ ਵਾਲੀ ਸਥਿਤੀ ਵਿੱਚ ਹੋ ਸਕਦੀ ਹੈ-ਇਹ ਗ੍ਰਹਿਆਂ ਦੇ ਗਡ਼ਬਡ਼ੀ ਦੇ ਅਧਾਰ ਤੇ ਕੁਝ ਲੱਖਾਂ ਸਾਲ ਵਿੱਚ 0 ° ਤੋਂ 60 ° ਤੱਕ ਬਦਲਦੀ ਹੈ।[25][32] ਕੁਝ ਲੇਖਕ ਇਸ ਗੱਲ ਉੱਤੇ ਵਿਵਾਦ ਕਰਦੇ ਹਨ ਕਿ ਮੰਗਲ ਦੀ ਤਿਰਛੀਤਾ ਹਫਡ਼ਾ-ਦਫਡ਼ੀ ਵਾਲੀ ਹੈ, ਅਤੇ ਇਹ ਦਰਸਾਉਂਦੀ ਹੈ ਕਿ ਜਵਾਰਾਂ ਦਾ ਵਿਗਾਡ਼ ਅਤੇ ਲੇਸਦਾਰ ਕੋਰ-ਮੈਂਟਲ ਕਪਲਿੰਗ ਇਸ ਲਈ ਕਾਫ਼ੀ ਹਨ ਕਿ ਇਹ ਬੁੱਧ ਅਤੇ ਸ਼ੁੱਕਰ ਦੇ ਸਮਾਨ ਪੂਰੀ ਤਰ੍ਹਾਂ ਡੈਂਪਡ ਅਵਸਥਾ ਵਿੱਚ ਪਹੁੰਚ ਗਿਆ ਹੈ।[3][33]

ਮੰਗਲ ਦੇ ਐਕਸੀਅਲ ਝੁਕਾਅ ਵਿੱਚ ਕਦੇ-ਕਦਾਈਂ ਤਬਦੀਲੀਆਂ ਨੂੰ ਮੰਗਲ ਦੀ ਹੋਂਦ ਦੇ ਦੌਰਾਨ ਨਦੀਆਂ ਅਤੇ ਝੀਲਾਂ ਦੀ ਦਿੱਖ ਅਤੇ ਅਲੋਪ ਹੋਣ ਦੀ ਵਿਆਖਿਆ ਵਜੋਂ ਸੁਝਾਅ ਦਿੱਤਾ ਗਿਆ ਹੈ। ਇੱਕ ਤਬਦੀਲੀ ਵਾਯੂਮੰਡਲ ਵਿੱਚ ਮੀਥੇਨ ਦੇ ਫਟਣ ਦਾ ਕਾਰਨ ਬਣ ਸਕਦੀ ਹੈ, ਜਿਸ ਨਾਲ ਗਰਮੀ ਹੋ ਸਕਦੀ ਹੈ, ਪਰ ਫਿਰ ਮੀਥੇਨ ਨਸ਼ਟ ਹੋ ਜਾਵੇਗੀ ਅਤੇ ਮੌਸਮ ਦੁਬਾਰਾ ਸੁੱਕਾ ਹੋ ਜਾਵੇਗਾ।[34][35]

ਬਾਹਰੀ ਗ੍ਰਹਿਆਂ ਦੀਆਂ ਤਿਰਛੀ ਸਥਿਤੀਆਂ ਨੂੰ ਮੁਕਾਬਲਤਨ ਸਥਿਰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ।

ਚੁਣੇ ਹੋਏ ਸੂਰਜੀ ਸਿਸਟਮ ਦੇ ਸਰੀਰਾਂ ਦਾ ਧੁਰਾ ਅਤੇ ਘੁੰਮਣ
ਸਰੀਰ ਨਾਸਾ, ਜੇ2000.0 ਯੁਗ[36] IAU, 0h 0 ਜਨਵਰੀ 2010 TT epoch[37]
ਐਕਸੀਅਲ ਝੁਕਣਾ (ਡਿਗਰੀ)
ਉੱਤਰੀ ਧਰੁਵ ਰੋਟੇਸ਼ਨਲ ਪੀਰੀਅਡ (ਘੰਟੇ)

ਐਕਸੀਅਲ ਝੁਕਣਾ (ਡਿਗਰੀ)
ਉੱਤਰੀ ਧਰੁਵ ਘੁੰਮਾਉਣਾ (ID1)
ਆਰ. ਏ. (ਡਿਗਰੀ) ਦਸੰਬਰ (ਡਿਗਰੀ) ਆਰ. ਏ. (ਡਿਗਰੀ) ਦਸੰਬਰ (ਡਿਗਰੀ)
ਸੂਰਜ 7.25 286.13 63.87 609.12 [upper-alpha 1] 7. 25 [upper-alpha 2] 286.15 63.89 14.18
ਪਾਰਾ 0.03 281.01 61.41 1407.6 0.01 281.01 61.45 6.14
ਵੀਨਸ 2.64 272.76 67.16 −5832.6 2.64 272.76 67.16 −1.48
ਧਰਤੀ 23.44 0.00 90.00 23.93 23.44 Undefined 90.00 360.99
ਚੰਦਰਮਾ 6.68 - - 655.73 54 [ਉੱਪਰ-ਅਲਫ਼ਾ 3][upper-alpha 3] 270.00 66.54 13.18
ਮੰਗਲ 25.19 317.68 52.89 24.62 25.19 317.67 52.88 350.89
ਜੁਪੀਟਰ 3.13 268.06 64.50 9. 93 [upper-alpha 4] 3.12 268.06 64.50 870.54 [upper-alpha 4]
ਸੈਟਰਨ 26.73 40.59 83.54 10.66 [upper-alpha 4] 26.73 40.59 83.54 810.79 [upper-alpha 4]
ਯੂਰੇਨਸ 82.23 257.31 −15.18 - 17.24 [upper-alpha 4] 82.23 257.31 −15.18 - 501.16 [upper-alpha 4]
ਨੇਪਚੂਨ 28.32 299.33 42.95 16.11 [upper-alpha 4] 28.33 299.40 42.95 536.31 [upper-alpha 4]
ਪਲੂਟੋ[upper-alpha 5] 57.47 312.99 [ਉੱਪਰ-ਅਲਫ਼ਾ 5][upper-alpha 5] 6. 16 [upper-alpha 5] −153.29 60.41 312.99 6.16 −56.36
  1. ↑ At 16° latitude; the Sun's rotation varies with latitude.
  2. ↑ With respect to the ecliptic of 1850.
  3. ↑ With respect to the ecliptic; the Moon's orbit is inclined 5.16° to the ecliptic.
  4. ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 From the origin of the radio emissions; the visible clouds generally rotate at different rate.
  5. ↑ 5.0 5.1 5.2 NASA lists the coordinates of Pluto's positive pole; noted values have been reinterpreted to correspond to the north/negative pole.

ਬਾਹਰੀ ਗ੍ਰਹਿ

[ਸੋਧੋ]

ਤਾਰਿਆਂ ਦਾ ਧੁਰੀ ਝੁਕਾਉ ψs, ਅਰਥਾਤ ਕਿਸੇ ਤਾਰੇ ਦਾ ਇਸ ਦੇ ਕਿਸੇ ਗ੍ਰਹਿ ਦੇ ਚੱਕਰਵਰਤੀ ਤਲ ਦੇ ਸੰਬੰਧ ਵਿੱਚ ਧੁਰੇ ਦਾ ਝੁਕਾਅ, ਸਿਰਫ ਕੁਝ ਪ੍ਰਣਾਲੀਆਂ ਲਈ ਨਿਰਧਾਰਤ ਕੀਤਾ ਗਿਆ ਹੈ। 2012 ਤੱਕ, 49 ਤਾਰਿਆਂ ਵਿੱਚ ਅਸਮਾਨ-ਪ੍ਰੋਜੈਕਟ ਸਪਿਨ-ਔਰਬਿਟ ਗਲਤ ਸੰਰਚਨਾ λ ਵੇਖੀ ਗਈ ਹੈ, ਜੋ ψs ਦੀ ਇੱਕ ਘੱਟ ਸੀਮਾ ਦੇ ਰੂਪ ਵਿੱਚ ਕੰਮ ਕਰਦੀ ਹੈ।[38] ਇਹਨਾਂ ਮਾਪ ਵਿੱਚੋਂ ਜ਼ਿਆਦਾਤਰ ਰੋਸੀਟਰ-ਮੈਕਲੌਗਲਿਨ ਪ੍ਰਭਾਵ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦੇ ਹਨ। ਕੇਪਲਰ ਪੁਲਾਡ਼ ਦੂਰਬੀਨ ਵਰਗੇ ਪੁਲਾਡ਼-ਅਧਾਰਤ ਦੂਰਬੀਨਾਂ ਦੇ ਲਾਂਚ ਤੋਂ ਬਾਅਦ, ਕਿਸੇ ਬਾਹਰੀ ਗ੍ਰਹਿ ਦੀ ਤਿਰਛੀਤਾ ਨੂੰ ਨਿਰਧਾਰਤ ਕਰਨਾ ਅਤੇ ਅਨੁਮਾਨ ਲਗਾਉਣਾ ਸੰਭਵ ਹੋ ਗਿਆ ਹੈ। ਗ੍ਰਹਿ ਦਾ ਘੁੰਮਣ-ਫਿਰਨ ਵਾਲਾ ਸਮਤਲ ਹੋਣਾ ਅਤੇ ਚੰਦਰਮਾ ਅਤੇ/ਜਾਂ ਰਿੰਗਾਂ ਦਾ ਦਲ, ਜੋ ਉੱਚ-ਸ਼ੁੱਧਤਾ ਫੋਟੋਮੈਟਰੀ ਨਾਲ ਖੋਜਣਯੋਗ ਹਨ, ਗ੍ਰਹਿ ਤਿਰਛੀਤਾ, ψp ਤੱਕ ਪਹੁੰਚ ਪ੍ਰਦਾਨ ਕਰਦੇ ਹਨ। ਇਸ ਤੋਂ ਬਾਅਦ ਬਹੁਤ ਸਾਰੇ ਬਾਹਰੀ ਗ੍ਰਹਿਆਂ ਨੇ ਆਪਣੀ ਤਿਰਛੀਤਾ ਨਿਰਧਾਰਤ ਕੀਤੀ ਹੈ, ਜਿਵੇਂ ਕਿ ਕੇਪਲਰ-186f ਅਤੇ ਕੇਪਲਰ-413b।[39][40]

ਖਗੋਲ-ਵਿਗਿਆਨੀਆਂ ਨੇ ਬਾਹਰੀ ਗ੍ਰਹਿਆਂ ਦੀ ਤਿਰਛੀਤਾ ਦੀ ਭਵਿੱਖਬਾਣੀ ਕਰਨ ਲਈ ਜਵਾਰ-ਭਾਟਾ ਸਿਧਾਂਤਾਂ ਨੂੰ ਲਾਗੂ ਕੀਤਾ ਹੈ। ਇਹ ਦਿਖਾਇਆ ਗਿਆ ਹੈ ਕਿ ਘੱਟ ਪੁੰਜ ਵਾਲੇ ਤਾਰਿਆਂ ਦੇ ਆਲੇ ਦੁਆਲੇ ਰਹਿਣ ਯੋਗ ਖੇਤਰ ਵਿੱਚ ਐਕਸੋਪਲੈਨੇਟਸ ਦੀਆਂ ਤਿਰਛੀਤਾ 109 ਸਾਲਾਂ ਤੋਂ ਵੀ ਘੱਟ ਸਮੇਂ ਵਿੱਚ ਖਤਮ ਹੋ ਜਾਂਦੀਆਂ ਹਨ, ਜਿਸਦਾ ਅਰਥ ਹੈ ਕਿ ਉਨ੍ਹਾਂ ਕੋਲ ਝੁਕਣ ਵਾਲੇ ਮੌਸਮ ਨਹੀਂ ਹੋਣਗੇ ਜਿਵੇਂ ਕਿ ਧਰਤੀ ਹੈ.[41][42]

ਹਵਾਲੇ

[ਸੋਧੋ]
  1. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000004D-QINU`"'</ref>" does not exist.
  2. ↑ Explanatory Supplement 1992, p. 384
  3. ↑ 3.0 3.1 Correia, Alexandre C. M.; Laskar, Jacques; de Surgy, Olivier Néron (May 2003). "Long-term evolution of the spin of Venus I. theory" (PDF). Icarus. 163 (1): 1–23. Bibcode:2003Icar..163....1C. doi:10.1016/S0019-1035(03)00042-3. Archived from the original (PDF) on 9 October 2022. ਹਵਾਲੇ ਵਿੱਚ ਗ਼ਲਤੀ:Invalid <ref> tag; name "CorreiaVenusI" defined multiple times with different content
  4. ↑ Correia, A. C. M.; Laskar, J. (2003). "Long-term evolution of the spin of Venus: II. numerical simulations" (PDF). Icarus. 163 (1): 24–45. Bibcode:2003Icar..163...24C. doi:10.1016/S0019-1035(03)00043-5. Archived from the original (PDF) on 9 October 2022.
  5. ↑ Seidelmann, P. Kenneth; Archinal, B. A.; a'Hearn, M. F.; Conrad, A.; Consolmagno, G. J.; Hestroffer, D.; Hilton, J. L.; Krasinsky, G. A.; Neumann, G. (2007). "Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements: 2006". Celestial Mechanics and Dynamical Astronomy. 98 (3): 155–180. Bibcode:2007CeMDA..98..155S. doi:10.1007/s10569-007-9072-y.
  6. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000052-QINU`"'</ref>" does not exist.
  7. ↑ "Glossary" in Astronomical Almanac Online. (2023). Washington DC: United States Naval Observatory. s.v. obliquity.
  8. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000053-QINU`"'</ref>" does not exist.
  9. ↑ Ray, Richard D.; Erofeeva, Svetlana Y. (4 February 2014). "Long-period tidal variations in the length of day". Journal of Geophysical Research: Solid Earth. 119 (2): 1498–1509. Bibcode:2014JGRB..119.1498R. doi:10.1002/2013JB010830.
  10. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000055-QINU`"'</ref>" does not exist.
  11. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000056-QINU`"'</ref>" does not exist.
  12. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000057-QINU`"'</ref>" does not exist.
  13. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000058-QINU`"'</ref>" does not exist.
  14. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-00000059-QINU`"'</ref>" does not exist.
  15. ↑ Dreyer (1890), p. 123
  16. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000005A-QINU`"'</ref>" does not exist.
  17. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000005B-QINU`"'</ref>" does not exist.
  18. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000005C-QINU`"'</ref>" does not exist.
  19. ↑ Astronomical Almanac 2010, p. B52
  20. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000005D-QINU`"'</ref>" does not exist.
  21. ↑ Explanatory Supplement (1961), sec. 2C
  22. ↑ "Basics of Space Flight, Chapter 2". Jet Propulsion Laboratory/NASA. 29 October 2013. Retrieved 26 March 2015.
  23. ↑ Nakli itihaas jo likheya geya hai kade na vaapriya jo ohna de base te, saade te saada itihaas bna ke ehna ne thop dittiyan. anglo sikh war te ek c te 3-4 jagaha te kiwe chal rahi c ikko war utto saal 1848 jdo angrej sara punjab 1845 ch apne under kar chukke c te oh 1848 ch kihna nal jang ladd rahe c. Script error: The function "citation198.168.27.221 14:54, 13 ਦਸੰਬਰ 2024 (UTC)'"`UNIQ--ref-0000005F-QINU`"'</ref>" does not exist.
  24. ↑ Berger, A.L. (1976). "Obliquity and Precession for the Last 5000000 Years". Astronomy and Astrophysics. 51 (1): 127–135. Bibcode:1976A&A....51..127B.
  25. ↑ 25.0 25.1 Laskar, J.; Robutel, P. (1993). "The Chaotic Obliquity of the Planets" (PDF). Nature. 361 (6413): 608–612. Bibcode:1993Natur.361..608L. doi:10.1038/361608a0. Archived from the original (PDF) on 23 November 2012. ਹਵਾਲੇ ਵਿੱਚ ਗ਼ਲਤੀ:Invalid <ref> tag; name "LaskarRobutel" defined multiple times with different content
  26. ↑ Laskar, J.; Joutel, F.; Robutel, P. (1993). "Stabilization of the Earth's Obliquity by the Moon" (PDF). Nature. 361 (6413): 615–617. Bibcode:1993Natur.361..615L. doi:10.1038/361615a0. Archived from the original (PDF) on 9 October 2022.
  27. ↑ Lissauer, J.J.; Barnes, J.W.; Chambers, J.E. (2011). "Obliquity variations of a moonless Earth" (PDF). Icarus. 217 (1): 77–87. Bibcode:2012Icar..217...77L. doi:10.1016/j.icarus.2011.10.013. Archived from the original (PDF) on 8 June 2013.
  28. ↑ Li, Gongjie; Batygin, Konstantin (20 July 2014). "On the Spin-axis Dynamics of a Moonless Earth". Astrophysical Journal. 790 (1): 69–76. arXiv:1404.7505. Bibcode:2014ApJ...790...69L. doi:10.1088/0004-637X/790/1/69.
  29. ↑ Ward, W.R. (1982). "Comments on the Long-Term Stability of the Earth's Obliquity". Icarus. 50 (2–3): 444–448. Bibcode:1982Icar...50..444W. doi:10.1016/0019-1035(82)90134-8.
  30. ↑ Berger, 1976.
  31. ↑ 31.0 31.1 William Ward (20 July 1973). "Large-Scale Variations in the Obliquity of Mars". Science. 181 (4096): 260–262. Bibcode:1973Sci...181..260W. doi:10.1126/science.181.4096.260. PMID 17730940.
  32. ↑ Touma, J.; Wisdom, J. (1993). "The Chaotic Obliquity of Mars" (PDF). Science. 259 (5099): 1294–1297. Bibcode:1993Sci...259.1294T. doi:10.1126/science.259.5099.1294. PMID 17732249. Archived from the original (PDF) on 25 June 2010.
  33. ↑ Correia, Alexandre C.M; Laskar, Jacques (2009). "Mercury's capture into the 3/2 spin-orbit resonance including the effect of core-mantle friction". Icarus. 201 (1): 1–11. arXiv:0901.1843. Bibcode:2009Icar..201....1C. doi:10.1016/j.icarus.2008.12.034.
  34. ↑ Rebecca Boyle (7 October 2017). "Methane burps on young Mars helped it keep its liquid water". New Scientist.
  35. ↑ Edwin Kite (2 October 2017). "Methane bursts as a trigger for intermittent lake-forming climates on post-Noachian Mars" (PDF). Nature Geoscience. 10 (10): 737–740. arXiv:1611.01717. Bibcode:2017NatGe..10..737K. doi:10.1038/ngeo3033. Archived from the original (PDF) on 23 July 2018. {{cite journal}}: Unknown parameter |displayauthors= ignored (|display-authors= suggested) (help)
  36. ↑ Planetary Fact Sheets, at http://nssdc.gsfc.nasa.gov
  37. ↑ Astronomical Almanac 2010, pp. B52, C3, D2, E3, E55
  38. ↑ Heller, R. "Holt-Rossiter-McLaughlin Encyclopaedia". René Heller. Retrieved 24 February 2012.
  39. ↑ Grossman, David (2018-06-29). "Study Shows Exoplanet Has a Stable Axis Just Like Earth". Popular Mechanics (in ਅੰਗਰੇਜ਼ੀ (ਅਮਰੀਕੀ)). Retrieved 2024-02-26.
  40. ↑ "Kepler Finds a Very Wobbly Planet - NASA" (in ਅੰਗਰੇਜ਼ੀ (ਅਮਰੀਕੀ)). 2014-02-04. Retrieved 2024-02-26.
  41. ↑ Heller, R.; Leconte, J.; Barnes, R. (2011). "Tidal obliquity evolution of potentially habitable planets". Astronomy and Astrophysics. 528: A27. arXiv:1101.2156. Bibcode:2011A&A...528A..27H. doi:10.1051/0004-6361/201015809.
  42. ↑ Heller, R.; Leconte, J.; Barnes, R. (2011). "Habitability of Extrasolar Planets and Tidal Spin Evolution". Origins of Life and Evolution of Biospheres. 41 (6): 539–43. arXiv:1108.4347. Bibcode:2011OLEB...41..539H. doi:10.1007/s11084-011-9252-3. PMID 22139513.
ਹਵਾਲੇ ਵਿੱਚ ਗ਼ਲਤੀ:<ref> tag defined in <references> has no name attribute.

ਬਾਹਰੀ ਲਿੰਕ

[ਸੋਧੋ]
"https://pa.wikipedia.org/w/index.php?title=ਧਰੂਵੀ_ਝੁਕਾਅ&oldid=768616" ਤੋਂ ਲਿਆ